Analysis of high-gamma band signals in human ECoG
Introduction
In this example script, we will demonstrate how to analyze functional brain activity in ECoG data. The tutorial contains instructions and code for event-related potentials (ERP), high-gamma power (HGP, 80 - 200 Hz) and time-frequency analyses, including statistical analyses and visualization of the outcome. HGP is a measure of neural activity that is specific for ECoG data analysis. Because high frequency signals are strongly attenuated by tissue and bone that lie between source and sensor, high-gamma activity can hardly be found in scalp EEG data. However, in ECoG data HGP (80 - 200 Hz) is a very prominent neural signature. HGP does not seem to be of oscillatory nature but has rather been associated with population neural spiking rate (Manning et al., 2009; Ray & Maunsell, 2011). It is also highly locally specific, compared with low frequency activity and ERPs.
Background
This dataset was recorded at the Comprehensive Epilepsy Center of the New York University School of Medicine and processed by members of the Clinical Neurophysiology Lab (Thomas Thesen) and the Multisensory Integration Research Group (Martin Krebber, Daniel Senkowski, Charité - University Medicine Berlin). (Support by the CRCNS Data Sharing Grant 01GQ1416 is gratefully acknowledged.) This dataset includes neural recordings from an electrode grid, with an experimental manipulation that illustrates the spatiotemporal precision of these type of recordings. We will repeat code to select the trials and preprocess the data as described in the time-frequency analysis tutorial. We assume that the reader is already familiar with preprocessing and time-frequency analysis.
The patient suffered from intractable epilepsy and underwent invasive monitoring to localize the epileptogenic zone for subsequent surgical removal. Electrode placement was solely guided by clinical considerations. During the recording the patient performed a visual localizer task that was used to identify electrodes responsive to certain types of visual input. Stimuli from the following 7 categories were presented in random order (event codes in parentheses): false font (3), house (4), object (5), texture (6), body (7), text (8), face (9).
The data SubjectNY394.zip can be downloaded from our download server.
Data analysis
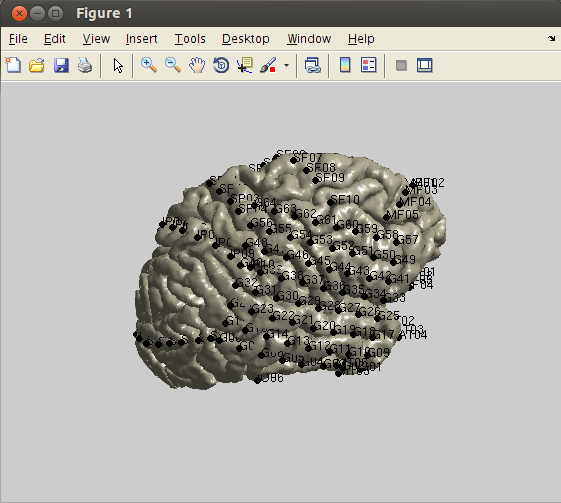
In line with the main tutorial, you can use the following code for surface rendering and the plotting of electrodes. Note that in this dataset many steps are skipped and we are just plotting the result of the anatomical coregistration and electrode placement.
%% load electrode locations
fid = fopen('NY394_MRI_coor.txt');
elec_info = textscan(fid,'%s %f %f %f %s');
fclose(fid);
% create FieldTrip electrode structure
% elec = [];
elec.label = elec_info{1};
elec.elecpos = [elec_info{2} elec_info{3} elec_info{4}];
elec.unit = 'mm';
%% load pial surface
load('NY394_MRI_rh_pial_surface.mat');
% create FieldTrip surface mesh structure
mesh = [];
mesh.pos = surface.pos;
mesh.tri = surface.tri;
mesh.unit = 'mm';
%% plot surface and electrodes
ft_plot_mesh(mesh, 'facecolor', [0.781 0.762 0.664], 'EdgeColor', 'none')
view([90 25])
lighting gouraud
material shiny
camlight
% plot electrodes
hs = ft_plot_sens(elec, 'style', 'ko', 'label', 'on');
set(hs, 'MarkerFaceColor', 'k', 'MarkerSize', 6);
1. Data preprocessing
First, we will load the data and segment them into trials using ft_preprocessing. Event information has already been extracted from the trigger channels and stored in NY394_trl.mat. The segmentation of continuous data based on triggers is described in detail in one of the preprocessing tutorials.
% load trial info
load('NY394_trl.mat');
% load and segment data
cfg = [];
cfg.dataset = 'NY394_VisualLoc_R1.edf';
cfg.trl = trl; % from NY394_trl.mat
cfg.continuous = 'yes';
epoch_data = ft_preprocessing(cfg);
The data still contain some channels that are not required for the further analysis (e.g., ‘Pulse’ and ‘ECG’ channels). We will use ft_selectdata to select only channels that have the ‘EEG’ prefix. Only these data will be submitted to subsequent analysis steps.
cfg = [];
cfg.channel = 'EEG*'; % select 'EEG' channles
epoch_data = ft_selectdata(cfg,epoch_data);
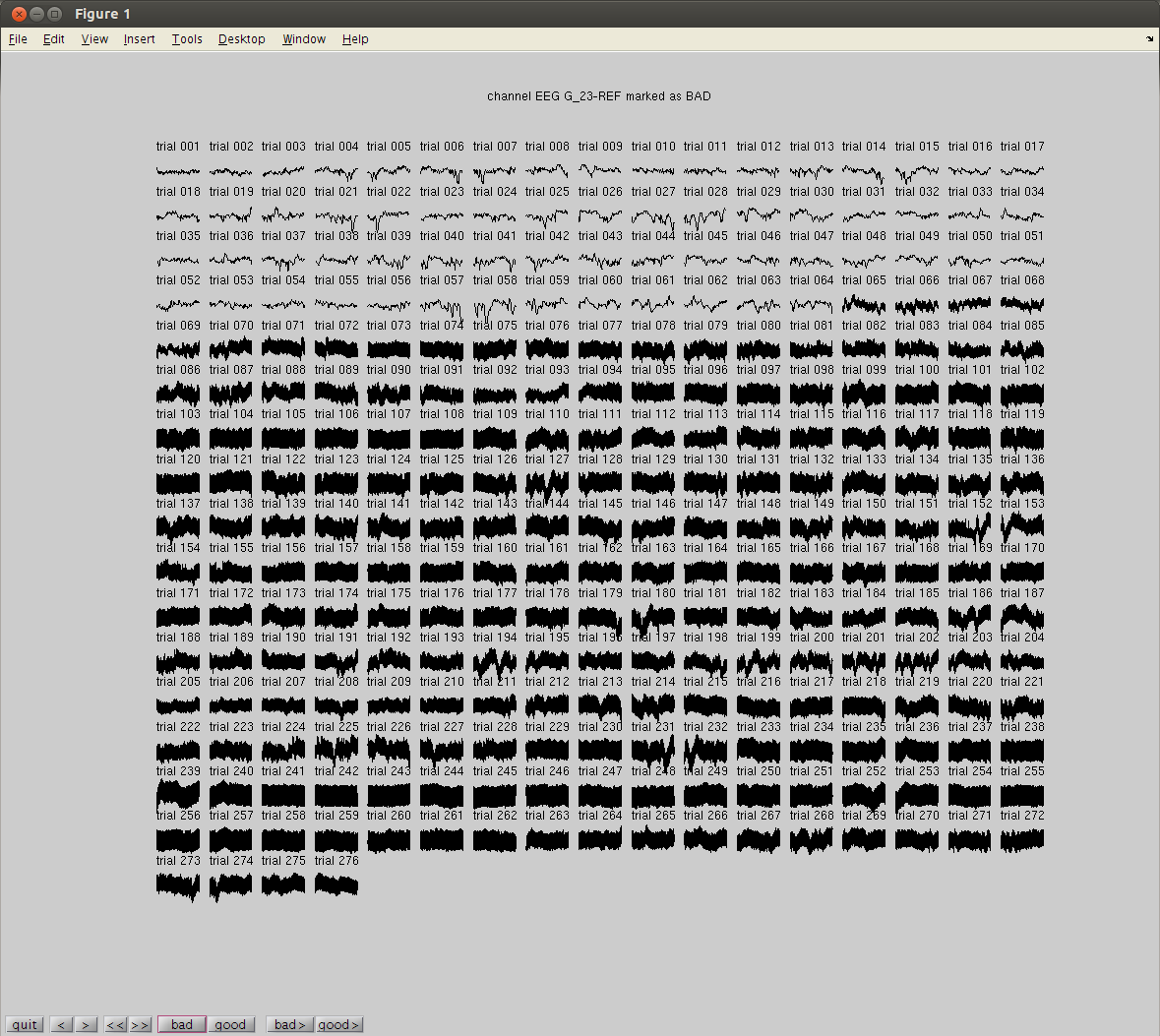
Artifact rejection can be done by visually inspecting individual trials and channels, or by using summary statistics that are calculated across trials and channels (see tutorial here). We will first visually reject bad channels by browsing through the data channel-wise using ft_rejectvisual with the method ‘channel’. You will notice that the data from channel 23 appear very noisy after about a quarter of trials. This is probably a technical artifact due to a bad electrode contact. Therefore, the channel should be marked as bad.
cfg = [];
cfg.method = 'channel'; % browse through channels
cfg.channel = 'all';
epoch_data_clean_chan = ft_rejectvisual(cfg, epoch_data);
For rejecting artifact trials, we will use the ‘summary’ method in ft_rejectvisual. Identifying artifact trials in ECoG is similar to EEG analysis and can be done according to the tutorial on visual artifact rejection. Note, that ECoG data typically have higher amplitudes and better signal-to-noise ratios compared with data from scalp EEG, because they are recorded directly from the cortex. Still, a number of technical and physiological artifacts can be present in the data. Due to the clinical - and therefore less rigorously controlled - environment during the recording process, technical artifacts are quite common. The present dataset is relatively clean and, hence, does not need much rejection. Some moderate outliers can be found for the metrics: maxabs, zvalue and maxzvalue.
cfg = [];
cfg.method = 'summary'; % summary statistics across channels and trials
cfg.channel = 'all';
epoch_data_clean = ft_rejectvisual(cfg, epoch_data_clean_chan);
2. Re-reference the data
FIXME
3. ERP and HGP analysis
3.1 calculate and plot ERPs
The analysis of event-related potentials is done in accordance with the standard ERP tutorial. Here, we will calculate and compare the ERPs of two conditions (‘object’ and ‘face’). In the parameters of ft_timelockanalysis we use the preprocessing options to apply filters to the data (30 Hz low-pass, 1 Hz high-pass). The high-pass filter reduces slow drifts while the low-pass filter eliminates high-frequency noise. Note that the exact filter setting depends on the ERP component under investigation. Baseline correction is subsequently done with respect to the time interval of -300 ms to - 50 ms.
% calculate ERPs
cfg = [];
cfg.keeptrials = 'yes'; % keep trials for statistics
cfg.preproc.lpfilter = 'yes';
cfg.preproc.lpfreq = 30; % smooth ERP with low-pass filter
cfg.preproc.hpfilter = 'yes';
cfg.preproc.hpfreq = 1; % reduce slow drifts
cfg.preproc.detrend = 'yes';
cfg.trials = find(epoch_data_clean.trialinfo == 3); % select only 'object' trials (event code 3)
ERP_object = ft_timelockanalysis(cfg, epoch_data_clean);
cfg.trials = find(epoch_data_clean.trialinfo == 7); % select only 'face' trials (event code 7)
ERP_face = ft_timelockanalysis(cfg, epoch_data_clean);
% baseline correction
cfg = [];
cfg.baseline = [-.3 -.05];
ERP_object_bl = ft_timelockbaseline(cfg,ERP_object);
ERP_face_bl = ft_timelockbaseline(cfg,ERP_face);
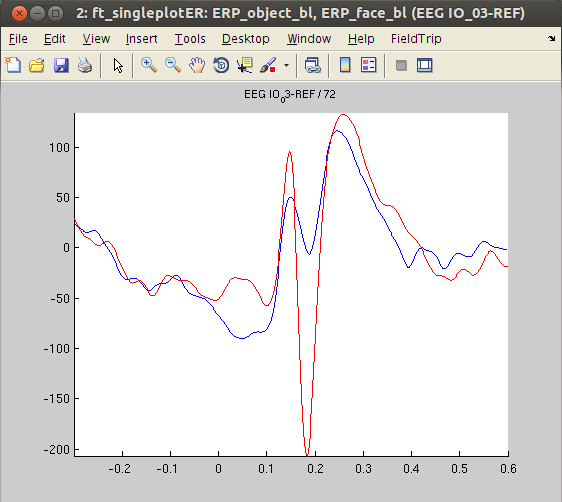
For plotting the data we select channel ‘IO_03’, located in or in close proximity of the fusiform face area, which is known to strongly respond to face stimuli. In agreement with the literature, the ERPs appear to be larger for ‘face’ compared to ‘object’ stimuli. Before plotting, we need to average the data across trials, because we kept the individual trials when initially calling ft_timelockanalysis.
cfg = [];
cfg.avgoverrpt = 'yes';
ERP_object_avg = ft_selectdata(cfg, ERP_object_bl);
ERP_face_avg = ft_selectdata(cfg, ERP_face_bl);
cfg = [];
cfg.parameter = 'trial';
cfg.xlim = [-.3 .6];
cfg.channel = 'EEG IO_03-REF'; % other responsive channels: 'EEG PT_04-REF', 'EEG IO_02-REF', 'EEG IO_04-REF', 'EEG SO_01-REF', 'EEG SO_02-REF''EEG SO_03-REF'
figure, ft_singleplotER(cfg,ERP_object_avg,ERP_face_avg)
3.2 calculate and plot HGPs
To calculate HGP, we will first perform ft_freqanalysis over the high-gamma frequency range (80 - 200 Hz). Then, we will manually correct for the 1/f power dropoff and averaged the data over the frequency dimension to get the HGP time course for each channel. The resulting data structure resembles ERP data and can be further processed using ft_timelockxxx functions. Finally, the HGP data are baseline-corrected using ft_timelockbaseline.
% time-frequency analysis
cfg = [];
cfg.method = 'tfr';
cfg.keeptrials = 'yes';
cfg.toi = epoch_data_clean.time{1}; % keep full temporal resolution
cfg.foi = [80 85 90 95 100 105 110 115 125 130 135 140 145 150 155 160 165 170 175 185 190]; % 80 - 190 Hz, leave out harmonics of 60 Hz
cfg.width = 10 * ones(1,length(cfg.foi));
cfg.trials = find(epoch_data_clean.trialinfo == 3); % select 'object' trials
TFR_object = ft_freqanalysis(cfg,epoch_data_clean);
cfg.trials = find(epoch_data_clean.trialinfo == 7); % select 'face' trials
TFR_face = ft_freqanalysis(cfg,epoch_data_clean);
% create HGP as empty timelock structure with same dimensions as ERP, values will be filled in in the next steps
HGP_object = rmfield(ERP_object,{'trial'});
HGP_face = rmfield(ERP_face,{'trial'});
% correct for the 1/f dropoff
freqcorr = reshape(TFR_object.freq.^2,[1 1 length(TFR_object.freq)]); %this vector accounts for the 1/f dropoff
% use repmat to create a matrix the same size as the TFR data
freqcorr_object = repmat(freqcorr,[size(TFR_object.powspctrm,1) size(TFR_object.powspctrm,2) 1 length(TFR_object.time)]);
freqcorr_face = repmat(freqcorr,[size(TFR_face.powspctrm,1) size(TFR_face.powspctrm,2) 1 length(TFR_face.time)]);
% multiply data with freqcorr matrix and average over frequencies
HGP_object.trial = squeeze(nanmean(TFR_object.powspctrm(:,:,:,:) .* freqcorr_object,3));
HGP_face.trial = squeeze(nanmean(TFR_face.powspctrm(:,:,:,:) .* freqcorr_face,3));
% baseline correction
cfg = [];
cfg.baseline = [-.3 -.05];
HGP_object_bl = ft_timelockbaseline(cfg,HGP_object);
HGP_face_bl = ft_timelockbaseline(cfg,HGP_face);
clear TFR*
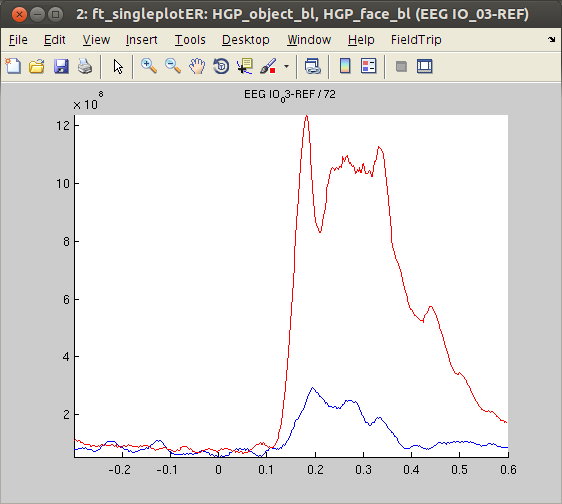
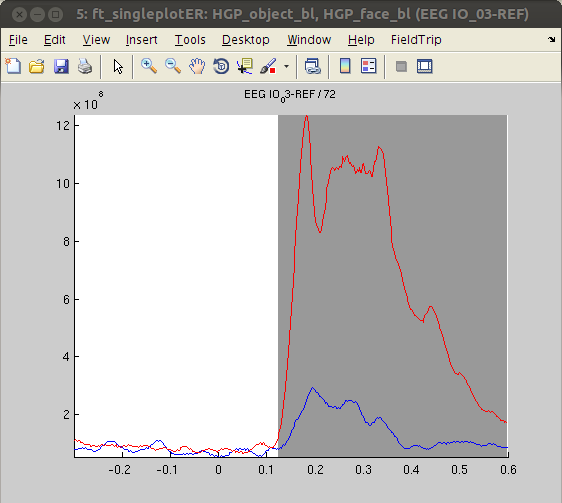
Again, we decided to plot channel ‘IO_03’. As was the case for the ERPs, the HGP response at this channel was larger for ‘face’ stimuli than ‘object’ stimuli.
cfg = [];
cfg.xlim = [-.3 .6];
cfg.channel = 'EEG IO_03-REF'; % other responsive channels: 'EEG PT_03-REF', 'EEG PT_04-REF', 'EEG IO_02-REF', 'EEG IO_04-REF', 'EEG SO_01-REF', 'EEG SO_02-REF''EEG SO_03-REF'
figure, ft_singleplotER(cfg,HGP_object_bl,HGP_face_bl)
3.3 calculate timelock statistics
In the next analysis step, we statistically compare the responses of ‘objects’ vs. ‘faces’ for both ERP and HGP data to test which electrodes respond preferentially to one or the other stimulus class. To account for multiple comparisons, we use the cluster-based permutation approach as implemented in ft_timelockstatistics. When it comes to statistics, one distinctive feature of ECoG data is that, due to the high local specificity of the recorded activity, no spatial information is exploited for clustering. Consequently, the cfg.neighbours parameter is specified as an empty matrix.
cfg = [];
cfg.latency = [0 .6];
cfg.parameter = 'trial';
cfg.method = 'montecarlo';
cfg.correctm = 'cluster';
cfg.neighbours = []; % no spatial information is exploited for statistical clustering
cfg.numrandomization = 500;
cfg.statistic = 'indepsamplesT'; % idependent samples test for statistical testing on the single-trial level
cfg.channel = 'all';
cfg.alpha = 0.05;
cfg.correcttail = 'alpha';
cfg.design = [ones(1,size(ERP_object_bl.trial,1)), 2*ones(1,size(ERP_face_bl.trial,1))];
stats_ERP = ft_timelockstatistics(cfg,ERP_object_bl,ERP_face_bl);
stats_HGP = ft_timelockstatistics(cfg,HGP_object_bl,HGP_face_bl);
We first check whether the cluster statistic revealed significant channels. If there are significant channels, we will plot them.
% look for significant channels in ERP stats
[chans time] = find(stats_ERP.mask)
% none of the channels contain significant differences between conditions
Although the visual inspection of the data indicated stronger ERP responses for ‘face’ stimuli in an electrode near the fusiform face area, the statistical analysis of ERPs did not reveal significant effects at any channel. Thus, we move on to the statistics of the HGP data.
% look for significant channels in HGP stats
[chans time] = find(stats_HGP.mask);
chans = unique(chans)
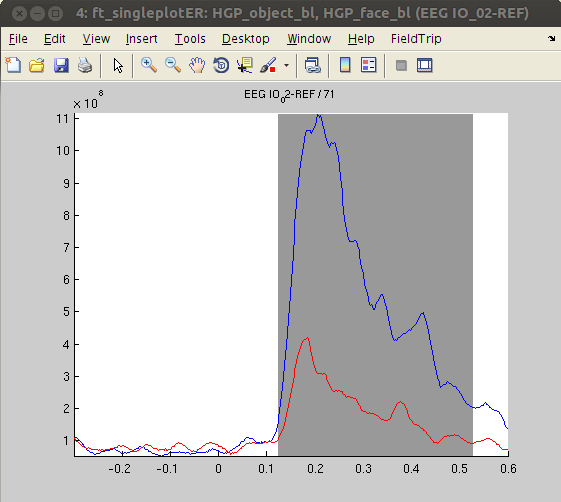
There are six channels with significantly different HGP time courses when comparing the ‘objects’ and ‘faces’ conditions. We will plot each of these channels using ft_singleplotER.
% first, average over trials, otherwise we'll have problems with ft_singleplotER
cfg = [];
HGP_object_bl = ft_timelockanalysis(cfg, HGP_object_bl)
HGP_face_bl = ft_timelockanalysis(cfg, HGP_face_bl)
% add statistical mask to data
time_idx = find(HGP_object_bl.time == stats_HGP.time(1)) : find(HGP_object_bl.time == stats_HGP.time(end)); % find indices of timepoints in data corresponding to timepoints in stats
HGP_object_bl.mask = false(size(HGP_object_bl.avg));
HGP_object_bl.mask(:,time_idx) = stats_HGP.mask;
% plot the ERP traces
cfg = [];
cfg.parameter = 'avg';
cfg.xlim = [-.3 .6];
cfg.maskparameter = 'mask';
% loop over significant channels and plot
for ichan = 1:length(chans)
cfg.channel = chans(ichan);
figure, ft_singleplotER(cfg,HGP_object_bl,HGP_face_bl),
end
The analysis revealed stronger HGP in response to ‘faces’ compared with ‘objects’ in some channels (IO3, SO2), while other channels show the opposite pattern (PT3, PT6, IO2, SO4). This finding - together with the absence of significant effects in ERPs - suggests that HGP might be more sensitive to the type of visual stimulus presented than ERPs. The results are also in line with the notion that HGP represents highly locally specific activity whereas ERPs and low frequency oscillations are more widespread.
4. Time-frequency analysis
4.1 calculate and plot TFRs
To get an idea about the spectral content in the ECoG dataset, we will calculate time-frequency representations (TFRs) using ft_freqanalysis, and then baseline-correct the data to reflect relative change from baseline using ft_freqbaseline. More information about time-frequency analysis can be found in the time-frequency analysis tutorial). In the current dataset, we decided to analyze the frequency range from 2 to 200 Hz. To save computational resources, we will increase the frequency steps with higher frequencies.
% time-frequency analysis
cfg = [];
cfg.method = 'tfr';
cfg.output = 'pow';
cfg.keeptrials = 'yes'; % keep trials for statistics
cfg.foi = [4:2:40 44:4:100 108:8:200]; % make the frequency spacing broader with higher frequencies
cfg.toi = -.3:.02:.6;
cfg.trials = find(epoch_data_clean.trialinfo==3); % select 'object' trials
TFR_object = ft_freqanalysis(cfg, epoch_data_clean);
cfg.trials = find(epoch_data_clean.trialinfo==7); % select 'face' trials
TFR_face = ft_freqanalysis(cfg, epoch_data_clean);
% baseline correction
cfg = [];
cfg.baseline = [-.3 .05];
cfg.baselinetype ='relchange';
TFR_object_bl = ft_freqbaseline(cfg, TFR_object);
TFR_face_bl = ft_freqbaseline(cfg, TFR_face);
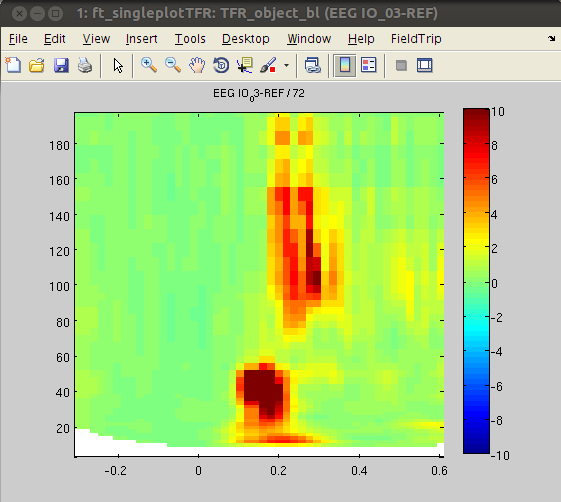
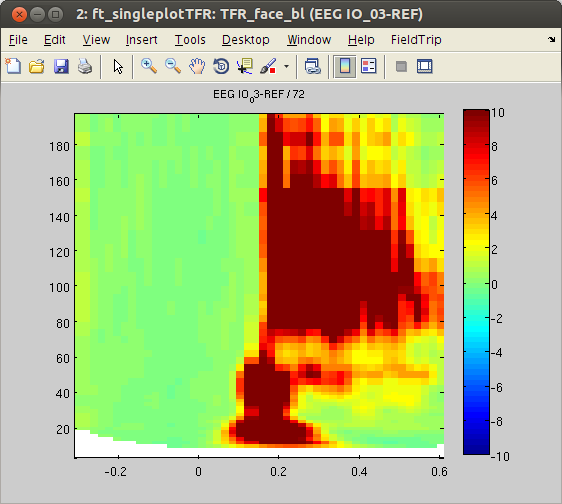
To visualize the time-frequency data from the two conditions, we will plot TFRs for some representative channels using ft_singleplotTFR.
cfg = [];
cfg.parameter = 'powspctrm';
cfg.xlim = [-.3 .6];
cfg.zlim = [-10 10];
cfg.channel = 'EEG IO_03-REF'; % other responsive channels: 'EEG PT_03-REF', 'EEG PT_04-REF', 'EEG IO_02-REF', 'EEG IO_04-REF', 'EEG SO_01-REF', 'EEG SO_02-REF''EEG SO_03-REF'
figure, ft_singleplotTFR(cfg,TFR_object_bl)
figure, ft_singleplotTFR(cfg,TFR_face_bl)
4.2 Time-frequency statistics
In the next step, we statistically compare the TFRs of the ‘house’ and ‘face’ conditions using cluster-based permutation statistics, as implemented in ft_freqstatistics. The statistical approach is presented in more detail in one of the statistics tutorials.
cfg = [];
cfg.latency = [0 .6];
cfg.parameter = 'powspctrm';
cfg.method = 'montecarlo';
cfg.correctm = 'cluster';
cfg.neighbours = [];
cfg.numrandomization = 500;
cfg.statistic = 'indepsamplesT';
cfg.channel = 'all';
cfg.alpha = 0.05;
cfg.correcttail = 'alpha';
cfg.clusteralpha = 0.05;
cfg.design = [ones(1, size(TFR_object_bl.powspctrm,1)), 2*ones(1,size(TFR_face_bl.powspctrm,1))];
cfg.ivar = 1;
stats_TFR = ft_freqstatistics(cfg,TFR_object_bl,TFR_face_bl);
Finally, we will plot the masked t-values from significant channels of the statistical contrast.
% find significant channels
sig_tiles = find(stats_TFR.mask); % find significant time-frequency tiles
[chan freq time] = ind2sub(size(stats_TFR.mask),sig_tiles); % transform linear indices to subscript to extract significant channels, timepoints and frequencies
chan = unique(chan);
% plot TFRs
cfg = [];
cfg.parameter = 'stat';
cfg.maskparameter = 'mask';
cfg.maskalpha = .4; % opacity value for non-significant parts
cfg.zlim = [-4 4];
cfg.colorbar = 'yes';
% loop over channel sets and plot
for ichan = 1:length(chan)
cfg.channel = chan(ichan);
figure, ft_singleplotTFR(cfg,stats_TFR),
end
Similar to the outcome of the HGP analysis, power differences are found in some occipital channels (IO, SO and PT). For instance, channel IO3 responds more strongly to ‘face’ Stimuli, whereas channel IO2 responds more strongly to ‘object’ Stimuli. Notably, the power differences are predominantly found in the high-gamma band range. This suggests that local HGP is highly sensitive for the presented stimulus type.