Whole brain connectivity and network analysis
Introduction
This tutorial will demonstrate one of the possible ways to analyze MEG data from a graph theoretical perspective. It is assumed that you are familiar with the various preprocessing steps which will be performed here, as these are not explained further in detail. An overview and detailed information on preprocessing can be found here and on time-frequency analysis here
This tutorial will use metrics that are derived from graph theory and are implemented in the Brain Connectivity Toolbox (BCT, detailed explanation can be found here).
Background
We will analyze brain activity monitored during a resting condition with eyes closed. In contrast to an event-related analysis where the data is segmented around some external events here we will analyze the entire continuous recording of approximately 5 minutes length.
In general, eyes closure is associated with a substantial amplitude increase of brain activity at ~10Hz with a characteristic occipito-parietal topography. It is probably the strongest signal that can be recorded from the healthy human brain. Because of this non-ambiguity in terms of frequency and spatial topography we will use it here to address the question whether brain areas (i.e. voxels) associated with 10Hz amplitude fluctuations are also characterized by changes in connectivity to some other brain areas/voxels.
Towards this end we have to identify/define the nodal structure of the network where in this case each voxel would be interpreted as a “node”. Furthermore, we have to identify/define the links or “edges” connecting all of the nodes within the network.
Procedure
The data analyses in the context of networks follows the following steps:
- Read the data into MATLAB using ft_definetrial and ft_preprocessing.
- Compute sensor level power spectra and determine peak frequency using ft_freqanalysis and ft_multiplotER.
- Construct a forward model and lead field matrix using ft_volumesegment, ft_prepare_headmodel and ft_prepare_sourcemodel.
- Compute a spatial filter and estimate the amplitude of the sources using ft_sourceanalysis.
- Visualize the results, by first interpolating the sources to the anatomical MRI using ft_sourceinterpolate and plotting this with ft_sourceplot.
- Compute “all-to-all” phase relationship between voxels using ft_connectivityanalysis.
- Compute “node degree” using ft_networkanalysis.
- Visualize the results, again by first interpolating the sources to the anatomical MRI using ft_sourceinterpolate and plotting this with ft_sourceplot.
Preprocessing
Reading the data
The aim is to identify the frequency and topography of an 10Hz oscillation. We first use ft_definetrial and ft_preprocessing to read the continuous data and segment it into epochs of 2 seconds length.
The ft_definetrial and ft_preprocessing functions require the original MEG dataset, which is available from https://download.fieldtriptoolbox.org/tutorial/SubjectRest.zip.
%% read the continuous data and segment into 2 seconds epochs
cfg = [];
cfg.dataset = 'SubjectRest.ds';
cfg.trialdef.triallength = 2;
cfg.trialdef.ntrials = Inf;
cfg = ft_definetrial(cfg);
cfg.continuous = 'yes';
cfg.channel = {'MEG'};
data = ft_preprocessing(cfg);
Artifact rejection
We will first clean the data from potential bad segments such as SQUID jumps and/or bad channels using ft_rejectvisual. Subsequently, we will identify occular and cardiac artifacts by means of ICA using ft_componentanalysis. Since, these type of artifacts are predominately low frequent and we are interested in a 10Hz signal, we will downsample the data using ft_resampledata in order to speed up calculations during ft_componentanalysis and reduce potential working memory issues. Alternatively, you can skip these steps and download the data here.
%% make a visual inspection and reject bad trials/sensors
cfg = [];
cfg.method = 'summary';
cfg.channel = 'MEG';
cfg.layout = 'CTF275.lay';
dataclean = ft_rejectvisual(cfg, data);
% you can check the rejected trial numbers by typing
trlind = [];
for i=1:length(dataclean.cfg.artfctdef.summary.artifact)
trlind(i) = find(data.sampleinfo(:,1)==dataclean.cfg.artfctdef.summary.artifact(i));
end
disp(trlind);
%% downsample the data to speed up component analysis
cfg = [];
cfg.resamplefs = 60;
cfg.detrend = 'yes';
datads = ft_resampledata(cfg, dataclean);
%% use ICA in order to identify cardiac and blink components
cfg = [];
cfg.method = 'runica';
cfg.runica.maxsteps = 50;
cfg.updatesens = 'no';
comp = ft_componentanalysis(cfg, datads);
%% visualize components
% these were the indices of the bad components that were identified
% they may be different if you re-run the ICA decomposition
badcomp = [2 14 18 29];
cfg = [];
cfg.channel = badcomp;
cfg.layout = 'CTF275.lay';
cfg.compscale = 'local';
cfg.continuous = 'yes';
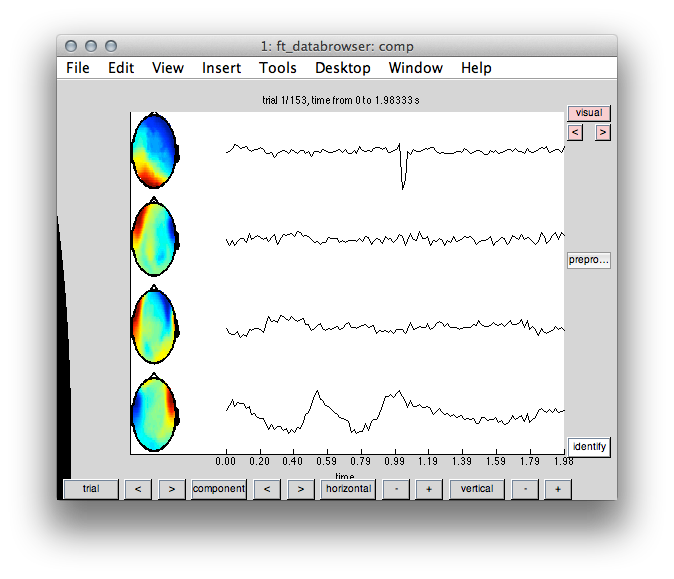
ft_databrowser(cfg, comp);
Figure 1: Topography and time course of IC’s likely reflecting cardiac and eye movement artifacts
We project the component data back to the channel representation, leaving out the bad components.
cfg = [];
cfg.component = [2 14 18 29];
cfg.updatesens = 'no';
dataica = ft_rejectcomponent(cfg, comp);
Spectral analysis
We will analyze the spectral content of the data using ft_freqanalysis and subsequently interactively explore the data with ft_topoplotER and ft_singleplotER. For those interested in more detailed overview of the configuration options and strategies please refer to our video lectures here and also here.
%% compute the power spectrum
cfg = [];
cfg.output = 'pow';
cfg.method = 'mtmfft';
cfg.taper = 'dpss';
cfg.foilim = [1 20];
cfg.tapsmofrq = 2;
cfg.keeptrials = 'no';
fft_data = ft_freqanalysis(cfg, dataica);
%% compute the planar transformation
cfgneigh = [];
cfgneigh.feedback = 'no';
cfgneigh.method = 'template';
cfg = [];
cfg.neighbours = ft_prepare_neighbours(cfgneigh, dataica);
cfg.planarmethod = 'sincos';
planar = ft_megplanar(cfg, dataica);
cfg = [];
cfg.output = 'pow';
cfg.method = 'mtmfft';
cfg.taper = 'dpss';
cfg.foilim = [1 20];
cfg.tapsmofrq = 2;
cfg.keeptrials = 'no';
fft_data_planar = ft_freqanalysis(cfg, planar);
%% plot the topography and the spectrum
figure;
cfg = [];
cfg.layout = 'CTF275.lay';
cfg.xlim = [9 11];
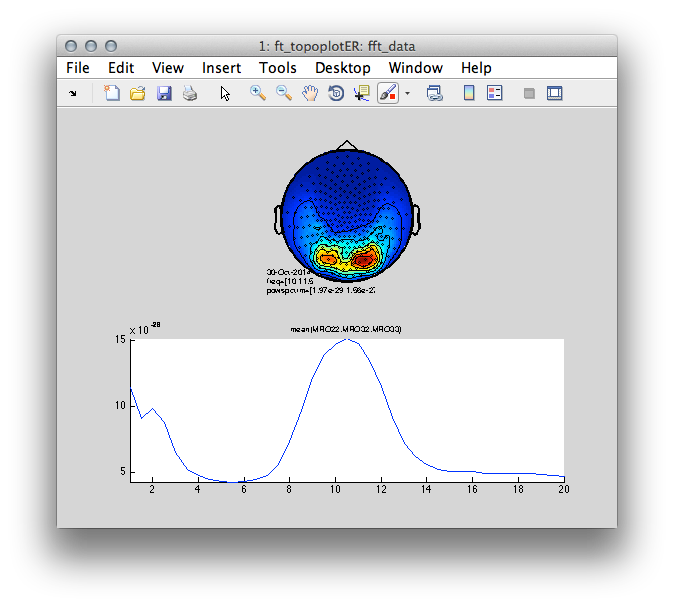
subplot(2,1,1); ft_topoplotER(cfg, fft_data);
cfg = [];
cfg.channel = {'MRO22', 'MRO32', 'MRO33'};
subplot(2,1,2); ft_singleplotER(cfg, fft_data);
Figure 2: Top- scalp topography of oscillatory power centered at 10 Hz. Bottom- power spectrum averaged over three occipital sensors illustrating a clear ~10 Hz peak.
Source analysis
In the following section we will compute the ingredients for accurate reconstruction of the underlying sources. First computing the source model with ft_prepare_sourcemodel. We will use the individual MRI and a mni template source model, which can be downloaded here. If you are not familiar with this strategy, please have a look here.
%% load the required geometrical information
% load the template source model, which is in MNI coordinates
template = load('standard_sourcemodel3d2cm.mat');
load mri % individual mri
load hdm % individual volume model
%% compute the source model
cfg = [];
cfg.warpmni = 'yes';
cfg.template = template.sourcemodel;
cfg.nonlinear = 'yes'; % use non-linear normalization
cfg.mri = mri;
sourcemodel = ft_prepare_sourcemodel(cfg);
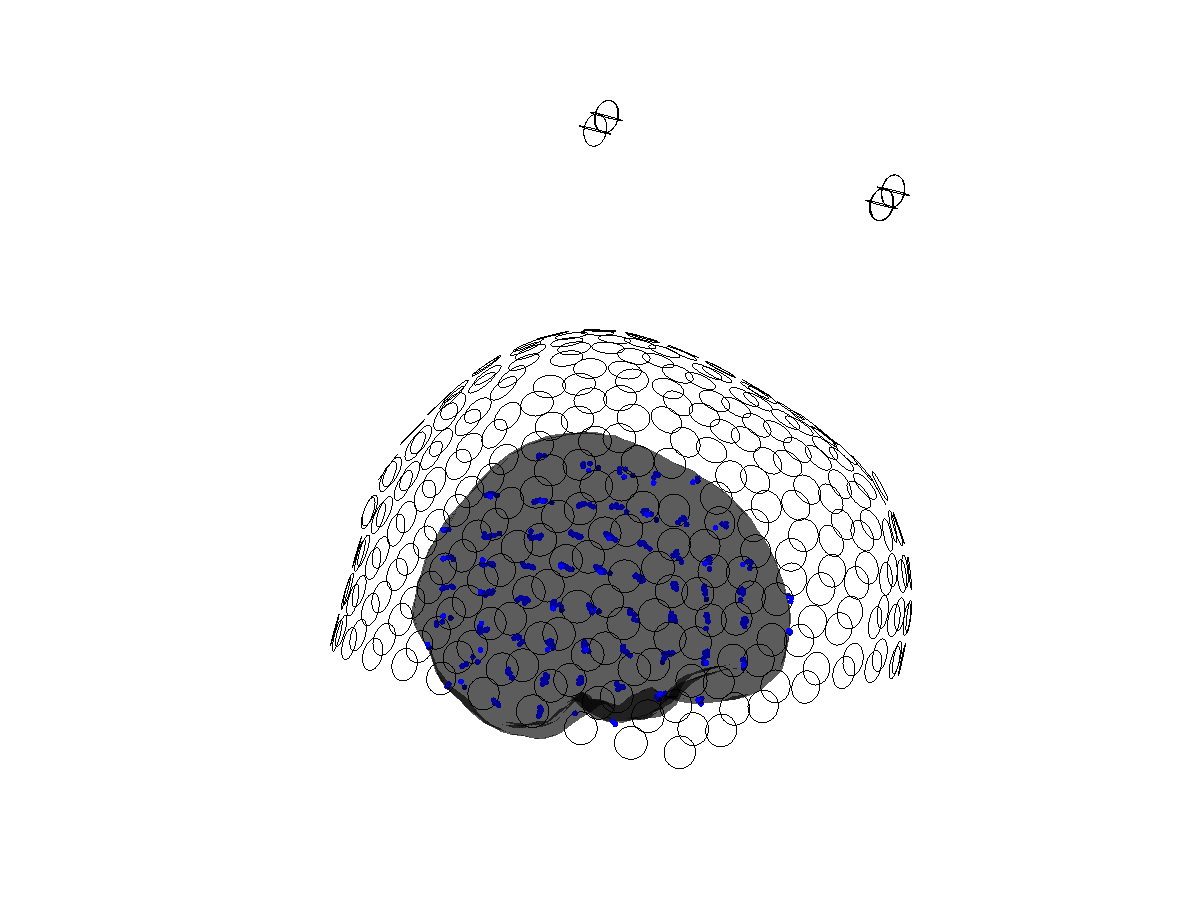
%% check for the correct alignment of sensors (green) headmodel(transparent) and sourcemodel(blue)
figure
% make the headmodel surface transparent
ft_plot_headmodel(hdm, 'edgecolor', 'none');
alpha 0.4
% add the source model positions and sensors
ft_plot_mesh(sourcemodel.pos(sourcemodel.inside,:),'vertexcolor','b');
ft_plot_sens(dataclean.grad);
view([0 -90 0])
Figure 3: Sensors (green), head model (grey) and source model(blue) are properly aligned all in units of cm.
The source model describes a regular 3D grid. Not all positions of the source model are inside the brain. This is represented in the “inside” field.
%% compute sensor level Fourier spectra
cfg = [];
cfg.method = 'mtmfft';
cfg.output = 'fourier';
cfg.keeptrials = 'yes';
cfg.tapsmofrq = 2;
cfg.foi = 10;
freq = ft_freqanalysis(cfg, dataica);
%% compute the leadfield
cfg = [];
cfg.grid = sourcemodel;
cfg.headmodel = hdm;
cfg.channel = {'MEG'};
cfg.grad = freq.grad;
lf = ft_prepare_leadfield(cfg, freq);
%% compute the actual source reconstruction
cfg = [];
cfg.frequency = freq.freq;
cfg.grad = freq.grad;
cfg.method = 'pcc';
cfg.grid = lf;
cfg.headmodel = hdm;
cfg.keeptrials = 'yes';
cfg.pcc.lambda = '5%';
cfg.pcc.projectnoise = 'yes';
source = ft_sourceanalysis(cfg, freq);
%% reduce the source reconstructed data to the dominant orientation
cfg = [];
cfg.projectmom = 'yes';
source_proj = ft_sourcedescriptives(cfg,source);
% and provide the dimension and grid positions of the MRI template positions again
source_proj.dim = template.sourcemodel.dim;
source_proj.pos = template.sourcemodel.pos;
[ftver, ftdir] = ft_version;
if isunix
templatefile = [ftdir '/template/anatomy/single_subj_T1.nii'];
elseif ispc
templatefile = [ftdir '\template\anatomy\single_subj_T1.nii'];
end
template_mri = ft_read_mri(templatefile);
cfg = [];
cfg.parameter = 'nai';
cfg.interpmethod = 'nearest';
source_int = ft_sourceinterpolate(cfg, source_proj, template_mri);
%% plot the neural activity index (power/noise)
cfg = [];
cfg.method = 'ortho';
cfg.funparameter = 'nai';
cfg.maskparameter = cfg.funparameter;
cfg.funcolorlim = [0.0 10];
cfg.opacitylim = [3 10];
cfg.opacitymap = 'rampup';
cfg.funcolormap = 'jet';
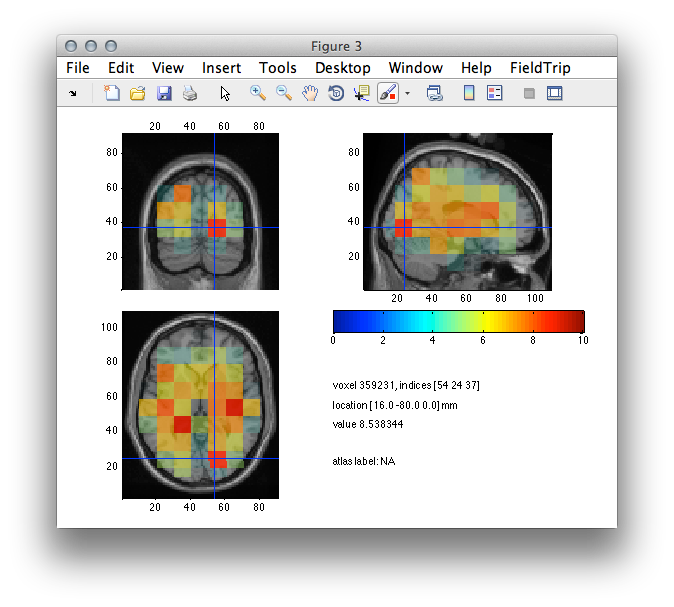
ft_sourceplot(cfg, source_int);
Figure 4: Reconstructed activity (neural activity index) with peak maxima in occipital but also sensorimotor and some deep brain areas.
The accurate judgment of the source reconstructed data is often not straight forward. However, you can make your judgment dependent on the comparison of sensor and source topography. In the present case the activation of the visual areas provide a good match to the observed scalp topography.
cfg = [];
cfg.method = 'ortho';
cfg.funparameter = 'nai';
cfg.location = [16 -80 -2];
cfg.maskparameter = cfg.funparameter;
cfg.funcolorlim = [0.0 10];
cfg.opacitylim = [3 10];
cfg.opacitymap = 'rampup';
cfg.funcolormap = 'jet';
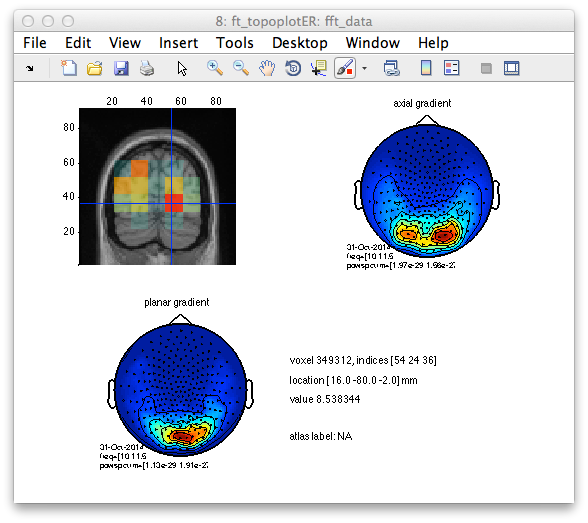
ft_sourceplot(cfg,source_int);
%% add the scalp topographies to the figure
cfg = [];
cfg.layout = 'CTF275.lay';
cfg.xlim = [9.777650 11.309908];
subplot(2,2,2); ft_topoplotER(cfg,fft_data);
title('axial gradient')
cfg = [];
fft_data_planar_cmb = ft_combineplanar(cfg, fft_data_planar);
cfg = [];
cfg.layout = 'CTF275.lay';
cfg.xlim = [9.777650 11.309908];
subplot(2,2,3); ft_topoplotER(cfg, fft_data_planar_cmb);
title('planar gradient')
Figure 5: Reconstructed activity (neural activity index) with peak maxima in occipital areas (top left) together with scalp topographic representation of the signal on the axial (top right) and planar (bottom left) gradients. Note that the presumably bilateral origin suggested by the scalp topography of the axial gradiometers is actually reflecting the in and out going fields of a summed dipolar activity located somewhere in between.
Comparing source reconstruction results to scalp topography is more or less mandatory. However, a potential mismatch shouldn’t prevent you to try out a different strategy. In the beamforming tutorial here the reconstructed activity is represented as a ratio change from pre stimulus baseline. Although there isn’t a baseline we can compare with here, still there is an alternative approach. In the next section we will compute the sensor level alpha power but keep the individual trials. Next we will determine the sensor with a maximum power and use a median split on the trials at that sensor. This would allow us to split the data into trials dominated by high and low alpha power respectively.
%% compute the power spectrum again but keep the individual trials
cfg = [];
cfg.output = 'pow';
cfg.method = 'mtmfft';
cfg.taper = 'dpss';
cfg.foilim = [8 12];
cfg.tapsmofrq = 2;
cfg.keeptrials = 'yes';
fft_data = ft_freqanalysis(cfg, dataica);
%% identify the indices of trials with high and low alpha power
tmp = mean(fft_data.powspctrm,3); % mean over frequencies between 8-12Hz
ind = find(mean(tmp,1)==max(mean(tmp,1))); % find the sensor where power is max
indlow = find(tmp(:,ind)<=median(tmp(:,ind)));
indhigh = find(tmp(:,ind)>=median(tmp(:,ind)));
Next, we will compute the power spectra as above but this time computing them on the planar rather then on the axial gradiometers. Detailed information can be found here and also here.
%% compute the planar gradient
load ctf275_neighb; % this loads a variable 'neighbours', to be used below
dataicatmp = dataica;
dataicatmp.grad = data.grad; % it takes too much time to explain here, why
% this is needed, but otherwise the planar gradient transformation fails
cfg = [];
cfg.neighbours = neighbours;
cfg.planarmethod = 'sincos';
planar = ft_megplanar(cfg, dataicatmp);
clear dataicatmp;
%% compute the power spectrum
cfg = [];
cfg.output = 'pow';
cfg.method = 'mtmfft';
cfg.taper = 'dpss';
cfg.foilim = [1 20];
cfg.tapsmofrq = 2;
cfg.keeptrials = 'no';
cfg.trials = indlow;
tmp = ft_freqanalysis(cfg, planar);
fft_data_planar_low = ft_combineplanar([], tmp);
cfg.trials = indhigh;
tmp = ft_freqanalysis(cfg, planar);
fft_data_planar_high = ft_combineplanar([], tmp);
%% and also do the axial representation for comparison purposes
cfg = [];
cfg.output = 'pow';
cfg.method = 'mtmfft';
cfg.taper = 'dpss';
cfg.foilim = [1 20];
cfg.tapsmofrq = 2;
cfg.keeptrials = 'no';
cfg.trials = indlow;
fft_data_low = ft_freqanalysis(cfg,dataica);
cfg.trials = indhigh;
fft_data_high = ft_freqanalysis(cfg,dataica);
Subsequently, we will compute the difference between high and low alpha conditions using ft_math for both axial and planar representation and plot the corresponding scalp topographies along with the power spectra.
%% compute the difference between high and low
cfg = [];
cfg.parameter = 'powspctrm';
cfg.operation = 'subtract';
diff = ft_math(cfg, fft_data_high, fft_data_low);
diff_planar = ft_math(cfg, fft_data_planar_high, fft_data_planar_low);
diff_axial = ft_math(cfg, fft_data_high, fft_data_low);
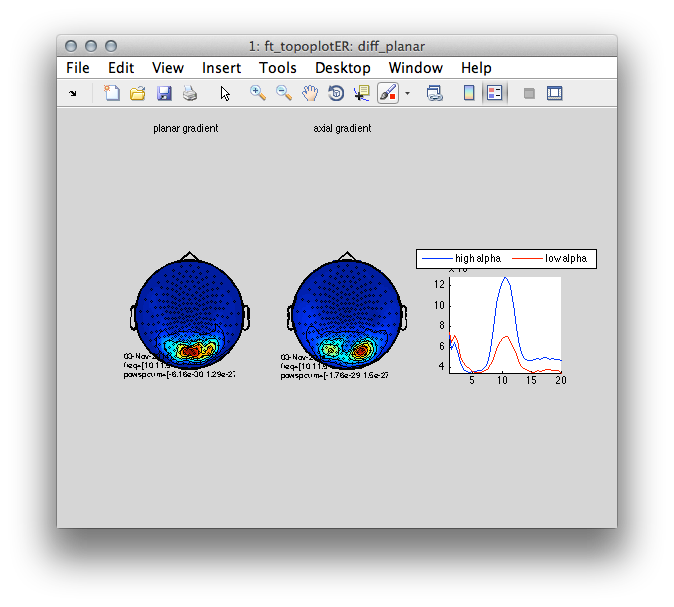
%% plot the topography of the difference along with the spectra
figure;
cfg = [];
cfg.layout = 'CTF275.lay';
cfg.xlim = [9.777650 11.309908];
subplot(1,3,1); ft_topoplotER(cfg, diff_planar); title ('planar gradient')
subplot(1,3,2); ft_topoplotER(cfg, diff_axial); title ('axial gradient')
cfg = [];
cfg.channel = {'MLO21', 'MRO31'};
subplot(1,3,3); ft_singleplotER(cfg,fft_data_high, fft_data_low);
obj = subplot(1,3,3);
set(obj, 'Position', [.7 .37 .2 .3])
title('')
legend('high alpha','low alpha','Location','northoutside','Orientation','horizontal');
Figure 6: Planar (left) and axial (middle) topography of the 10 Hz difference between the high and the low alpha conditions. Right- power spectra split by condition high (blue) and low alpha (red).
Now we will compute the source analysis steps again as illustrated above, however we will use a common filter approach in order to avoid a filter estimated bias being responsible for potential condition differences, see also here and here for further information on common filters.
%% compute fourier spectra for frequency of interest
cfg = [];
cfg.method = 'mtmfft';
cfg.output = 'fourier';
cfg.keeptrials = 'yes';
cfg.tapsmofrq = 2;
cfg.foi = 10;
cfg.trials = indlow;
freq_low = ft_freqanalysis(cfg, dataica);
cfg.trials = indhigh;
freq_high = ft_freqanalysis(cfg, dataica);
%% compute the beamformer filters based on the entire data
cfg = [];
cfg.frequency = freq.freq;
cfg.grad = freq.grad;
cfg.method = 'pcc';
cfg.grid = lf;
cfg.headmodel = hdm;
cfg.keeptrials = 'yes';
cfg.pcc.lambda = '5%';
cfg.pcc.projectnoise = 'yes';
cfg.pcc.keepfilter = 'yes';
source = ft_sourceanalysis(cfg, freq);
% use the precomputed filters
cfg = [];
cfg.frequency = freq.freq;
cfg.grad = freq.grad;
cfg.method = 'pcc';
cfg.grid = lf;
cfg.sourcemodel.filter = source.avg.filter;
cfg.headmodel = hdm;
cfg.keeptrials = 'yes';
cfg.pcc.lambda = '5%';
cfg.pcc.projectnoise = 'yes';
source_low = ft_sourceanalysis(cfg, freq_low);
source_high = ft_sourceanalysis(cfg, freq_high);
%% project dipole moments along the dominant orientation
cfg = [];
cfg.projectmom = 'yes';
source_proj_high = ft_sourcedescriptives(cfg,source_high);
source_proj_low = ft_sourcedescriptives(cfg,source_low);
source_proj_high.dim = template.sourcemodel.dim;
source_proj_high.pos = template.sourcemodel.pos;
source_proj_low.dim = template.sourcemodel.dim;
source_proj_low.pos = template.sourcemodel.pos;
%% interpolate the results onto an anatomical brain template
[ftver, ftdir] = ft_version;
if isunix
templatefile = [ftdir '/template/anatomy/single_subj_T1.nii'];
elseif ispc
templatefile = [ftdir '\template\anatomy\single_subj_T1.nii'];
end
template_mri = ft_read_mri(templatefile);
cfg = [];
cfg.parameter = 'pow';
cfg.interpmethod = 'nearest';
source_int_high = ft_sourceinterpolate(cfg, source_proj_high, template_mri);
source_int_low = ft_sourceinterpolate(cfg, source_proj_low, template_mri);
Now instead of computing the neural activity index by contrsting against the noise, we will compute the power change in condition high relative to that of low.
cfg = [];
cfg.operation = '(x1-x2)/x2';
cfg.parameter = 'pow';
source_int = ft_math(cfg, source_int_high, source_int_low)
We create a mask that plots a fraction, i.e. most active brain areas.
% up to 50 percent of maximum
source_int.mask = source_int.pow > max(source_int.pow(:))*.5;
% copy the anatomy
source_int.anatomy = source_int_high.anatomy;
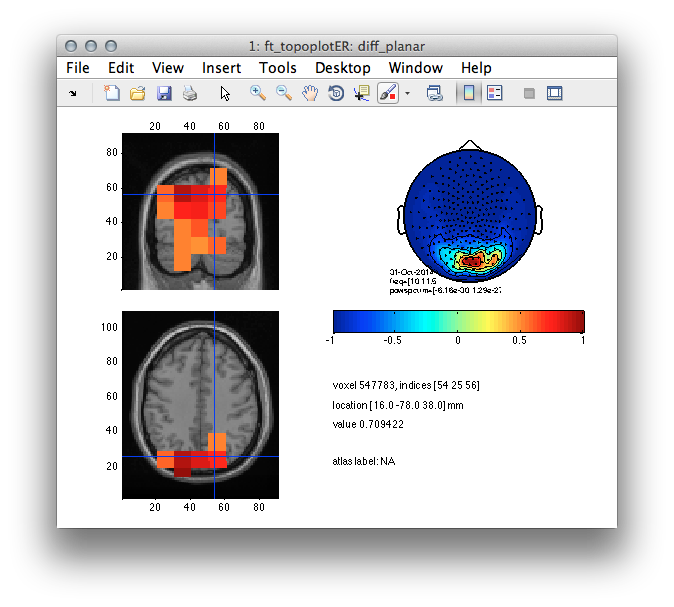
Now we plot the result together with the scalp topography again.
cfg = [];
cfg.method = 'ortho';
cfg.funparameter = 'pow';
cfg.maskparameter = 'mask';
cfg.funcolorlim = [-1 1];
cfg.location = [16 -78 38];
cfg.funcolormap = 'jet';
ft_sourceplot(cfg, source_int);
cfg = [];
cfg.layout = 'CTF275.lay';
cfg.xlim = [9.777650 11.309908];
subplot(2,2,2); ft_topoplotER(cfg, diff_planar);
Figure 7: Source reconstructed activity illustrating the relative change in alpha power increase between the high and low alpha conditions.
Now comparing the results from Figure 4 and Figure 7 yields two important observations. Namely, both approaches are capable of reconstructing occipital neural activity. Yet, due to an SNR trade-off in the second case the reconstructed results are less ambiguous. That is, the alpha power increase during eyes closed happens predominantly in occipito-parietal brain regions. There is little room for speculations about the involvement of sensorimotor and deep brain areas.
Network analysis
Finally we will represent the communication between voxels in terms of a “network”. That is, each dipole location will reflect a network “node” and all pairwise connections or “edges” will be quantified with the coherence coefficient. This results in a 720x720 matrix (in this case). However we are interested in the communication between all voxel that are defined as ‘inside’ or within the skull and we don’t care about the ‘outside’ ones. Often the brain volume is discretized in much more smaller voxel size resulting in much more bigger matrices that need to be dealth with in memory.
We will first reduce the size of the matrix by calling ft_source2sparse. Subsequently, we will call ft_connectivityanalysis with the configuration options cfg.method = ‘coh’; and cfg.complex = ‘absimag’;. This syntax will return only the imaginary part of the coherence spectrum and effectivly suppress spurious coherence driven by volumeconduction (Nolte et al. Identifying true brain interaction from EEG data using the imaginary part of coherence. Clinical Neurophysiology, 2004; 115; 2292-2307).
After computing this memory demanding step we will return to the full representation of the data by calling ft_source2full.
Next, we will use ft_networkanalysis with the configuration options cfg.method = ‘degrees’; and cfg.threshold = .1;. The former one refers to one of the most fundamental metrics in graph theory- node degree (Ed Bullmore and Olaf Sporns: Complex brain networks: graph theoretical analysis of structural and functional systems. 2009 Nat Rev Neurosci, vol 10(3) pp. 186-198). Node degree refers to the number of links connected to the node and can be directed or undirected (as in this tutorial). Prerequisite for calculating node degree is the computation of the so called adjacency matrix (AM). This is a binary matrix of the same size as our coherence spectrum matrix (720 x 720) with 1 and 0 for link or no link between pairs respectively. Hence the coherence spectrum has to be thresholded at some value where everything below will be 0 and everything above will be replaced by 1. This is provided by the configuration option cfg.threshold and it is one of the most critical step in graph-theoretical networkanalysis of M/EEG data. There are several ways to determine the threshold, for instance based on some statistical parameterization or previous observation in the literature, yet all of them are and remain arbitrary. Here we used an arbitrary value of 0.1.
%% reduce memory demands and compute connectivity
% compute the sparse representation
source_sparse = ft_source2sparse(source_proj);
% then compute connectivity
cfg=[];
cfg.method ='coh';
cfg.complex = 'absimag';
source_conn = ft_connectivityanalysis(cfg, source_sparse);
%% reassign the connectivity
cohspctrm_full = nan(size(source_proj.pos,1));
for i=1:size(source_conn.pos)
pos1 = source_conn.pos(i,1:3);
pos2 = source_conn.pos(i,4:6);
ind1 = find(source_proj.pos(:,1)==pos1(1) & source_proj.pos(:,2)==pos1(2) & source_proj.pos(:,3)==pos1(3));
ind2 = find(source_proj.pos(:,1)==pos2(1) & source_proj.pos(:,2)==pos2(2) & source_proj.pos(:,3)==pos2(3));
cohspctrm_full(ind1,ind2) = source_conn.cohspctrm(i);
end
% then go to the 'full' representation again
source_conn_full = []
source_conn_full.pos = source_proj.pos;
source_conn_full.dim = source_proj.dim;
source_conn_full.inside = source_proj.inside;
source_conn_full.cohspctrm = cohspctrm_full;
source_conn_full.dimord = 'pos_pos';
%% compute graph metric
cfg = [];
cfg.method = 'degrees';
cfg.parameter = 'cohspctrm';
cfg.threshold = .1;
network = ft_networkanalysis(cfg,source_conn_full);
%% interpolate on anatomical mri and plot the result
network.pos = template.sourcemodel.pos;
network.dim = template.sourcemodel.dim;
network.inside = template.sourcemodel.inside;
cfg = [];
cfg.parameter = 'degrees';
cfg.interpmethod = 'nearest';
network_int = ft_sourceinterpolate(cfg, network, template_mri);
%%
cfg = [];
cfg.method = 'ortho';
cfg.funparameter = 'avg.degrees';
cfg.funcolormap = 'jet';
cfg.location = 'max';
cfg.funparameter = 'degrees';
ft_sourceplot(cfg, network_int);
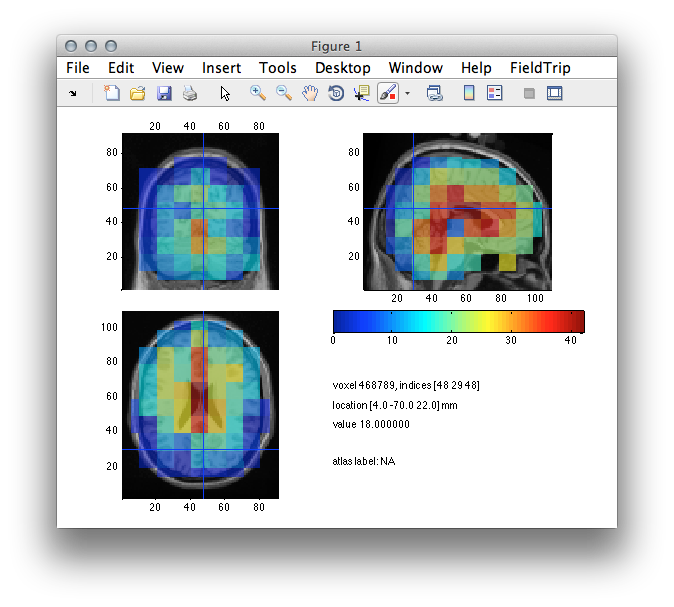
Figure 8: Color coded node degree distribution based on imaginary part of coherency. Cold colors indicated little or disconnected nodes, warm colors indicate highly connected/integrated nodes.
Figure 8 pictures the node degree distribution across the entire brain volume. But what does a node degree of 30 mean? And why 30? The degree of a given node quantifies the number of connections that link to that node. In our case we the dark red nodes in the occipital cortex express a node degree of around 30, which means that they link to approximately 30 other nodes withing the network. Yet, 30 is defined by the threshold we choose in the configuration settings during the call to ft_networkanalysis. The maximum value of the node degree is limited by the total number of network nodes which in our case is *numel(sourcemodel.inside)= 372*. It is up to you to decide on the value of the thresholding parameter, which is often not trivial and hard to justify. Therefore it is one of the critical steps in graph theoretical connectivity analyis.
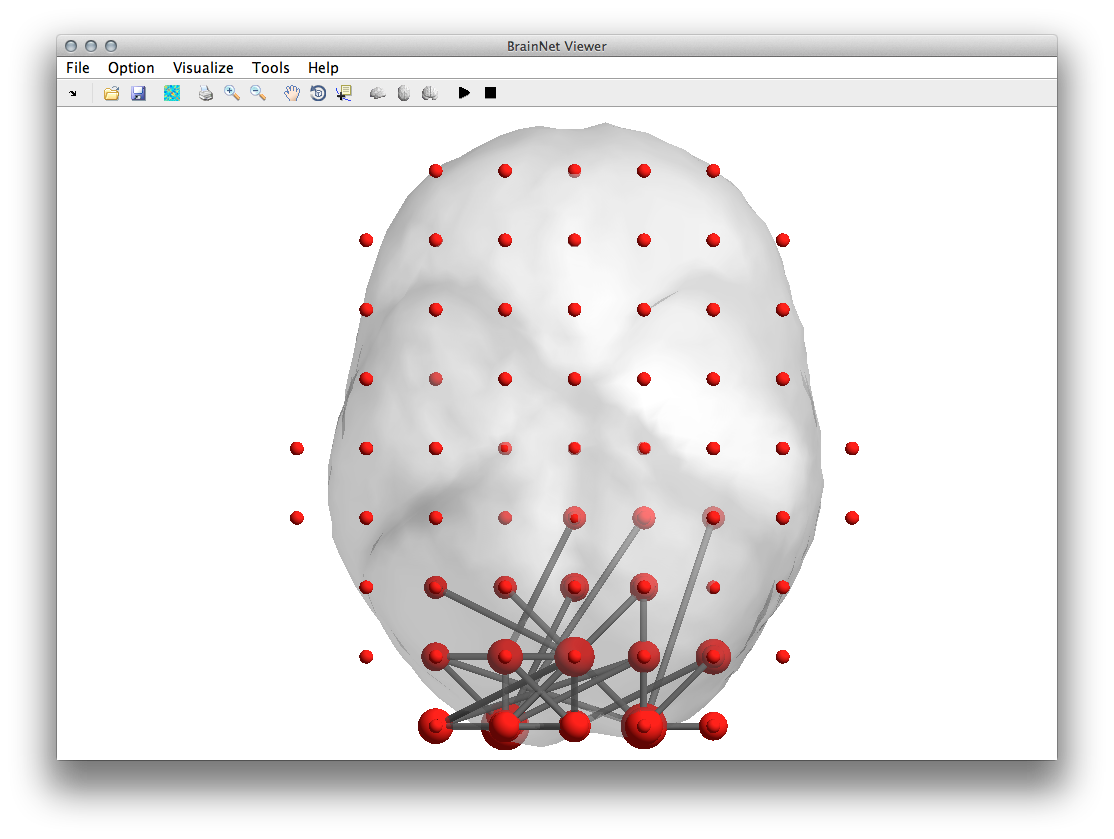
It is also possible to plot the nodal size along with the respective edge pattern. For this we will use the BrainNet Viewer toolbox (Xia M, Wang J, He Y (2013) BrainNet Viewer: A Network Visualization Tool for Human Brain Connectomics. Plos ONE 8: e68910) that can be downloaded here. After you set the BrainNet Viewer toolbox on your MATLAB path you need to generate two files that represented the nodal structure of the data node.node and the corresponding edges edge.edge.
% we increase the threshold here to highlight the dominant links
edge = source_conn.cohspctrm >.15;
dlmwrite('edge.edge',edge,'\t');
load standard_sourcemodel3d2cm.mat
node = zeros(372,6)
node(:,1:3) = sourcemodel.pos(sourcemodel.inside,:)
node(:,4) = 4;
node(:,5) = network.degrees(network.inside);
node(:,6) = 0;
node(:,1:3) = node(:,1:3)*10
dlmwrite('node.node',node,' ');
You can download the volume model mesh.nv of the standard mni brain here. Alternatively you can use the templates provided with the BrainNet Viewer toolbox. Please refer to the corresponding manual here.Now you are ready to to plot the graph by typing
BrainNet_MapCfg('/yourpath/mesh.nv','/yourpath/node.node','/yourpath/edge.edge');
view([0 -90 0])
Of course one can use also phase locking value or some other metric for quantification of communication between the nodes. Here we will compute the same lines of code again where the only difference is in the specification of the connectivity method. In order to plot the result the above lines of code can be used again.
cfg = [];
cfg.method = 'plv';
source_conn = ft_connectivityanalysis(cfg, source_sparse);
%% then compute graph metric
source_conn.dim = source_sparse.dim;
source_conn.outside = source_proj.outside;
% then go to the 'full' representation again
source_conn_full = ft_source2full(source_conn);
source_conn_full.dimord='pos_pos';
%%
fn=fieldnames(source_conn_full);
cfg = [];
cfg.method = 'degrees';
cfg.parameter = fn{4};
cfg.threshold = .5;
deg = ft_networkanalysis(cfg,source_conn_full);
Exercise 1
Compare both network configurations. Obiviously, they have little in common.
Why? Discuss the difference between ‘icoh’ and ‘plv’.
What is the role of the spatial filter?