Sensor-level ERF, TFR and connectivity analyses
Introduction
In this tutorial, we will provide an overview of several sensor-level analyses to help you get started working with FieldTrip. We will work on a dataset (Schoffelen, Poort, Oostenveld, & Fries (2011) Selective Movement Preparation Is Subserved by Selective Increases in Corticomuscular Gamma-Band Coherence. J Neurosci. 31(18):6750-6758) collected during an experiment where subjects were instructed to fixate on a screen. Each trial started with the presentation of a cue pointing either rightward or leftward. This cue indicated which hand the subject had to use for the trial’s response. Next, the subjects were instructed to extend both their wrists. After a baseline interval of 1s, an inward drifting grating was visually presented. Then, after an unpredictable delay, the stimulus changed speed, after which the subjects had to increase their wrist extension on the one cued side only. This experimental design is illustrated in Figure 1. Magneto-encephalography (MEG) data was collected using a 151-channel CTF system. Also, electromyography (EMG) data was collected from electrodes attached to the bilateral musculus extensor carpi radialis longus.
Figure 1: illustration of the experimental paradigm.
We will perform three types of analyses in this tutorial. We will start by looking at the event-related field (ERF) surrounding visual stimulus onset. Next, we will examine the induced oscillatory activity during the visual stimulation. Finally, we will investigate the connectivity between the cortex and the muscle, by computing MEG-EMG coherence.
This tutorial does not cover the steps required to import data into FieldTrip and preprocess it. This is covered in the preprocessing tutorial, which is recommended reading material before starting the present tutorial. This tutorial also does not cover the details of the various options available for doing spectral analysis. Please refer to the time-frequency analysis tutorial for that.
Reading in the data
For your convenience, the data has already been preprocessed. You can download subjectK.mat and load it in memory data with:
load subjectK
This will give you two data structures in your workspace: data_left, containing the trials where the subjects had to respond with the left wrist, and data_right, where the right wrist was cued.
Take a look at one of the data structure
data_left =
hdr: [1x1 struct]
label: {153x1 cell}
time: {1x140 cell}
trial: {1x140 cell}
fsample: 400
grad: [1x1 struct]
cfg: [1x1 struct]
sampleinfo: [140x2 double]
Most important for now are the trial, time, and label fields. The trial field contains the data for each trial as channel X time points matrices. The time field contains the time axis for each trial, and the label field contains the names of the channels in the data.
Plot the data for the first trial, 130th channe
plot(data_left.time{1}, data_left.trial{1}(130,:));
Which channel is the 130th channel?
Time point 0 in all trials corresponds to the onset of the visual stimulation. Trials end when the visual stimulus changed its speed, which is when the subject had to move their wrist (so the data for the actual movement is not in the trials). The visual stimulus speed change happened at an unpredictable time after t=0, so not all trials are the same length. To see this, plot some trials like this:
for k = 1:10
plot(data_left.time{k}, data_left.trial{k}(130,:)+k*1.5e-12);
hold on;
end
plot([0 0], [0 1], 'k');
ylim([0 11*1.5e-12]);
set(gca, 'ytick', (1:10).*1.5e-12);
set(gca, 'yticklabel', 1:10);
ylabel('trial number');
xlabel('time (s)');
Figure 1a: Some example trials, with time t=0 marked.
Event-related analysis
When analyzing EEG or MEG signals, the aim is to investigate the modulation of the measured brain signals with respect to a certain event. However, due to intrinsic and extrinsic noise in the signals - which in single trials is often higher than the signal evoked by the brain - it is typically required to average data from several trials to increase the signal-to-noise ratio(SNR). One approach is to repeat a given event in your experiment and average the corresponding EEG/MEG signals. The assumption is that the noise is independent of the events and thus reduced when averaging, while the effect of interest is time-locked to the event. The approach results in ERPs and ERFs for respectively EEG and MEG. Timelock analysis can be used to calculate ERPs/ERFs.
In FieldTrip, ERPs and ERFs are calculated by ft_timelockanalysis. For this particular dataset, we are interested in the ERF locked to visual stimulation. Since visual stimulation was the same in both the response-right and response-left conditions, we can combine the two data sets using ft_appenddata:
cfg = [];
data = ft_appenddata(cfg, data_left, data_right);
Next, proceed to compute the ER
cfg = [];
cfg.channel = 'MEG';
tl = ft_timelockanalysis(cfg, data);
Plotting the results
FieldTrip provides several options for visualizing the results of event-related analyses: ft_singleplotER, ft_multiplotER, and ft_topoplotER (see the plotting tutorial for an extensive introduction to your plotting options). In most cases, ft_multiplotER is the most convenient start, as it provides easy access to the other two visualization methods through the graphical user interface. Call it like this:
cfg = [];
cfg.showlabels = 'yes';
cfg.showoutline = 'yes';
cfg.layout = 'CTF151_helmet.mat';
ft_multiplotER(cfg, tl);
Note that we request channel labels and head outline showing, and with a particular template layout corresponding to our MEG acquisition system. The output should look like this:
Figure 2: event-related field for each MEG sensor.
As you can see, the event-related field for each MEG sensor is displayed at a location corresponding to the approximate location of each sensor.
The nice thing about this multiplot is that it is interactive: it is possible to select sensors and view an average plot (corresponding to an ft_singleplotER) of those sensors. There seems to be an interesting deflection in the ERF around the left occipitoparietal sensors. Go ahead and select those, and click the selection box that comes up.
Figure 3: click the box to show the average of the selected sensors.
The plot that comes up shows a major deflection around 300m
Figure 4: average ERF for some left posterior sensors.
Again, you can select a time range and click it to bring up a topographical plot (ft_topoplotER) of the ERF averaged over the selected time window. Select the peak around 300ms and click i
Figure 5: topographical representation of the ERF deflection around 300ms after visual stimulus onset.
Given that the CTF system uses axial gradiometers (i.e. detecting the magnetic gradient orthogonal to the scalp), what electrical dipole configuration would explain the observed field pattern in the above figure?
Feel free to click around a bit in the multi- and singleplots to explore the characteristics of the ERF.
Use the cfg.baseline option in ft_multplotER to correct the ERF for the baseline in the pre-stimulus interval.
The planar gradient
The CTF MEG system has (151 in this dataset, or 275 in newer systems) first-order axial gradiometer sensors that measure the gradient of the magnetic field in the radial direction, i.e. orthogonal to the scalp. Often it is helpful to interpret the MEG fields after transforming the data to a planar gradient configuration, i.e. by computing the gradient tangential to the scalp. This representation of MEG data is comparable to the field measured by planar gradiometer sensors. One advantage of the planar gradient transformation is that the signal amplitude typically is largest directly above a source, whereas with axial gradient the signal amplitude is largest away from the source.
We can compute the planar magnetic gradient using ft_megplanar, which gives us the planar gradient in the vertical and horizontal orientations. For visualization, and many subsequent analysis steps, these components need to be combined, which is implemented by ft_combineplanar. Since averaging is a linear operation, it does not matter if we convert the data to planar gradient before or after the call to ft_timelockanalysis. However, later on we will do frequency analysis, where the order does matter, so we will use the same order here. To compute the planar gradient and recompute the ERFs on this dat
cfg = [];
cfg.method = 'template';
cfg.template = 'CTF151_neighb.mat';
neighbours = ft_prepare_neighbours(cfg, data);
cfg = [];
cfg.method = 'sincos';
cfg.neighbours = neighbours;
data_planar = ft_megplanar(cfg, data);
cfg = [];
cfg.channel = 'MEG';
tl_planar = ft_timelockanalysis(cfg, data_planar);
cfg = [];
tl_plancmb = ft_combineplanar(cfg, tl_planar);
Note that we create a ‘neighbours’ structure before calling ft_megplanar. This is required by ft_megplanar because the ‘sincos’ algorithm needs to know which channels are adjacent to one another. Plot the results again
cfg = [];
cfg.showlabels = 'yes';
cfg.showoutline = 'yes';
cfg.layout = 'CTF151_helmet.mat';
ft_multiplotER(cfg, tl_plancmb);
The order in which you do the combining the planar channels and averaging does matter, since the combining consists of a non-linear transform.
Please be advised that this might result in unexpected and undesirable effects due to different number of trials and/or due to baselining effects. In general we recommend to not use combined planar gradients for ERFs, unless you know what you are doing. See also this example.
Time-frequency analysis
Background
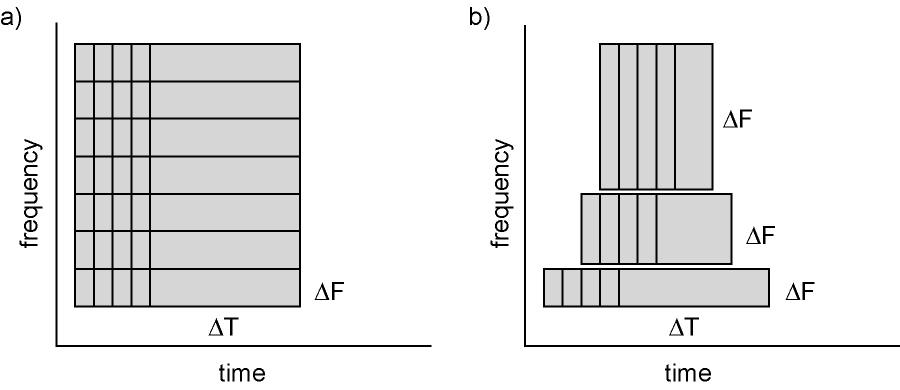
Oscillatory components contained in the ongoing EEG or MEG signal often show power changes relative to experimental events. These signals are not necessarily phase-locked to the event and will not be represented in event-related fields and potentials (Tallon-Baudry and Bertrand (1999)). The goal of this section is to compute and visualize event-related changes by calculating time-frequency representations (TFRs) of power. This will be done using analysis based on Fourier analysis and wavelets. The Fourier analysis will include the application of multitapers (Mitra and Pesaran (1999), Percival and Walden (1993)) which allow a better control of time and frequency smoothing.
Calculating time-frequency representations of power is done using a sliding time window. This can be done according to two principles: either the time window has a fixed length independent of frequency, or the time window decreases in length with increased frequency. For each time window the power is calculated. Prior to calculating the power one or more tapers are multiplied with the data. The aim of the tapers is to reduce spectral leakage and control the frequency smoothing.
Figure 6: Time and frequency smoothing. (a) For a fixed length time window the time and frequency smoothing remains fixed. (b) For time windows that decrease with frequency, the temporal smoothing decreases and the frequency smoothing increases.
If you want to know more about tapers/ window functions you can have a look at this Wikipedia page. Note that Hann window is another name for Hanning window used in this tutorial. There is also a Wikipedia site about multitapers, to take a look at it click here.
Time-frequency representations using Hanning tapers
We will here describe how to calculate time frequency representations using Hanning tapers. When choosing for a fixed window length procedure the frequency resolution is defined according to the length of the time window (delta T). The frequency resolution (delta f in figure 1) = 1/length of time window in sec (delta T in figure 1). Thus a 500 ms time window results in a 2 Hz frequency resolution (1/0.5 sec= 2 Hz) meaning that power can be calculated for 2 Hz, 4 Hz, 6 Hz etc. An integer number of cycles must fit in the time window.
To compute our time-frequency representation (TFR), we will first subselect a piece of our trials using ft_redefinetrial. This is done to increase the speed at which the subsequent analysis will run. We need a part of the baseline interval and a part of the stimulation interval, so we choose the interval from -0.8s to 1.0s
cfg = [];
cfg.toilim = [-0.8 1];
cfg.minlength = 'maxperlen'; % this ensures all resulting trials are equal length
data_small = ft_redefinetrial(cfg, data_planar);
The structure data_small contains less trials than the original data, because we want trials that last until at least 1s after stimulus onset. Recall that not all trials last that long, because the visual stimulus speed change might have happened before t=1s already. Note that we are again using the planar gradient data, in order to make interpreting the results easier. Now we move on to using ft_freqanalysis to compute our TFR using a 0.2s window size:
cfg = [];
cfg.method = 'mtmconvol';
cfg.taper = 'hanning';
cfg.channel = 'MEG';
% set the frequencies of interest
cfg.foi = 20:5:100;
% set the timepoints of interest: from -0.8 to 1.1 in steps of 100ms
cfg.toi = -0.8:0.1:1;
% set the time window for TFR analysis: constant length of 200ms
cfg.t_ftimwin = 0.2 * ones(length(cfg.foi), 1);
% average over trials
cfg.keeptrials = 'no';
% pad trials to integer number of seconds, this speeds up the analysis
% and results in a neatly spaced frequency axis
cfg.pad = 2;
freq = ft_freqanalysis(cfg, data_small);
Again we have to combine the two components of the planar gradient
cfg = [];
freq = ft_combineplanar(cfg, freq);
Plotting
Then we can plot the results using ft_multiplotTFR:
cfg = [];
cfg.interactive = 'yes';
cfg.showoutline = 'yes';
cfg.layout = 'CTF151_helmet.mat';
cfg.baseline = [-0.8 0];
cfg.baselinetype = 'relchange';
cfg.zlim = 'maxabs';
ft_multiplotTFR(cfg, freq);
Note the baseline and baselinetype parameters. These govern what baseline correction is applied to the data before plotting. In this case, we want to plot the relative change of our power data with respect to the interval between -0.8s and 0s (corresponding to the no-stimulation baseline interval in the experimental design).
Figure 7: Time-frequency representation using a Hanning taper with a fixed window length.
This is an interactive plot, so just as with the event-related part you can select sensors and click to get an average TFR. With this, you can select a time and frequency range and plot a topography.
Click around the multiplot to explore the visual gamma response and its topography!
Overview of the conducted analysis
In a next step, you can get an overview of your analyses by clicking on the FieldTrip menu item and selecting “Show pipeline
Exactly the same can be achieved using ft_analysispipeline as follow
cfg = [];
ft_analysispipeline(cfg, freq);
The function ft_analysispipeline puts all conducted analysis steps into perspective and visualizes them in a flowchart
By clicking on one of the boxes (in MATLAB), a new figure will appear that shows all cfg-options that were used to in the respective function.
Cortico-muscular coherence
Up to now, we have exclusively looked at the characteristics of the MEG signal. However, as explained in the introduction, this data set also contains EMG data for the left and right wrist muscles. These signals provide excellent reference signals to investigate the connectivity between the cortex and the muscle. This is what we will now look at; specifically, we will compute the coherence between the MEG signal and the left and right EMG signals.
Coherence is computed in the frequency domain by normalizing the magnitude of the summed cross-spectral density between two signals by their respective power. For each frequency bin the coherence value is a number between 0 and 1. The coherence values reflect the consistency of the phase difference between the two signals at a given frequency.
This experiment was conducted to examine whether connectivity between the cortex and the muscle is altered in reaction to a response cue (recall that subjects were cued to respond either with the left or right hand at the beginning of each trial, but that both hands were lifted). We will now look at corticomuscular coherence irrespective of the response cue, and simply pool the two conditions. The cleanest time window in which to estimate this effect is the baseline window, with no visual stimulation present. Therefore, we subselect the baseline data to subject to our coherence analysi
cfg = [];
cfg.toilim = [-1 -0.0025];
cfg.minlength = 'maxperlen'; % this ensures all resulting trials are equal length
data_stim = ft_redefinetrial(cfg, data);
Coherence is one of the metrics which can be computed by ft_connectivityanalysis. To compute coherence, this function needs the cross-spectral density matrix as input. This can be computed by ft_freqanalysis, the same function we used earlier to compute TFRs. By default ft_freqanalysis only outputs power values, and not the cross-spectral density. To change this, we have to specify cfg.output = ‘powandcsd’. Also, while previously we wanted to get a time-resolved estimate of power, we are now interested in a non-time-resolved quantity, namely coherence. Therefore we use cfg.method = ‘mtmfft’ instead of cfg.method = ‘mtmconvol
cfg = [];
cfg.output = 'powandcsd';
cfg.method = 'mtmfft';
cfg.taper = 'dpss';
cfg.tapsmofrq = 5;
cfg.foilim = [5 100];
cfg.keeptrials = 'yes';
cfg.channel = {'MEG' 'EMGlft' 'EMGrgt'};
cfg.channelcmb = {'MEG' 'EMGlft'; 'MEG' 'EMGrgt'};
freq_csd = ft_freqanalysis(cfg, data_stim);
Note that some other things are different as well. cfg.keeptrials = ‘yes’ because phase estimates are required for each individual trial (i.e., averaging phase over trials is generally not a good idea). We use multitapers (‘dpss’) this time, to have a good control over our spectral smoothing. The desired smoothing is specified in cfg.tapsmofrq (‘taper smoothing frequency’). Finally, note that cfg.channel now also includes the two EMG channels, and that cfg.channelcmb is a 2x2 cell-array specifying that we want to compute the cross-spectral density between the MEG and the left EMG, and the MEG and the right EMG.
After computing the cross-spectral density, we can invoke ft_connectivityanalysis to compute the coherenc
cfg = [];
cfg.method = 'coh';
cfg.channelcmb = {'MEG' 'EMG'};
conn = ft_connectivityanalysis(cfg, freq_csd);
Plotting
Non-time-resolved spectra (such as our coherence spectrum) can be visualized using the same functions as for the plotting of event-related data, in particular ft_multiplotER is of relevance. The plotting functions plot the coherence of one channel X to typically all MEG channels. The channel X is determined by the parameter cfg.refchannel
cfg = [];
cfg.parameter = 'cohspctrm';
cfg.xlim = [5 80];
cfg.refchannel = 'EMGlft';
cfg.layout = 'CTF151_helmet.mat';
cfg.showlabels = 'no';
cfg.interactive = 'yes';
figure;
ft_multiplotER(cfg, conn);
Again, this is an interactive plot, so click around it to get a nice overview of the exact spectrum and the topography of the peak (which is in the beta frequency range).
Figure 8: results of sensor-level analysis of corticomuscular coherence. Reference channel was the left EMG.
After exploring the coherence results when the reference channel is the left EMG, do the same for the right EMG (which is called ‘EMGrgt’). What do you conclude?
Try changing the cfg.tapsmofrq parameter in the ft_freqanalysis step. How does this affect the resulting coherence spectrum?
Summary and suggested further reading
This tutorial gave an overview of some options available in FieldTrip for doing sensor-level analysis. We started by computing an event-related field evoked by visual stimulation and computing a planar gradient representation. Next, time-frequency analysis was performed and revealed induced visual gamma activity. Finally, we discovered increased cortico-muscular coherence in the beta band of wrist muscles with the contralateral hemisphere.
After having finished this tutorial, you might want to read through the tutorial on time-frequency analysis, which provides more details on the various tapers available and their implications. Alternative follow-ups would be the tutorial on beamformers for source reconstruction or, for details on statistics, one of the statistics tutorials.
Furthermore, you can explore relevant example scripts:
and frequently asked questions: