Reconstructing source activity using beamformers

Introduction

In this tutorial you will learn about applying beamformer techniques in the time domain, using MEG data from an Neuromag/Elekta/MEGIN system. Using beamformers on Neuromag/Elekta/MEGIN data is somewhat more challenging than using beamformers on (for instance) CTF data. This is for two reasons: 1) Elekta MEG data consists of signals of different sensor types (magnetometers and planar gradiometers), and 2) the data are often heavily rank-deficient due to the application of the Maxfilter to clean the data of (movement) artifacts.

It is expected that you understand the previous steps of preprocessing and filtering the sensor data, as covered in the raw2erp tutorial. Also, you need to understand how to create a subject specific headmodel and sourcemodel, as explained in the head- and sourcemodel tutorial.

This tutorial will not cover the frequency-domain option for DICS/PCC beamformers (which is explained here), nor how to compute minimum-norm-estimated sources of evoked/averaged data (which is explained here).

Procedure

To localise the evoked sources for this example dataset we will perform the following steps:

• Read the data into MATLAB using the same strategy as in the raw2erp tutorial.
• Spatially whiten the data to account for differences in sensor type (magnetometers versus gradiometers) with ft_denoise_prewhiten
• Compute the covariance matrix using the function ft_timelockanalysis.
• Construct the leadfield matrix using ft_prepare_leadfield, in combination with the previously computed head- and sourcemodels + the whitened gradiometer array.
• Compute a spatial filter and estimate the amplitude of the sources using ft_sourceanalysis
• Visualize the results, using ft_sourceplot_interactive.

Preprocessing

Reading the data, and some issues with covariance matrices

The aim is to reconstruct the sources underlying the event-related field, when the subject is presented with pictures of faces. in the raw2erp tutorial we have computed sensor-level event-related fields, but we also stored the single-epoch data. We start off by loading the precomputed single-epoch data, and the headmodel and sourcemodel that were created during the anatomy tutorial.

subj = datainfo_subject(15);
filename = fullfile(subj.outputpath, 'raw2erp', subj.name, sprintf('%s_data', subj.name));
load(filename, 'data');

In this tutorial, we are only going to use the MEG data for the source reconstruction. Therefore, we proceed by selecting the MEG channels from the epoched data.

cfg         = [];
cfg.channel = {'MEG'};
data        = ft_selectdata(cfg, data);

Next, for reasons that will become clear soon, we also select from the epoched data the timewindows just preceding the onset of the stimulus, from a time window between -200 ms and 0.

cfg         = [];
cfg.latency = [-0.2 0];
baseline    = ft_selectdata(cfg, data);

Next, we use ft_timelockanalysis to compute the sensor-level covariance of the baseline data.

cfg            = [];
cfg.covariance = 'yes';
baseline_avg   = ft_timelockanalysis(cfg, baseline);

Now, if we reorder the channels a bit, we can visualise this covariance matrix as follows:

selmag  = ft_chantype(baseline_avg.label, 'megmag');
selgrad = ft_chantype(baseline_avg.label, 'megplanar');

C = baseline_avg.cov([find(selmag);find(selgrad)],[find(selmag);find(selgrad)]);
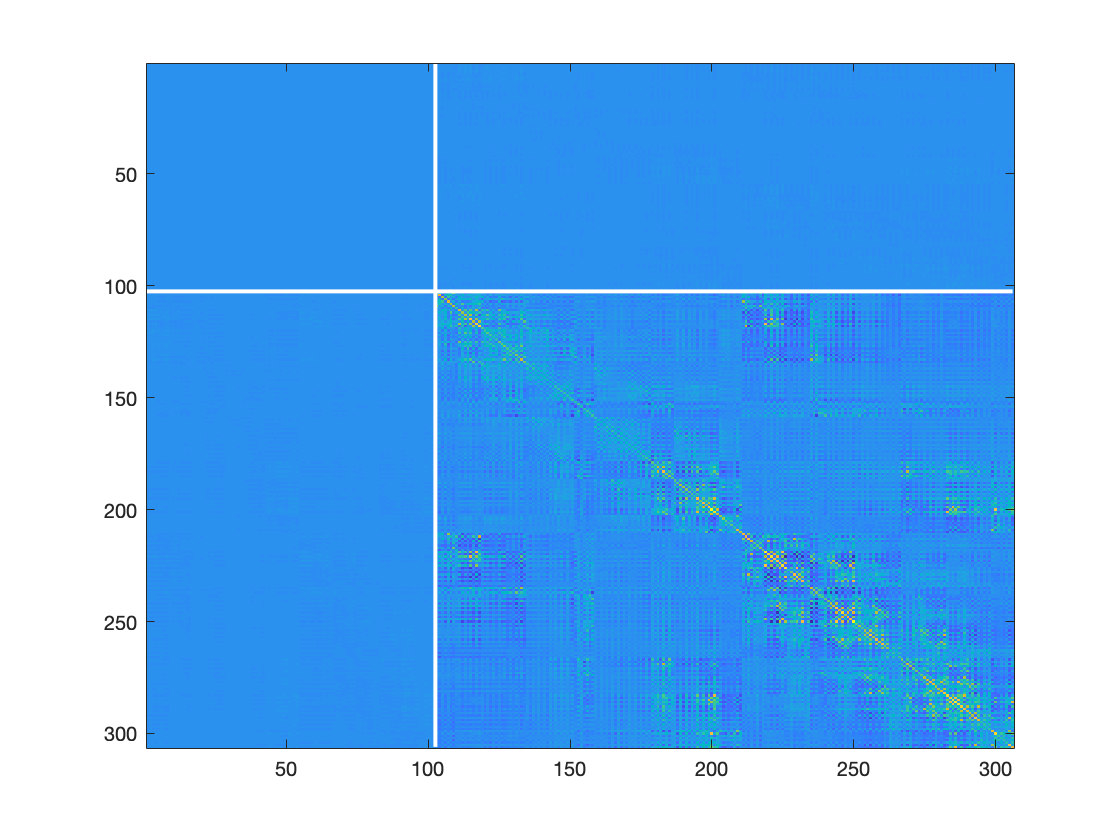
figure;imagesc(C);hold on;plot(102.5.*[1 1],[0 306],'w','linewidth',2);plot([0 306],102.5.*[1 1],'w','linewidth',2);

Figure: MEG sensor covariance matrix

The figure shows the covariance between all pairs of magnetometers in the left upper square on the diagonal, between all pairs of gradiometers the right lower square, and the covariance between magnetometers and gradiometers in the off- diagonal blocks. As can be seen, the left upper and off-diagonal blocks appear blue, suggesting that the numerical range of the magnetometer is a lot smaller than the numerical range of the gradiometers. In itself, this might not pose a problem, but it will result in a different weighing of gradiometers versus magnetometers when computing the source reconstruction. In addition to the difference in magnitude of the different channel types, the covariance matrix may be poorly estimated (for instance due to a limited amount of data available), or may be rank deficient due to previous processing steps. Examples of processing steps that cause the data to be rank deficient are artifact cleaning procedures based on independent component analysis (ICA), or signal space projections (SSPs). Another important processing step that reduces the rank of the data massively, is Elekta’s maxfilter.

It is crucial to account for rank deficiency of the data, because if it’s not done properly, the noise (be it numerical or real) will blow up the reconstruction. Beamformers require the mathematical inverse of the covariance matrix computed from the epochs-of-interest (typically including a baseline window but never computed on the baseline window alone). State-of-the-art distributed source reconstuction with minimum-norm estimation (MNE) require (implicitly) the mathematical inverse of a noise covariance matrix. Either way, irrespective of your favourite source reconstruction method, mathematical inversion of rank deficient covariance matrices that moreover consist of signals with different orders of magnitude requires some tricks to make the final result numerically well-behaved. To make this a bit more concrete, we first will have a look at the singular value decomposition (which in this case is similar to a principal component analysis) of the baseline covariance matrix:

[u,s,v] = svd(baseline_avg.cov);
figure;plot(log10(diag(s)),'o');

Figure: Singular values of a MEG sensor covariance matrix

When thus plotted on a log scale, it can be seen that there is a range of 16 orders of magnitude in the signal components, and that there are actually 3 stairs in this singular value spectrum. There is a steep decline around component 70 or so, and another step at component 204. The step at component 204 reflects the magnitude difference between the 204 gradiometer signals and the 102 magnetometer signals. The discontinuity around component 70 reflects the effect of the Maxfilter, which has effectively removed about 236 spatial components out of the data.

Just using the ‘normal’ way of computing the covariance matrix’ inverse, by using MATLAB’s inv() function is asking for numerical problems, because the spatial components with very small singular values (which don’t reflect any real signal) are blown up big time in the inverse. For this reason, regularised or truncated inversion techniques are to be used. In addition to applying more thoughtful algorithms for matrix inversion, spatial prewhitening techniques can be used, which manipulate the data in a way to make them, as the name suggests, spatially (more or less) white. This means that the signals are uncorrelated to each other, and have the same variance. As a byproduct, when the whitening is done separately for the magnetometers and gradiometers, the scale difference between the different channel types disappears, and thus prewhitening results in an ‘equal’ treatment of both channel types, and allows for a relatively straightforward combination of the different channel types during source reconstruction.

Spatial whitening of the task data, using the activity from the baseline

The function ft_denoise_prewhiten can be used for the prewhitening. As an input, it requires a data structure of the to-be-prewhitened data, and a data structure that contains a covariance structure that is used for the computation of the prewhitening operator. For MEG data, one can use an empty room recording for this, or a data structure containing data from a well-defined baseline window. Here, we use the 200 ms time window prior to the onset of the stimulus. In its default behaviour, ft_denoise_prewhiten does a separate prewhitening of the different channeltypes in the input data, so the magnetometers and gradiometers will be prewhitened separately.

% the following lines detect the location of the first large 'cliff' in the singular value spectrum of the grads and mags
[u,s_mag,v]  = svd(baseline_avg.cov(selmag,  selmag));
[u,s_grad,v] = svd(baseline_avg.cov(selgrad, selgrad));
d_mag = -diff(log10(diag(s_mag))); d_mag = d_mag./std(d_mag);
kappa_mag = find(d_mag>4,1,'first');
d_grad = -diff(log10(diag(s_grad))); d_grad = d_grad./std(d_grad);
kappa_grad = find(d_grad>4,1,'first');

cfg            = [];
cfg.channel    = 'meg';
cfg.kappa      = min(kappa_mag,kappa_grad);
dataw_meg      = ft_denoise_prewhiten(cfg, data, baseline_avg);

The prewhitening operator is defined as the inverse of the matrix square root of the covariance matrix that is to be used for the prewhitening. The cfg.kappa option in ft_denoise_prewhiten ensures that a regularised inverse is used. Kappa refers to the number of spatial components to be retained in the inverse, and should be at most the number before which the steep cliff in singular values occurs.

Exercise 1

A byproduct of the magnetometers and gradiometers being represented at a similar scale, is the possibility to do a quick-and-dirty artifact identification (and rejection) using ft_rejectvisual.

cfg        = [];
cfg.layout = 'neuromag306mag_helmet.mat';
layout     = ft_prepare_layout(cfg);

cfg        = [];
cfg.method = 'summary';
cfg.layout = layout;
dataw_meg  = ft_rejectvisual(cfg, dataw_meg);

Figure: Visual artifact rejection window

Exercise 2

Computation of the covariance matrix of the prewhitened data

For a beamformer analysis, we need to compute the covariance between all pairs of channels during a time window of interest, which should include the active time window, i.e. the time window after stimulus onset. Thus, we should not constrain the window to the prestimulus time window, as we have done so far. The covariance, as an average across all single trial covariances is computed by using ft_timelockanalysis on the prewhitened data, including the whole time window (i.e. we don’t call ft_selectdata to extract a time window from the data):

cfg = [];
cfg.preproc.demean = 'yes';
cfg.preproc.baselinewindow = [-0.2 0];
cfg.covariance = 'yes';
tlckw = ft_timelockanalysis(cfg, dataw_meg);

Computation of the forward model

For a beamformer analysis, we need to predefine a set of dipole locations to be scanned. Typically, this set of dipole locations is defined on a 3D grid, to allow for volumetric postprocessing possibilities (for instance volumetric spatial normalisation for group statistics). Alternatively, we can use a set of dipole locations defined on the cortical sheet, e.g., as per the sourcemodel created in the head- and sourcemodel tutorial. With the surface-based models being registered to a template, postprocessing is relatively straightforward. Moreover, parcellation of the source reconstructed results using surface-based atlases can be easily achieved.

Finally, with the beamformer solution on the cortical surface, it can be easily compared to a MNE solution, should one be inclined to do so. It is important to note that 1) the metric units of the geometric objects are identical to one another, and 2) to use here the gradiometer array from the whitened data, because we will also use the whitened data for the source reconstruction. With respect to point 1, FieldTrip will check for this, but to be sure, we ensure the equality of metric units explicitly.

% obtain the necessary ingredients for obtaining a forward model
load(fullfile(subj.outputpath, 'anatomy', subj.name, sprintf('%s_headmodel', subj.name)));
load(fullfile(subj.outputpath, 'anatomy', subj.name, sprintf('%s_sourcemodel', subj.name)));
headmodel   = ft_convert_units(headmodel,   tlckw.grad.unit);
sourcemodel = ft_convert_units(sourcemodel, tlckw.grad.unit);
sourcemodel.inside = sourcemodel.atlasroi>0;

% compute the forward model for the whitened data
cfg             = [];
cfg.channel     = tlckw.label;
cfg.grad        = tlckw.grad; % NOTE: input of the whitened data ensures the correct sensor definition to be used
cfg.sourcemodel = sourcemodel;
cfg.headmodel   = headmodel;
cfg.method      = 'singleshell';
cfg.singleshell.batchsize = 1000;
leadfield_meg   = ft_prepare_leadfield(cfg);

Source analysis and visualisation of virtual channel data

With the forward model and the covariance (as average across trials) computed, we can proceed with the computation of the beamformer solution. For this, we need to specify a kappa parameter for the regularisation. Also, we will specify that the spatial filters be kept in the output, so that we can later apply them to the individual conditions, in order to obtain condition-specific event-related averages at the source level, ensuring that the same spatial filter is used for each condition. Also, we specify the spatial filter to have a ‘fixedori’, which means that for each dipole location the source is assumed to have a fixed orientation.

[u,s,v] = svd(tlckw.cov);
d       = -diff(log10(diag(s)));
d       = d./std(d);
kappa   = find(d>5,1,'first');

cfg                 = [];
cfg.method          = 'lcmv';
cfg.lcmv.kappa      = kappa;
cfg.lcmv.keepfilter = 'yes';
cfg.lcmv.fixedori   = 'yes';
cfg.lcmv.weightnorm = 'unitnoisegain';
cfg.headmodel       = headmodel;
cfg.sourcemodel     = leadfield_meg;
source              = ft_sourceanalysis(cfg, tlckw);

filename = fullfile(subj.outputpath, 'sourceanalysis', subj.name,  sprintf('%s_source_lcmv', subj.name));
save(filename, 'source', 'tlckw');

With the source structure computed, we can inspect the fields of the variable source, and the subfields of source.avg:

>> source

source =
  struct with fields:
      time: [1x510 double]
    inside: [15684x1 logical]
       pos: [15684x3 double]
       tri: [31360x3 double]
    method: 'average'
       avg: [1x1 struct]
       cfg: [1x1 struct]

>> source.avg

ans =
struct with fields:
             ori: {1x15684 cell}
             pow: [15684x1 double]
             mom: {15684x1 cell}
           noise: [15684x1 double]
          filter: {15684x1 cell}
           label: {306x1 cell}
    filterdimord: '{pos}_ori_chan'

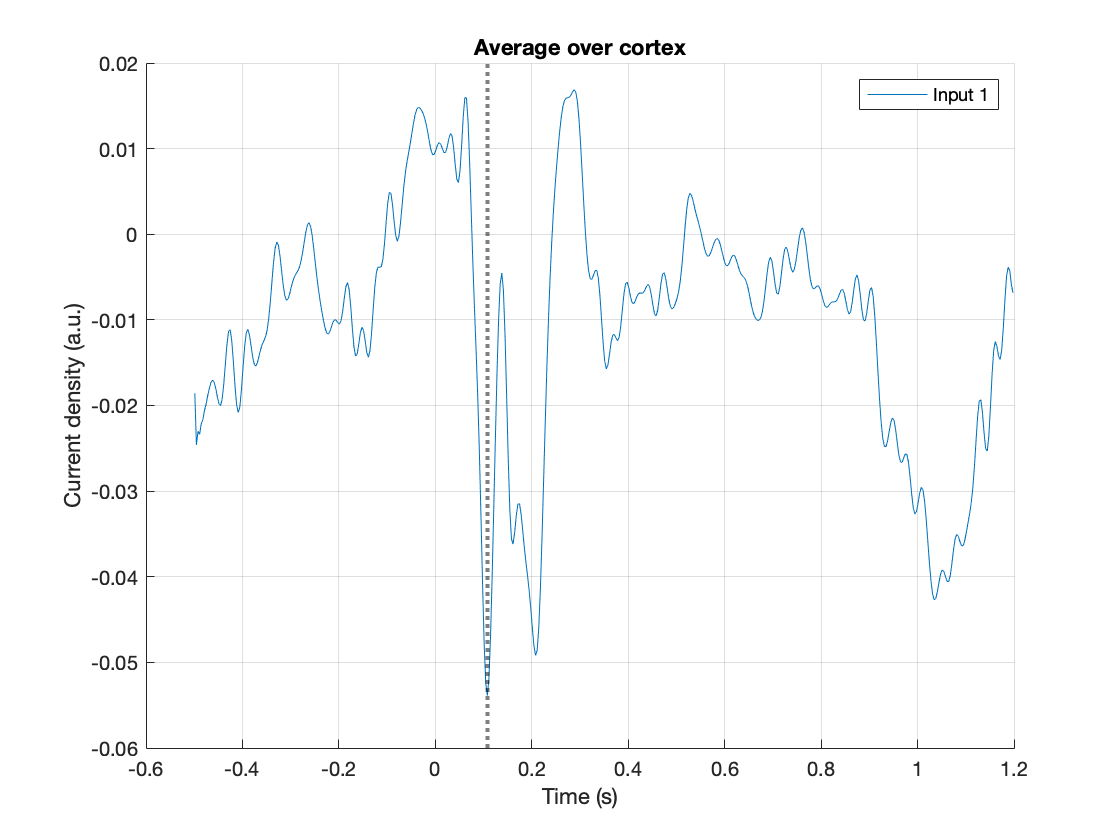
The content of source.avg is the interesting stuff. Particularly, the mom field contains the time courses of the event-related field at the source level. Colloquially, these time courses are known as ‘virtual channels’, reflecting the signal that would be picked up if it could directly be recorded by a channel at that location. The pow field is a scalar per dipole position, and reflects the variance over the time window of interest, and typically does not mean much for an LCMV beamformer. The field filter contains the beamformer spatial filter, which we will be using in a next step, in order to extract condition specific data. First, we will now inspect the virtual channels using ft_sourceplot_interactive.

wb_dir   = fullfile(subj.outputpath, 'anatomy',subj.name, 'freesurfer', subj.name, 'workbench');
filename = fullfile(wb_dir, sprintf('%s.L.inflated.8k_fs_LR.surf.gii', subj.name));
inflated = ft_read_headshape({filename strrep(filename, '.L.', '.R.')});
inflated = ft_determine_units(inflated);
inflated.coordsys = 'neuromag';

cfg           = [];
cfg.clim      = [-1 1];
cfg.colormap  = '-RdBu';
cfg.parameter = 'mom';

% replace the original dipole positions with those of the inflated surface
source.pos = inflated.pos;
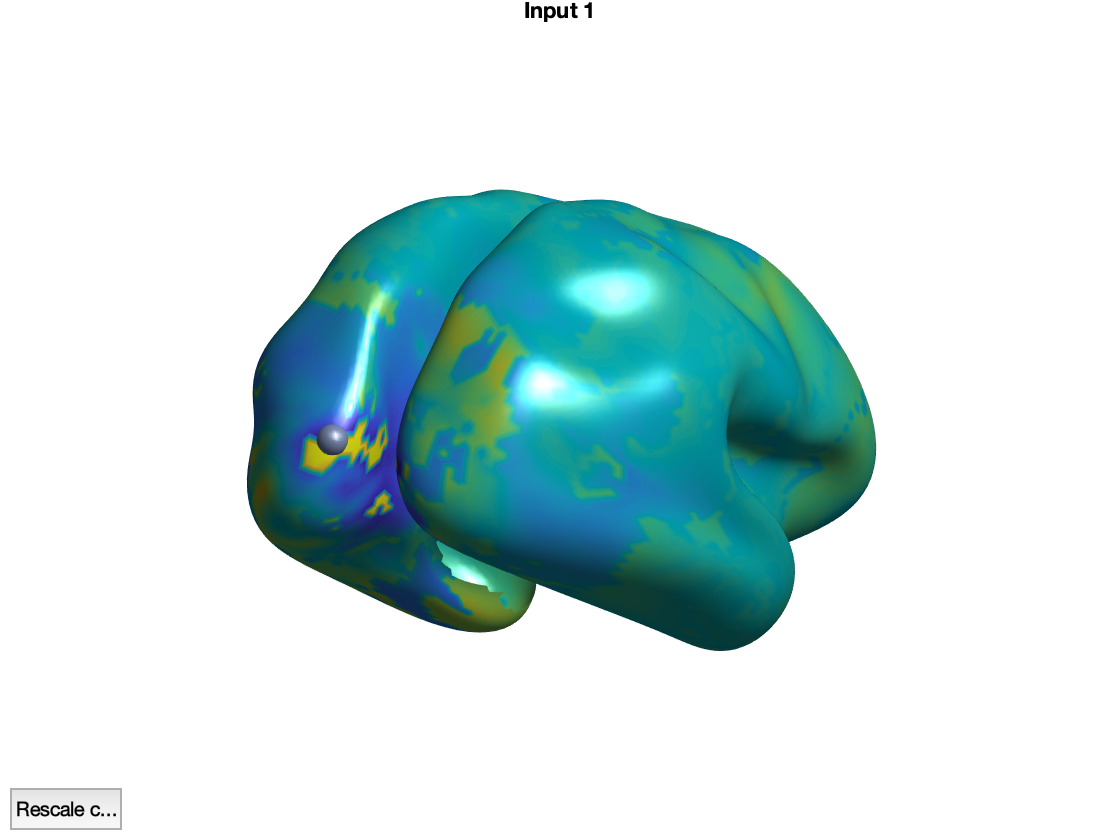
ft_sourceplot_interactive(cfg, source);

Figure: Interactive figure windows to inspect virtual channels

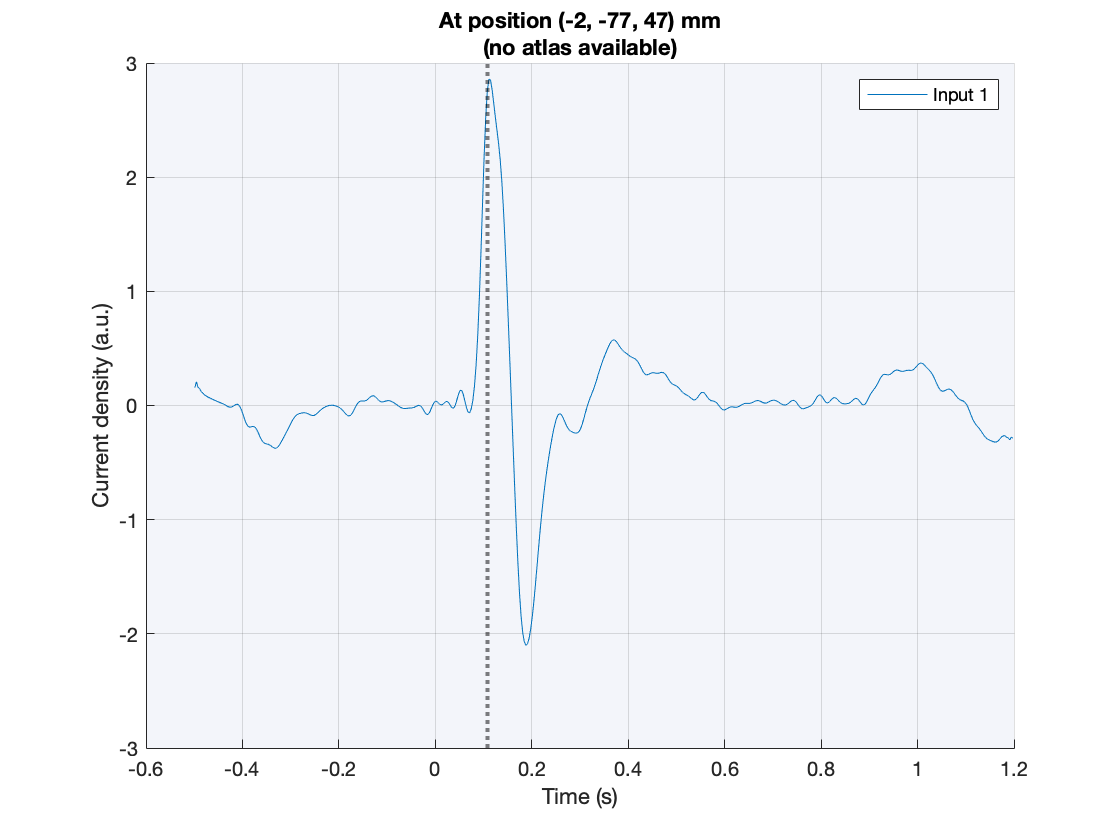
The function ft_sourceplot_interactive opens two figures, one showing a time course with the event-related field, averaged across all dipoles, and the other showing the cortical surface. Here, we replaced the original cortical sheet dipole positions with their equivalent ‘inflated’ counterparts to better appreciate the stuff that is going on in the sulci. Pressing the shift-key while selecting a location on the cortical surface creates a new figure, with the event-related field of the selected location. Clicking in the figure with the time courses shifts the latency at which the corresponding topographical map is shown.

Exercise 3

Exercise 4

cfg = [];
cfg.operation = 'abs';
cfg.parameter = 'mom';
sourceabsmom  = ft_math(cfg, source);

Source analysis and visualisation of virtual channel data per condition

With the spatial filters computed from the covariance matrix estimated from all trials combined, we can now proceed to estimate the per condition ERFs.

cfg                = [];
cfg.preproc.baselinewindow = [-0.2 0];
cfg.preproc.demean = 'yes';
cfg.covariance     = 'yes';

% this is what we can see in the BIDS events.tsv file
Famous      = [5 6 7];
Unfamiliar  = [13 14 15];
Scrambled   = [17 18 19];

cfg.trials = ismember(dataw_meg.trialinfo(:,1), Famous);
tlckw_famous = ft_timelockanalysis(cfg, dataw_meg);

cfg.trials = ismember(dataw_meg.trialinfo(:,1), Unfamiliar);
tlckw_unfamiliar = ft_timelockanalysis(cfg, dataw_meg);

cfg.trials = ismember(dataw_meg.trialinfo(:,1), Scrambled);
tlckw_scrambled = ft_timelockanalysis(cfg, dataw_meg);

cfg                 = [];
cfg.method          = 'lcmv';
cfg.lcmv.kappa      = kappa;
cfg.lcmv.keepfilter = 'yes';
cfg.lcmv.fixedori   = 'yes';
cfg.lcmv.weightnorm = 'unitnoisegain';
cfg.headmodel       = headmodel;
cfg.sourcemodel     = leadfield_meg;
cfg.sourcemodel.filter       = source.avg.filter;
cfg.sourcemodel.filterdimord = source.avg.filterdimord;
source_famous_orig     = ft_sourceanalysis(cfg, tlckw_famous);
source_unfamiliar_orig = ft_sourceanalysis(cfg, tlckw_unfamiliar);
source_scrambled_orig  = ft_sourceanalysis(cfg, tlckw_scrambled);

cfg = [];
cfg.operation = 'abs';
cfg.parameter = 'mom';
source_famous = ft_math(cfg, source_famous_orig);
source_unfamiliar = ft_math(cfg, source_unfamiliar_orig);
source_scrambled  = ft_math(cfg, source_scrambled_orig);

cfg           = [];
cfg.parameter = 'mom';
cfg.colormap  = '-RdBu';
cfg.clim      = [-1 1];
ft_sourceplot_interactive(cfg, source_famous, source_unfamiliar, source_scrambled);

You can also investigate the difference between the ‘famous’ and ‘scrambled’ conditions:

cfg = [];
cfg.operation = 'subtract';
cfg.parameter = 'mom';
cfg.colormap  = '-RdBu';
cfg.clim      = [-1 1];
source_diff   = ft_math(cfg, source_famous, source_scrambled);

cfg           = [];
cfg.parameter = 'mom';
cfg.has_diff  = true;
cfg.clim      = [-1 1];
ft_sourceplot_interactive(cfg, source_famous, source_scrambled, source_diff);