Irregular Resampling Auto-Spectral Analysis (IRASA)
IRASA allows distinguishing rhythmic activity from concurrent power-spectral 1/f modulations. The technique virtually compresses and expands the time-domain data with a set of non-integer resampling factors prior to Fourier-based spectral decomposition. As a result, rhythmic components in the power-spectrum are redistributed while the arrhythmic 1/f distribution is left intact. Taking the median of the resulting auto-spectral distributions extracts the power-spectral 1/f component, and the subsequent removal of the 1/f component from the original power-spectrum offers a power-spectral estimate of rhythmic content in the recorded signal. Below we provide two examples, a simulated dataset and a real human ECoG dataset (Stolk et al. 2019), including how to extract spectral features based on the IRASA technique (Wen & Liu, 2016).
Extracting spectral features of simulated data
% set simulation parameters
A = 1; % scale of 1/f amplitude
C = 1; % 1/f slope
O = 1; % weight of oscillatory components of the simulated data
lf = 1; % lower bound of freq
hf = 300; % higher bound of freq
sl = 600; % spectral lines
fs = 1000; % sampling rate
n = 60000; % time pnts
t = (1:n)/fs; % time axis
% simulate data
for rpt = 1:1
% simulate fractal component
freq = linspace(lf, hf, sl); % sampling frequesies
fn = zeros(size(t));
for i=1:length(freq) % cummulative sum over freq
fn = fn + (A * 1/freq(i)^C) * cos(2*pi*freq(i)*t + rand*2*pi); % 1/f amplitude = a*(1/f^c)
end
% simulate a 10Hz and 60 Hz oscillatory component
data.trial{1,rpt} = fn + O * cos(2*pi*10*t) + O * cos(2*pi*60*t);
data.time{1,rpt} = t;
data.label{1} = 'chan';
data.trialinfo(rpt,1) = rpt;
end
% chunk 2-second segments (gives 1Hz frequency resolution) for long/continuous trials
cfg = [];
cfg.length = 2; % freqency resolution = 1/2^floor(log2(cfg.length*0.9))
cfg.overlap = 0.5;
data = ft_redefinetrial(cfg, data);
% compute the fractal and original spectra
tic
cfg = [];
cfg.foilim = [1 200];
cfg.pad = 'nextpow2';
cfg.method = 'irasa';
cfg.output = 'fractal';
fractal = ft_freqanalysis(cfg, data);
cfg.output = 'original';
original = ft_freqanalysis(cfg, data);
toc % ~28s
% subtract the fractal component from the power spectrum
cfg = [];
cfg.parameter = 'powspctrm';
cfg.operation = 'x2-x1';
oscillatory = ft_math(cfg, fractal, original);
% display the spectra in log-log scale
figure();
hold on;
plot(log(original.freq), log(original.powspctrm),'k');
plot(log(fractal.freq), log(fractal.powspctrm));
plot(log(fractal.freq), log(oscillatory.powspctrm));
xlabel('log-freq'); ylabel('log-power');
legend({'original','fractal','oscillatory'},'location','southwest');
if A~=0 && O==0
title('pure fractal signal');
elseif A==0 && O~=0
title('pure oscillatory signal');
elseif A~=0 && O~=0
title('mixed signal');
end
Extracting spectral features from human ECoG data
Now we will work on the example of a ECoG dataset (Stolk et al. 2019). This adaptive approach allows defining rhythm frequency bands on a participant-by-participant basis (e.g., alpha and beta frequency bands), avoiding having to rely on canonical frequency bands that may not accurately capture the neural phenomena of interest in each individual. To run this example, download S5_raw_segmented.mat from the OSF repository. Additionally, download S5_lh.pial used to localize rhythmic activity in the sensorimotor cortex in a next step.
- Read in and preprocess the data
% load the raw raw data
load('S5_raw_segmented.mat')
% filter and re-reference the raw data
cfg = [];
cfg.hpfilter = 'yes';
cfg.hpfiltord = 3;
cfg.hpfreq = 1;
cfg.lpfilter = 'yes';
cfg.lpfiltord = 3;
cfg.lpfreq = 249;
cfg.bsfilter = 'yes';
cfg.bsfiltord = 3;
cfg.bsfreq = [49 51; 99 101; 149 151; 199 201]; % EU line noise
cfg.reref = 'yes';
cfg.refchannel = 'all';
data_filt = ft_preprocessing(cfg, data);
% select electrodes placed over the sensorimotor cortex
cfg = [];
cfg.channel = {'chan007','chan008','chan015','chan016','chan024', ...
'chan092','chan093','chan094','chan095', ...
'chan113','chan115','chan117','chan118','chan119'};
data_sel = ft_selectdata(cfg, data_filt);
- Run IRASA with sliding window for the continuous recording
% segment the data into one-second overlapping chunks
cfg = [];
cfg.length = 1;
cfg.overlap = .95; % 95 percent overlap (sliding 50 ms)
data_redef = ft_redefinetrial(cfg, data_sel);
% compute the fractal and original spectra
cfg = [];
cfg.foilim = [1 50];
cfg.pad = 'nextpow2';
cfg.method = 'irasa';
cfg.output = 'fractal';
fractal = ft_freqanalysis(cfg, data_redef);
cfg.output = 'original';
original = ft_freqanalysis(cfg, data_redef);
% subtract the fractal component from the power spectrum
cfg = [];
cfg.parameter = 'powspctrm';
cfg.operation = 'x2-x1';
oscillatory = ft_math(cfg, fractal, original);
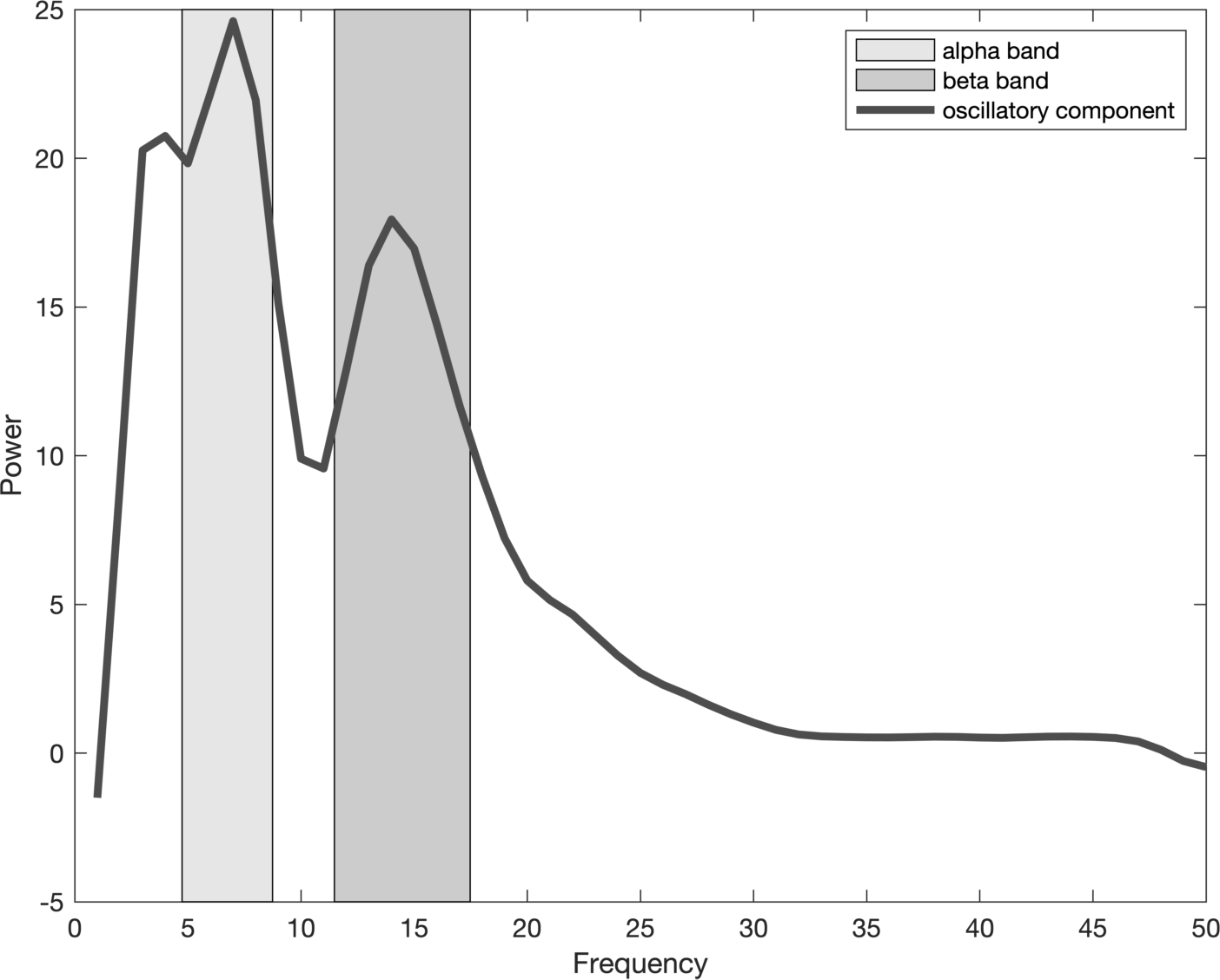
% extract alpha and beta frequency bands
figure;
plot(oscillatory.freq, mean(oscillatory.powspctrm), ...
'linewidth', 3, 'color', [.3 .3 .3])
f = fit(oscillatory.freq', mean(oscillatory.powspctrm)', 'gauss3');
alpha_band = [f.b1-2 f.b1+2];
beta_band = [f.b3-3 f.b3+3];
yl = get(gca, 'YLim');
p1 = patch([alpha_band flip(alpha_band)], [yl(1) yl(1) yl(2) yl(2)], [.9 .9 .9]);
p2 = patch([beta_band flip(beta_band)], [yl(1) yl(1) yl(2) yl(2)], [.8 .8 .8]);
uistack(p2, 'bottom'); uistack(p1, 'bottom');
legend('alpha band', 'beta band', 'oscillatory component');
xlabel('Frequency'); ylabel('Power');
set(gca, 'YLim', yl);
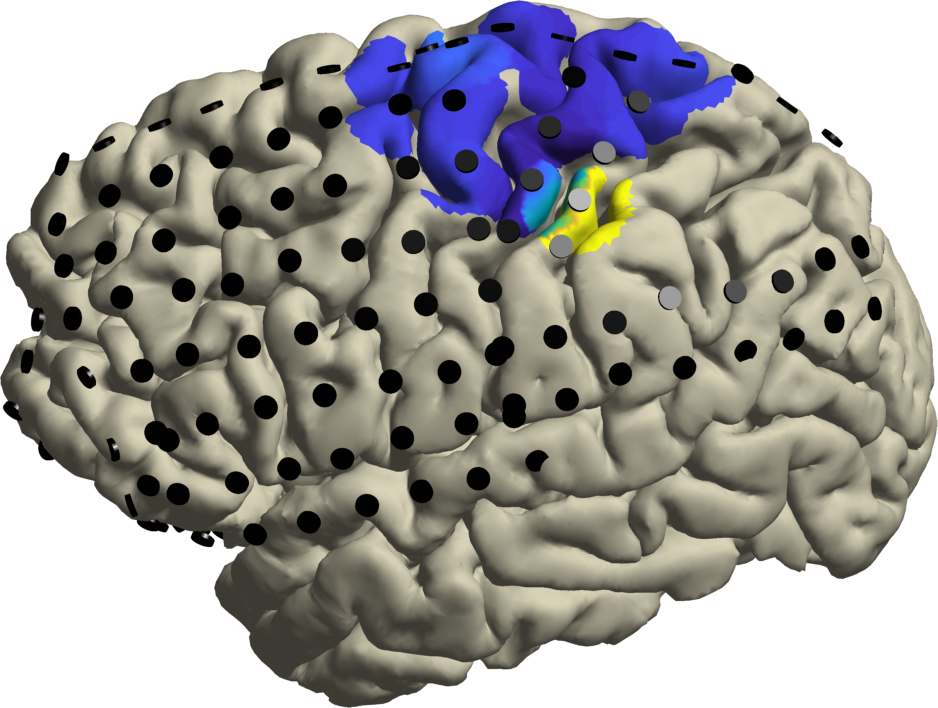
- Localizing spectral features in the sensorimotor cortex
% read in the cortical surface
cortex = ft_read_headshape('S5_lh.pial');
% plot the spatial distribution of alpha rhythmic activity
cfg = [];
cfg.frequency = alpha_band;
cfg.avgoverfreq = 'yes';
alpha = ft_selectdata(cfg, oscillatory);
cfg = [];
cfg.funparameter = 'powspctrm';
cfg.funcolorlim = 'zeromax';
cfg.method = 'surface';
cfg.interpmethod = 'sphere_weighteddistance';
cfg.sphereradius = 10;
cfg.camlight = 'no';
cfg.funcolormap = 'parula';
cfg.colorbar = 'no';
ft_sourceplot(cfg, alpha, cortex);
view([-90 20]);
material dull; lighting gouraud; camlight
ft_plot_sens(alpha.elec, 'elecshape', 'disc', 'facecolor', [0 0 0])
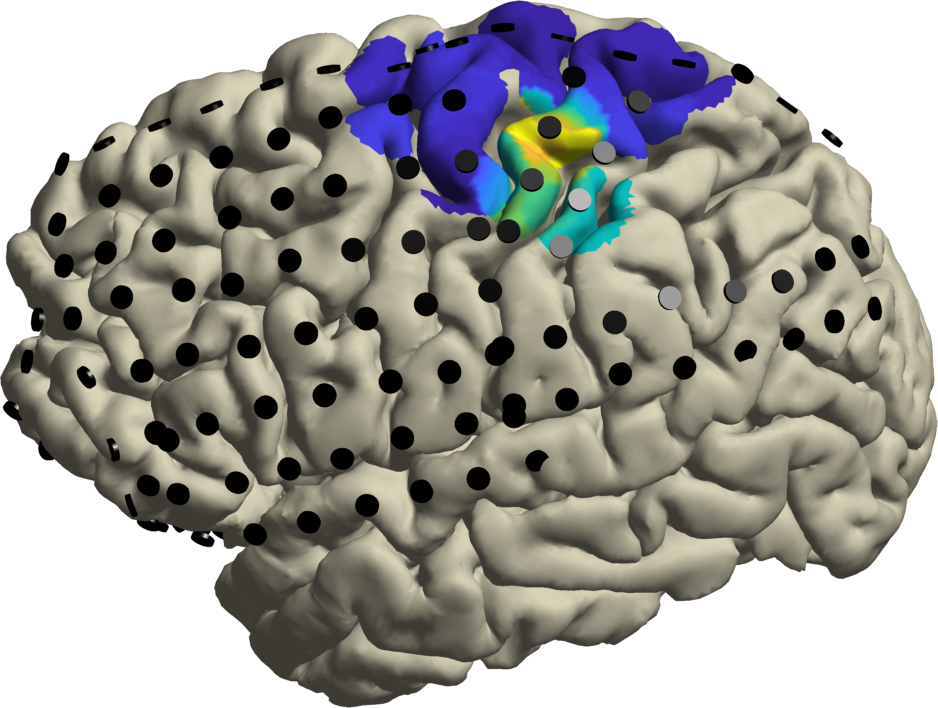
% plot the spatial distribution of beta rhythmic activity
cfg = [];
cfg.frequency = beta_band;
cfg.avgoverfreq = 'yes';
beta = ft_selectdata(cfg, oscillatory);
cfg = [];
cfg.funparameter = 'powspctrm';
cfg.funcolorlim = 'zeromax';
cfg.method = 'surface';
cfg.interpmethod = 'sphere_weighteddistance';
cfg.sphereradius = 10;
cfg.camlight = 'no';
cfg.funcolormap = 'parula';
cfg.colorbar = 'no';
ft_sourceplot(cfg, beta, cortex);
view([-90 20]);
material dull; lighting gouraud; camlight
ft_plot_sens(beta.elec, 'elecshape', 'disc', 'facecolor', [0 0 0])
Consistent with (Stolk et al. 2019), alpha rhythmic activity is maximal at electrodes on the postcentral gyrus, and beta rhythmic activity is strongest at electrodes placed over the central sulcus.
Updates to the IRASA implementation
Starting from version 20210114 the implementation of ft_specest_irasa has been changed. The current implementation corrects the computational order of geometric and arithmetic means for estimating the fractal power-spectrum (Wen & Liu, 2016), which were swapped in the previous implementation (see issue 1546).
If you have used the previous implementation of IRASA, we recommend you to adapt your analysis script according the the following points:
-
The current implementation enables IRASA and FFT for estimating both the fractal and original power-spectra, respectively. You do not have to use cfg.method=’mtmfft’ any more for computing the original power-spectrum. We recommend to compute both of them with cfg.method=’irasa’ to ensure a consistent frequency resolution and tapering of the fractal and original power-spectra. For that you should call ft_freqanalysis twice, once with cfg.output=’fractal’, and once with cfg.output=’original’.
-
The current implementation partition the trials automatically, so you do not have to call ft_redefinetrial. However, if you are analyzing a continuous trial or trials with unequal length, it is recommended to segment the data following the Welch’s method before spectrum estimation, as illustrated in the example scripts above. The frequency resolution of the output will be
fs/2^floor(log2(L*fs*0.9))where L is the length of the segments in seconds and fs refers to the sampling rate.
Note that the upper limit of cfg.foilim has to be specified 1.9 (the maximal resampling factor of IRASA) times as large as your intent, due to the resampling procedure of IRASA. For instance, you are interested in 100 Hz, the upper limit shall be set as 1.9 * 100 = 190 Hz. The same logic holds when you apply IRASA onto a band-pass or low-pass filtered dataset. Keep in mind, the filters might be done with your own analysis piplines and/or with the acquisition system itself. For example, MEG data acquired at the Donders Centre for Cognitive Neuroimaging (DCCN) with standard acquisition settings at 1200 Hz will have been subjected to a 300 Hz low-pass filter.