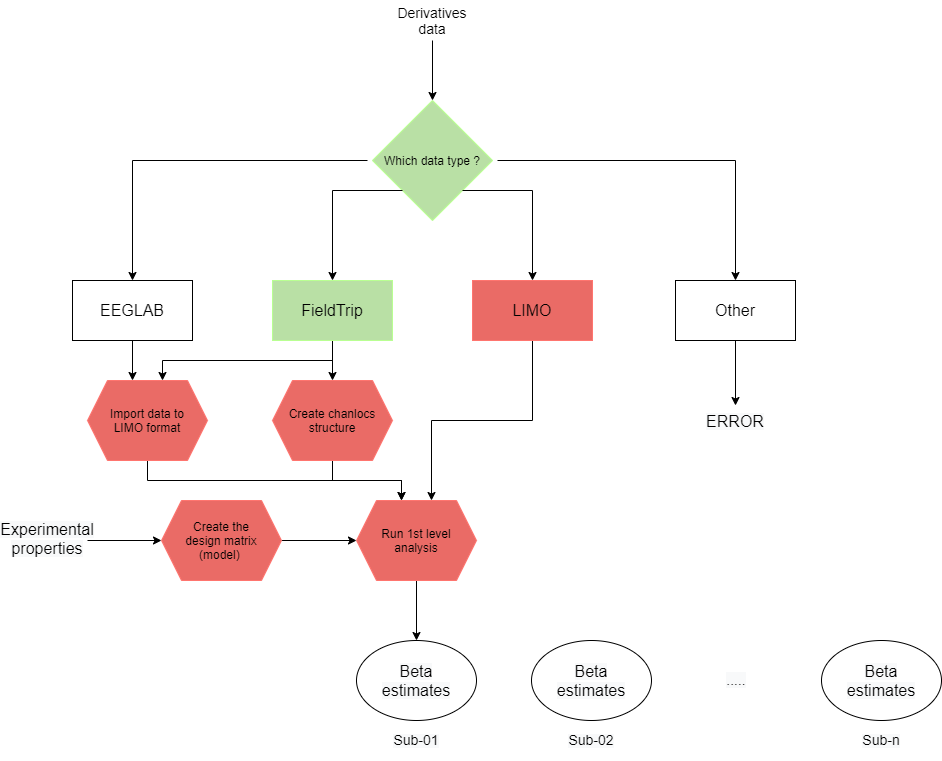
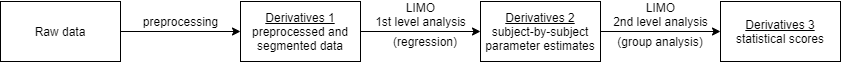Getting started with LIMO EEG

Background

LIMO MEEG is an open source toolbox for statistical analysis of MEEG data (Pernet et al., 2011). The main goal of the toolbox is to provide ‘full space’ analyses of experimental effects, i.e. simultaneously for all time and/or frequency time points and all channels, independent components or sources. It is implemented in MATLAB and requires the MathWorks statistics and machine learning toolbox.

LIMO tools rely on a hierarchical general linear model (GLM), accounting for within-subject variance (single trial analyses) and between-subject variance. There are a large range of statistical features:

• for estimation: ordinary least squares, trial weighted least squares, trimmed means
• for testing: t-tests, linear regressions, ANOVAs, ANCOVAs, repeated measures ANOVA.
• for inference: spatiotemporal clustering, threshold free cluster enhancement, maximum statistics (multiple comparisons correction)

The following figure illustrates the hierarchical analysis consisting of a 1st-level estimation of a GLM regression model and a 2nd-level statistical test of specific contrasts:

LIMO was initially designed as a plug-in of EEGLAB, but more recent versions are also compatible with FieldTrip raw and source data. Statistical analyses can be performed on other data representations, but that requires some manual reformatting of the data structures.

Although LIMO is primarily designed for EEG data, it can also process MEG and iEEG data.

Data format

As LIMO directly reads and writes data from/to disk, the recommended way to organize the input data is through Brain Imaging Data Structure (BIDS) standard. This standard aims to organize neuroimaging data in a uniform way to simplify data sharing through the scientific community. More background on BIDS and example datasets can be found here.

The inputs of LIMO consists of preprocessed and segmented data (EEG or source-level time series) that are stored as .mat (FieldTrip data) or .set (EEGLAB data) files. Following BIDS standard, those data are known as derivatives data.

The outputs of LIMO are generated at each levels:

1. First level analysis derives subject specific parameter estimates (n_channels x n_timeframes x n_variables matrix) for any effects as well as contrast estimates (n_channels x n_timeframes x n_stat_variables matrix).
2. Second level analysis results of a n_channels x n_timeframes x n_stat_variables matrix corresponding to the group analysis.

The following outline shows the BIDS raw data and derivatives structure that represents the pipeline inputs and outputs, going from raw -> preproc -> timelock -> LIMO 1st level -> LIMO 2nd level analysis:

dataset/
├── dataset_description.json
├── participants.tsv
├── README
├── CHANGES
├── sub-01
│   └── eeg
│       ├── sub-01_task-xxx.vhdr
│       ├── sub-01_task-xxx_eeg.vmrk
│       ├── sub-01_task-xxx_eeg.eeg
│       ├── sub-01_task-xxx_eeg.json
│       └── sub-01_task-xxx_events.tsv
├── sub-02
├── ...
├── derivatives
│   └── preproc_and_segment
│       ├── dataset_description.json
│       ├── sub-01
│       │   └── eeg
│       │       ├── sub-01_timelock.mat
│       │       └── sub-01_timelock.json
│       ├── sub-02
│       ├── ...
│       ├── derivatives
│       │   └── 1st_level
│       │       ├── dataset_description.json
│       │       │   └── limo
│       │       │       ├── sub-01_betas.mat
│       │       │       ├── sub-01_con_1.mat
│       │       │       └── ...
│       │       ├── sub-01
│       │       ├── sub-02
│       │       ├── ...
│       │       ├── derivatives
│       │       │   └── one_sample_t_test
│       │       │       ├── dataset_description.json
│       │       │       ├── one_sample_t_test_parameter_1.mat
│       │       │       └── ...

How does LIMO use FieldTrip?

LIMO integrates with some FieldTrip functions to deal with FieldTrip data structures. The ft_datatype function is used to determine the type of data structure in the .mat file, ensures that the data structure is valid and that it has the required fields. Subsequently, LIMO convert the data to its appropriate low-level format. The following figure illustrates this process:

After having estimated the betas with the 1st-level analysis, LIMO continues with the 2nd-level (group level) analysis.

Global framework

Processing data through FieldTrip functions and performing statistical analyses on the processed data in LIMO is easy. The users can specify the experimental design (the GLM model) and the FieldTrip data as input. Using BIDS raw and derived data, the whole pipeline going from raw data, preprocessing, 1st-level analysis and 2nd-level testing, can be considered as follows:

The example that follows uses the EEG of the multimodal Wakeman & Henson (2015) dataset. This data is acquired during visual stimulation with 3 face categories (famous, unknown and scrambled) and 1 covariate (the time between the first and the second repeated presentation of the same face). With the statistical analysis we want to identify spatio-temporal regions with a significant effect of the face type on the ERP, as well as the effect of the time between the repeated presentations of the same face. Categories have been coded as integer values: 1 (famous), 2 (unknown), 3 (scrambled), and the covariates are continuous values.

Model Design

The first step is to design the model corresponding to the study. This design consists of different steps:

The required paths and some additional information have to be defined

PATH_TO_ROOT  = bids_root_folder;        % location of the top level BIDS directory with the raw data
PATH_TO_DERIV = bids_derivatives_folder; % location of the preprocessed EEG data

% define the case (sensor or source level analysis)
SOURCE_ANALYSIS = false; % set to true if you analyse source data

% define the task to analyse
task_name = 'faceStudy';

% trial start and end
trial_start = -200; % starting time of the trial in ms
trial_end   =  500; % ending time of the trial in ms

We define the contrast we want to study

contrast.mat = [1 -0.5 -0.5]; % contrast between famous (the first value) and other categories (the sum of the 2nd and 3rd value)

The split of the covariates (regressors) has to be defined. Here we want to create 1 column of covariates-by-regressor to analyse the influence on each condition:

regress_cat = { 1 , 1;
                2 , 2;
                3 , 3};  % correspondance between covariate and categories. Here, we create 1 column of covariate by category.

% Note: the following syntax has to be respected for the mapping (/!\ don't use the value 0 /!\):
% { first_regressor_merging,  corresponding_value;
%   second_regressor_merging, corresponding_value;
%   nth_regressor_merging,    corresponding_value    }

In case there are several covariates, we select the desired covariates (regressors) to study. Here there is only one covariate

my_trialinfo = 'trialinfo.mat'; % information about trials for each subject, as defined by FT_DEFINETRIAL and FT_PREPROCESSING
selected_regressors = 4;        % selection from trialinfo.Properties.VariableNames (here, the first 3 columns correspond to the categories and the 4th one is the covariate)

Create the model. This calls raw data of each subject and designs the required matrices and can take a few minutes.

model = create_model(PATH_TO_DERIV, PATH_TO_SOURCE, SOURCE_ANALYSIS, task_name, my_trialinfo, trial_start, trial_end, selected_regressors, regress_cat);

First level analysis

The beta and contrast estimates are computed subject-by-subject through a parallel computing pipeline. As we want both the betas (i.e. the ERP model) and contrast (the conditional difference) to be computed and stored as “derivatives 2” (cf. the pipeline figure above), we do the following:

cd(PATH_TO_DERIV)
option = 'both';    % 'model specification', 'contrast only' or 'both'

Now that everything is properly defined, we can run the computation (Almost all your CPU cores will be requested for this task, it’s time to grab a coffee…)

[LIMO_files, procstatus] = limo_batch(option, model, contrast); % this writes beta and contrast estimates to disk in derivatives 2 folder

Second level analysis

The group-level analysis will run as a parallel computing pipeline on contrast estimates (in this example).

We first need an estimate of the channel locations representing all the subjects. Here we consider the channel-by-channel average position:

expected_chanlocs = limo_avg_expected_chanlocs(PATH_TO_DERIV, model.defaults);

We then select the targeted first-level estimates (here the first contrast, corresponding to face type comparison) and the name of the corresponding statistical test we want to perform

my_con = 'con_1'
cd('derivatives/eeg') %path to 1st level analysis output
LIMOfiles = fullfile(pwd,sprintf('%s_files_GLM_OLS_Time_Channels.txt', my_con));
if ~exist(['derivatives/t_test_' my_con],'dir')
    mkdir(['derivatives/t_test_' my_con])
end
cd(['derivatives/t_test_' my_con])

Finally, we run the second level analysis specifying the desired statistical test, the desired number of bootstrap repetitions, and specifying whether a threshold free cluster enhancement (TFCE, Pernet et al., 2015) has to be computed. Another parallel computing pipeline will start which will not take much time.

stat_test = 'one sample t-test';  % desired statistical test
nboot = 1000;                     % number of boostrap repetition
tfce = true;                      % set this to false if TFCE does not have to be run

LIMOPath = limo_random_select(stat_test,expected_chanlocs,'LIMOfiles',...
    LIMOfiles,'analysis_type','Full scalp analysis',...
    'type','Channels','nboot',nboot,'tfce',tfce,'skip design check','yes');

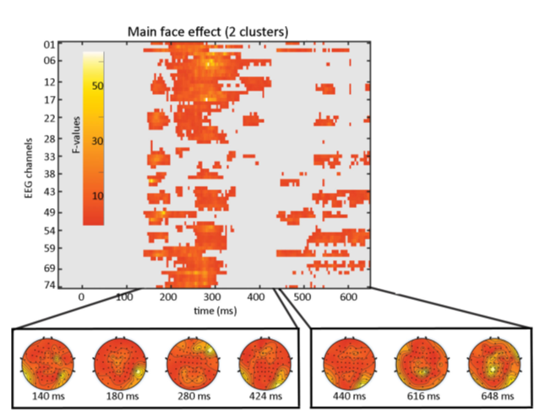
The results can be plotted by calling the limo_results function. By selecting “clustering” as correction for multiple comparisons and the generated “one_sample_ttest_parameter_1.mat” through “image all”, you obtain the regions of significant difference between the categories as shown by this figure: