Whole brain connectivity and network analysis

Introduction

This tutorial will replicate the networkanalysis yet using EEG data instead of MEG. It will demonstrate one of the possible ways to analyze EEG data from a graph theoretical perspective. It is assumed that you are familiar with the various preprocessing steps which will be performed here, as these are not explained further in detail. An overview and detailed information on preprocessing can be found here and on time-frequency analysis here

This tutorial will use metrics that are derived from graph theory and are implemented in the Brain Connectivity Toolbox (BCT, detailed explanation can be found here).

Background

We will analyze brain signals acquired during an Odd-ball task. This data has been previously used in this tutorial. For the purpose of this tutorial will we treat the data as if it was a continuous resting state recording. In contrast to an event-related analysis, where the data is segmented around some external events, we will analyze the entire continuous recording. We will compute connectomes that quantify the ‘connectivity’ between all pairs of pre defined regions, adopting a parcellation approach.

Such connectomes are typically used for a subsequent graph analysis, to extract specific structure in the connections. We will illustrate this by visualizing the node degree.

Also, we will explore the connectomes in more detail, and investigate how the spatial structure changes when moving from one seed location to another.

Procedure

The data analyses will follow the following steps:

• Load the data into MATLAB select the EEG electrodes using ft_selectdata and convert the units of the electrodes from cm to mm using ft_convert_units.
• Cut the data into overlapping segments with ft_redefinetrial.
• Compute sensor level power spectra and determine peak frequency using ft_freqanalysis and ft_multiplotER.
• Align the EEG electrodes to the scalp surface using ft_electroderealign.
• Plot and evaluate the alignment using ft_plot_headmodel, ft_plot_mesh and ft_plot_sens in combination.
• Construct a forward model using ft_prepare_leadfield.
• Compute spatial filters and estimate the amplitude of the sources using ft_sourceanalysis.
• Visualize the results, with ft_sourceplot.
• Compute “all-to-all” connectivity between dipole locations using ft_connectivityanalysis.
• Reduce the size of the connectivity matrix using a parcellation-approach, with ft_sourceparcellate.
• Compute “node degree” using ft_networkanalysis.
• Visualize the results, with ft_sourceplot.

Preprocessing

Reading the data

The aim is to identify the frequency and topography of an 10Hz oscillation. You can download the required data from https://download.fieldtriptoolbox.org/tutorial/networkanalysis_eeg/. This latter folder contains a few files that we will need later in this tutorial as well, so it is recommended to download its contents.

%% load EEG data
load('data_eeg_reref_ica.mat')
load('elec.mat')
% select EEG electrodes only
cfg         = [];
cfg.channel = elec.label;
data        = ft_selectdata(cfg,data_eeg_reref_ica);
data        = rmfield(data,'grad');
% convert elec positions in mm
elec        = ft_convert_units(elec,'mm');
data.elec   = elec;

Prepare electrode layout for plotting

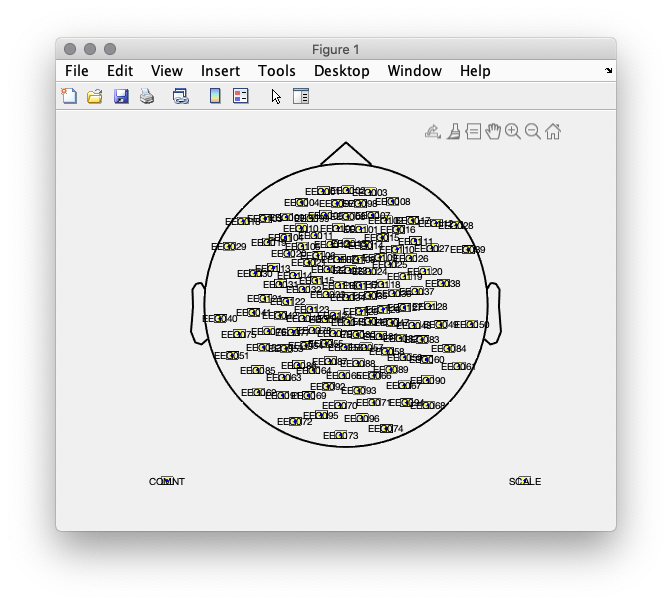
Using the EEG electrodes we compute a 2D layout in order to plot topographies. We use ft_prepare_layout and visualize it using ft_plot_layout.

%% prepare layout and plot
cfg         = [];
cfg.elec    = elec;
layout      = ft_prepare_layout(cfg);
%% scale the layout to fit the head outline
lay         =layout;
lay.pos     =layout.pos./.7;
lay.pos(:,1)=layout.pos(:,1)./.9;
lay.pos(:,2)=layout.pos(:,2)+.08;
lay.pos(:,2)=lay.pos(:,2)./.7;
figure(1);
ft_plot_layout(lay)

Figure 1: 2D electrode layout.

Data segmentation

Next, the data is segmented into overlapping segments of 1 second length.

%% resegment the data into 1 sec chunks
cfg         = [];
cfg.length  = 1;
cfg.overlap = .5;
dataseg     = ft_redefinetrial(cfg,data);

Spectral analysis and peak picking

We will analyze the spectral content of the data using ft_freqanalysis and subsequently interactively explore the data with ft_topoplotER and ft_singleplotER. For those interested in more detailed overview of the configuration options and strategies please refer to our video lectures here and also here.

%% compute the power spectrum
cfg              = [];
cfg.output       = 'pow';
cfg.method       = 'mtmfft';
cfg.taper        = 'hanning';
cfg.keeptrials   = 'no';
datapow          = ft_freqanalysis(cfg, dataseg);
%% plot the topography and the spectrum
figure(1);

cfg             = [];
cfg.layout      = lay;
cfg.xlim        = [9 11];
subplot(1,2,1); ft_topoplotER(cfg, datapow);

cfg             = [];
cfg.channel     = {'EEG087', 'EEG088'};
cfg.xlim        = [3 30];
subplot(1,2,2); ft_singleplotER(cfg, datapow);

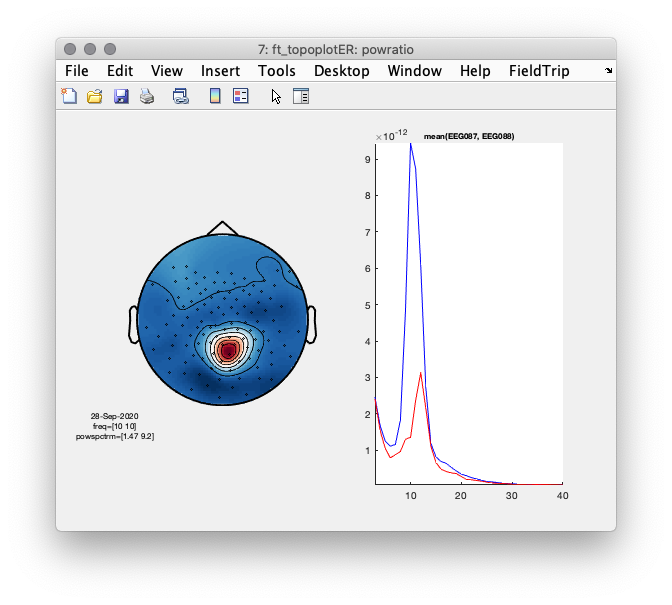
Figure 2: Left- scalp topography of oscillatory power centered at 10 Hz. Right- power spectrum averaged over two occipital sensors illustrating a clear ~10 Hz peak.

Computation of the forward model

We first load the precomputed mni-standard Desikan-Killiani atlas, BEM headmodel and the sourcemodel. In the following section we will compute the forward model, i.e. the leadfield matrix that defines for a set of predefined dipole locations the expected electromagnetic scalp distribution as it is picked up by the EEG electrodes. In this tutorial we will use a cortical sheet based source model, in which the individual dipole locations are constrained to the cortical sheet. This anatomical model has been obtained with freesurfer and it takes quite some time to generate. This falls outside the scope of this tutorial. If you would like to get an idea how this can be done, please have a look at our sourcemodel tutorial. Alternatively, one could create a volumetric dipole grid based on regularly spaced 3-dimensional grid of dipole locations, or an inverse-warp from MNI normalized volumetric space of a template 3D grid. More information about this can be found in our sourcemodel tutorial as well.

%% load the required geometrical information
load('dkatlas.mat')
load('headmodel_eeg.mat')
load('sourcemodel.mat')
%% visualize the coregistration of sensors, headmodel, and sourcemodel.
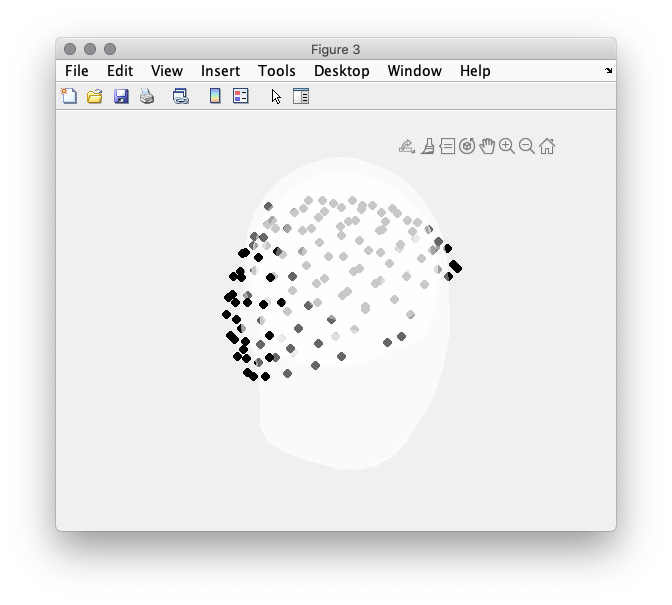
figure(3);
% make the headmodel surface transparent
ft_plot_headmodel(headmodel_eeg, 'edgecolor', 'none'); alpha 0.4
ft_plot_sens(dataseg.elec);
view([45 -15 0])

Figure 3: Misalignment between headmodel and electrode array.

In Figure 3 it is apparent that the electrodes do not align with the scalp surface. To achieve this we use ft_electroderealign in an interactive mode. Figure 4 provides the settings that had been used to align the electrodes. In particular, the option rotate, scale and translate in Figure 3. %% cfg = []; cfg.method = ‘interactive’; cfg.headshape = headmodel_eeg.bnd(1); cfg.elec = elec; elec_aligned = ft_electroderealign(cfg); % make sure the aligned electrodes are updated dataseg.elec = elec_aligned;

Figure 4: Headmodel and electrode array aligned correctly.

Before we proceed it is always useful to check the coregistration between the electrodes, headmodel and sourcemodel.

%% visualize the coregistration of electrodes, headmodel, and sourcemodel.
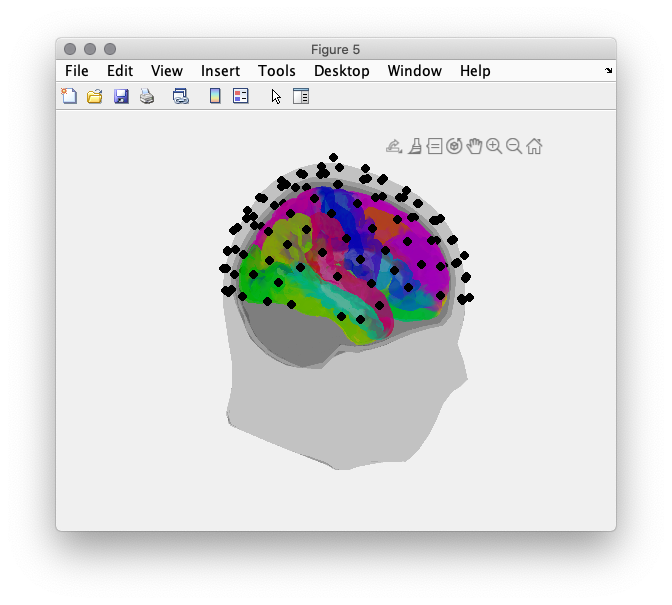
figure(5);

% create colormap to plot parcels in different color
nLabels     = length(dkatlas.tissuelabel);
colr        = hsv(nLabels);
vertexcolor = ones(size(dkatlas.pos,1), 3);
for i = 1:length(dkatlas.tissuelabel)
    index = find(dkatlas.tissue==i);
   if ~isempty(index)
      vertexcolor(index,:) = repmat(colr(i,:),  length(index), 1);
   end
end

% make the headmodel surface transparent
ft_plot_headmodel(headmodel_eeg, 'edgecolor', 'none','facecolor', 'black'); alpha 0.1
ft_plot_mesh(dkatlas, 'facecolor', 'brain',  'vertexcolor', vertexcolor, 'facealpha', .5);
ft_plot_sens(elec_aligned);
view([0 -90 0])

Figure 5: Alignment of headmodel (grey), electrodes (black) and sourcemodel(color). Individual parcels are assigned different color value.

Now we can proceed with the computation of the leadfield matrix, using ft_prepare_leadfield.

cfg         = [];
cfg.elec    = elec_aligned;
cfg.channel = dataseg.label;
cfg.sourcemodel.pos    = sourcemodel.pos;           % 2002v source points
cfg.sourcemodel.inside = 1:size(sourcemodel.pos,1); % all source points are inside of the brain
cfg.headmodel = headmodel_eeg;                      % volume conduction model
leadfield     = ft_prepare_leadfield(cfg);

Source reconstruction and comparison of trials with high and low alpha power

In addition to a forward model, the beamformer needs a sensor-level covariance matrix, or a cross-spectral density matrix. The preliminaries for the cross-spectral density matrix can be obtained with

ft_freqanalysis. In this tutorial, you will compute a memory-wise more compact representation of the single epoch spectral representation, from which the cross-spectral density can be computed in a straightforward way. This will be done ‘under the hood’ in ft_sourceanalysis, so you don’t need to worry about this particular conversion step.

%% compute sensor level Fourier spectra, to be used for cross-spectral density computation.
cfg            = [];
cfg.method     = 'mtmfft';
cfg.output     = 'fourier';
cfg.keeptrials = 'yes';
cfg.tapsmofrq  = 1;
cfg.foi        = 10;
freq           = ft_freqanalysis(cfg, dataseg);

Next, we call ft_sourceanalysis with ‘pcc’ as method. Essentially, this methods implements DICS (the underlying algorithm for computing the spatial filters is according to DICS), but provides more flexibility with respect to data handling. In this context, the advantage is that the ‘pcc’-implementation directly outputs, for each dipole location in the sourcemodel, the fourier coefficients (i.e. phase and amplitude estimates) for each of the trials. This can subsequently be used in a straightforward way for connectivity analysis. In contrast, using ‘dics’ as a method, to obtain the single trial representation of phase and amplitude is quite a bit more tedious.

%% do the source reconstruction
cfg                   = [];
cfg.frequency         = freq.freq;
cfg.method            = 'pcc';
cfg.sourcemodel       = leadfield;
cfg.headmodel         = headmodel_eeg;
cfg.keeptrials        = 'yes';
cfg.pcc.lambda        = '10%';
cfg.pcc.projectnoise  = 'yes';
cfg.pcc.fixedori      = 'yes';
cfg.elec              = elec_aligned;
source = ft_sourceanalysis(cfg, freq);
source = ft_sourcedescriptives([], source); % to get the neural-activity-index

Visualization of the neural-activity-index

In order to visualize source-reconstructed data, the function ft_sourceplot can be used. If the input data contains the dipole positions defined on a triangulated mesh (i.e. it contains both a ‘pos’ and a ‘tri’ field), one should use the ‘surface’ method.

%% plot the neural activity index (power/noise)

cfg           = [];
cfg.parameter = 'nai';
sourceint     = ft_sourceinterpolate(cfg, source, dkatlas);
sourceint     = ft_sourceparcellate([], sourceint, dkatlas);

cfg               = [];
cfg.method        = 'surface';
cfg.funparameter  = 'nai';
cfg.maskparameter = cfg.funparameter;
cfg.opacitymap    = 'rampup';
cfg.colorbar      = 'no';

figure(6);
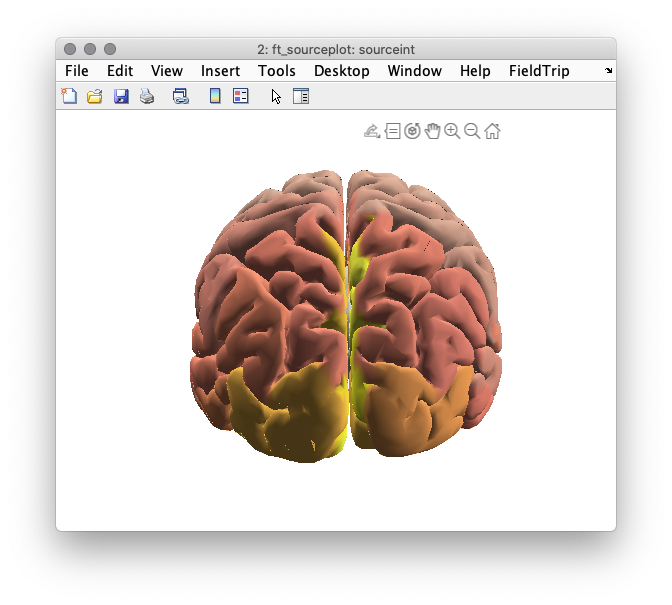
ft_sourceplot(cfg, sourceint);
colorbar off
view([-90 30]);
light('Position',[0,-90 30])
material dull
set(gcf,'color','w');

Figure 6: Reconstructed activity (neural activity index) of resting state alpha power is not as instructive as one would hope.

Creation of a ‘pseudo-contrast’ based on a median split of the epochs

Typically, in an experimental context, it is useful to visualize activity contrasts, e.g., baseline vs. activation intervals, in order to get spatially interpretable beamformer results. Although the neural-activity-index intends to improve interpretability by normalization with a poor man’s approximation of the projected noise, and although it takes care of the depth bias of the beamformer to some extent, it doesn’t usually work well. In order to convince ourselves that the beamformer is adequately reconstructing the activity of the neural sources, we will resort here to faking an ‘experimental’ contrast, using a median split of the data, where the data are split according to occipital alpha power. This requires an estimate of the single epoch alpha power. Next, identify the epoch indices for which the alpha power is less/more than the median across epochs.

%% compute sensor level single trial power spectra
cfg              = [];
cfg.output       = 'pow';
cfg.method       = 'mtmfft';
cfg.taper        = 'hanning';
cfg.foilim       = [9 11];
cfg.tapsmofrq    = 1;
cfg.keeptrials   = 'yes';
datapow          = ft_freqanalysis(cfg, dataseg);
cfg.foilim       = [3 40];
datapowfull      = ft_freqanalysis(cfg, dataseg);

%% identify the indices of trials with high and low alpha power
freqind = nearest(datapow.freq, 10);
tmp     = datapow.powspctrm(:,:,freqind);
chanind = find(mean(tmp,1)==max(mean(tmp,1)));  % find the sensor where power is max
indlow  = find(tmp(:,chanind)<=median(tmp(:,chanind)));
indhigh = find(tmp(:,chanind)>=median(tmp(:,chanind)));

Now, we can compute the spectra for the two sets of epochs using ft_freqdescriptives and compute the difference with ft_math

%% compute the power spectrum for the median splitted data
cfg              = [];
cfg.trials       = indlow;
datapow_low      = ft_freqdescriptives(cfg, datapowfull);

cfg.trials       = indhigh;
datapow_high     = ft_freqdescriptives(cfg, datapowfull);

%% compute the difference between high and low
cfg = [];
cfg.parameter = 'powspctrm';
cfg.operation = 'divide';
powratio      = ft_math(cfg, datapow_high, datapow_low);

%% plot the topography of the difference along with the spectra
cfg        = [];
cfg.layout = lay;
cfg.xlim   = [9.9 10.1];
figure(7);
subplot(1,2,1);ft_topoplotER(cfg, powratio);

cfg         = [];
cfg.channel = {'EEG087', 'EEG088'};
subplot(1,2,2);ft_singleplotER(cfg, datapow_high, datapow_low);

Figure 7: Difference topography (left) and power spectra of the median splitted data, according to 10 Hz power at sensor ‘EEG087’.

Source reconstruction of ‘low’ and ‘high’ alpha activity epochs

Now we will compute the source reconstructed alpha power again, as illustrated above, based on the median split. We will use a common filter approach, where we compute the spatial filters based on the cross-spectral density averaged across all epochs. See also here and here for further information on common filters.

%% compute fourier spectra for frequency of interest according to the trial split
cfg            = [];
cfg.method     = 'mtmfft';
cfg.output     = 'fourier';
cfg.keeptrials = 'yes';
cfg.tapsmofrq  = 1;
cfg.foi        = 10;

cfg.trials = indlow;
freq_low   = ft_freqanalysis(cfg, dataseg);

cfg.trials = indhigh;
freq_high  = ft_freqanalysis(cfg, dataseg);

%% compute the beamformer filters based on the entire data
cfg                   = [];
cfg.frequency         = freq.freq;
cfg.method            = 'pcc';
cfg.sourcemodel       = leadfield;
cfg.headmodel         = headmodel_eeg;
cfg.elec              = elec_aligned;
cfg.keeptrials        = 'yes';
cfg.pcc.lambda        = '10%';
cfg.pcc.projectnoise  = 'yes';
cfg.pcc.keepfilter    = 'yes';
cfg.pcc.fixedori      = 'yes';
source = ft_sourceanalysis(cfg, freq);

% use the precomputed filters
cfg                   = [];
cfg.frequency         = freq.freq;
cfg.method            = 'pcc';
cfg.sourcemodel       = leadfield;
cfg.sourcemodel.filter = source.avg.filter;
cfg.headmodel         = headmodel_eeg;
cfg.elec              = elec_aligned;
cfg.keeptrials        = 'yes';
cfg.pcc.lambda        = '10%';
cfg.pcc.projectnoise  = 'yes';
source_low  = ft_sourcedescriptives([], ft_sourceanalysis(cfg, freq_low));
source_high = ft_sourcedescriptives([], ft_sourceanalysis(cfg, freq_high));

cfg           = [];
cfg.operation = 'log10(x1)-log10(x2)';
cfg.parameter = 'pow';
source_ratio  = ft_math(cfg, source_high, source_low);

We now visualize the log-difference on the cortical sheet.

cfg           = [];
cfg.parameter = 'pow';
sourceint     = ft_sourceinterpolate(cfg, source_ratio, dkatlas);
sourceint     = ft_sourceparcellate([], sourceint, dkatlas);

cfg              = [];
cfg.method       = 'surface';
cfg.funparameter = 'pow';
cfg.colorbar     = 'no';
cfg.funcolormap  = '*RdBu';
figure(8);ft_sourceplot(cfg, sourceint);
view([-90 30]);
light('style','infinite','position',[0 -200 200]);
colorbar off
material dull
set(gcf,'color','w');

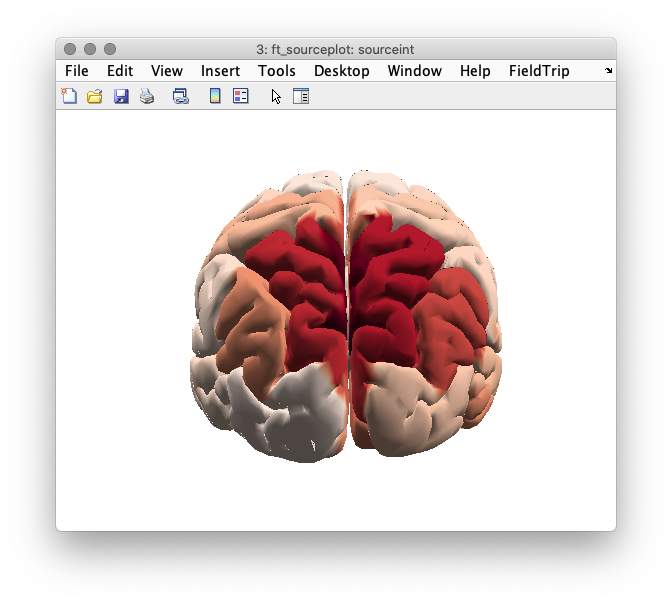
Figure 8: Source reconstructed activity illustrating the relative difference in alpha power between the high and low alpha conditions.

Connectivity analysis and parcellation

Computation of connectivity

Next, we will call ft_connectivityanalysis to compute a connectivity matrix between all pairs of dipoles, which is sometimes referred to as a ‘connectome’. There are several connectivity measures to choose from. Here, we first will compute the imaginary part of the coherencey, using cfg.method = ‘coh’; and cfg.complex = ‘absimag’;. This syntax will return only the imaginary part of the coherence spectrum and effectivly suppress spurious coherence driven by electromagnetic field spread (Nolte et al. Identifying true brain interaction from EEG data using the imaginary part of coherence. Clinical Neurophysiology, 2004; 115; 2292-2307). For the computation, we take advantage of the fact that the ‘source’ variable constructed earlier, contains the single trial estimates of amplitude and phase at the source-level. This is the consequence of the fact that we used cfg.method=’pcc’ for ft_sourceanalysis, and requested cfg.output = ‘fourier’ for ft_freqanalysis.

%% compute connectivity
cfg         = [];
cfg.method  ='coh';
cfg.complex = 'absimag';
source_conn = ft_connectivityanalysis(cfg, source);

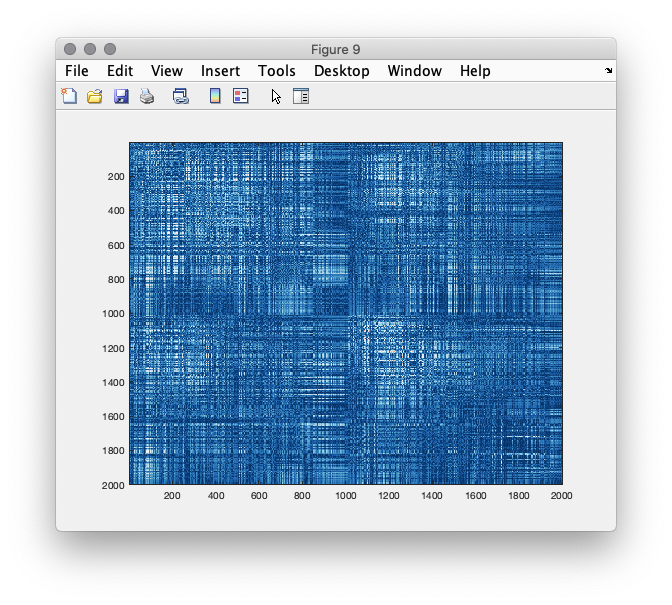
We can now make a, rather uninformative, visualization of the connectome, plotting the full weighted graph, between all pairs of nodes.

figure(9);imagesc(source_conn.cohspctrm);

Figure 9: connectivity matrix between all pairs of dipole locations

Parcellation and network analysis

We can now explore the structure in the estimated connectivity matrices using graph theoretic tools. It is not really clear what the effect of the residual spatial leakage of activity is on the estimates of some of these measures, so we would caution for careful interpretations of graph metrics derived from such connectivity matrices, particularly when comparing groups of experimental participants or experimental conditions. Yet, the intention of this tutorial is still to illustrate how such graph theoretic measures can in principle be computed and visualized using fieldtrip. To this end, we are going to use ft_networkanalysis, using cfg.method = ‘degrees’. Specifying a prior threshold (e.g., cfg.threshold = .1) results in an estimate of the ‘node degree’, i.e. the amount of nodes with which a particular node has an estimated connectivity of (in this case) 0.1 or higher. There are several ways to determine the threshold, for instance based on some statistical parameterization or previous observation in the literature, yet all of them are and remain arbitrary.

cfg           = [];
cfg.method    = 'degrees';
cfg.parameter = 'cohspctrm';
cfg.threshold = .1;
network_full  = ft_networkanalysis(cfg,source_conn);
%% sourceinterpolate
cfg           = [];
cfg.parameter = 'degrees';
network_int   = ft_sourceinterpolate(cfg, network_full, dkatlas);
network_int   = ft_sourceparcellate([], network_int, dkatlas);

%% create a fancy mask
cfg              = [];
cfg.method       = 'surface';
cfg.funparameter = 'degrees';
cfg.colorbar     = 'no';
figure(10);ft_sourceplot(cfg, network_int);
view([-90 30]);
light('style','infinite','position',[0 -200 200]);
colorbar off
material dull
set(gcf,'color','w');

Figure 10: Node degree based on imaginary part of coherency, thresholded at a value of 0.1. Dark colors indicated few suptrathreshold connections, hot colors indicate many suprathreshold connections.

Effect of occipital alpha power on the connectivity results

Using other connectivity metrics

Obviously, one can choose from a large amount of different connectivity measures, each of which has its advantages and disadvantages.