Extracting the brain state and events from continuous sleep EEG
Introduction
In this tutorial you will explore and combine continuous EEG with multiple recordings from other modalities, such as muscles (EMG), eyes (EOG) and the heart (ECG). You will learn how combining the modalities can give a better understanding of the brain states and the switching between them.
We will be using sleep recordings as an example for multimodal data and will form a picture of what is happening in the brain during sleep. Sleep is the most standardized and well-analyzed brain state to date. The methods used for analyzing sleep might also help you in characterizing drowsiness during a task, detect closed eyes or eye movements, detect spontaneous events in EEG (such as epileptic spikes) and in general how to include other modalities relevant to your task. Along the way you will learn a bit about the structure of sleep.
This tutorial assumes that the steps of preprocessing are already clear for the reader.
Background
Multi-modal sleep recordings
Discrete events and continuous shifts in activity during sleep are not easily observed in one modality by itself. They have to be identified and marked by using the combination of the different modalities. This is why sleep recordings span multiple modalities, each with clearly defined changes in the activity that are relatively easy to predict. We have some good understanding about the physiological relationships between the events and what is happening to the different body parts during sleep. Finally, most of the activity which we usually consider as artifacts in our task-related EEG recordings (e.g., eye movements, muscle and heart activity) occur here in a systematic manner and are considered important features of a sleep state rather than an artifact. Thus using sleep data allows us to safely explore how to identify changes in brain state in a well studied example. Here we can gain some skills to explore cross-modality relations in recordings that are less well defined, e.g., task or resting state recordings, or parallel recordings that expand the interpretability by adding features of other or related modalities (e.g., motion sensors, MEG, fMRI).
Sleep states by Polysomnography
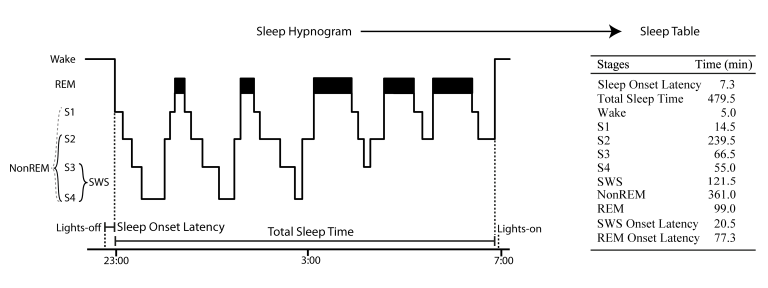
Sleep has well defined brain states which are called Wake, Stage 1, Stage 2, Stage 3, Stage 4 and rapid-eye-movement (REM) sleep. In the more recent terminology Stage 3 and Stage 4 are combined as one stage and called slow-wave sleep (SWS). A more coarse classification consists of Wake, REM and non-REM, where non-REM combines Stage 1, Stage 2 and SWS sleep. Often we have movement arousals as well as longer times with movement during sleep. These arousals and movement times do not necessarily reflect the Wake state, but give us information about sleep as well. Furthermore, the movements indicate where we can find artifactual data in our recordings we might want to exclude for more focused analyses. Sleep states happen usually in clearly defined temporal cycles about every 1 to 2 hours. An idealized sleep “hypnogram” example is given below. However, sleep varies a lot between individuals and real sleep “hypnograms” from two different individuals by expert scoring are given below.
Sleep states can only be reliably identified by using combined EEG, EOG and EMG. But also additional modalities are often recorded, such as ECG, breathing, accelerometers, body temperature, snoring noise etc. This kind of recording of multiple signals during sleep is called polysomnography. Polysomnography is typically scored (i.e. classified) in 30-second segments using a manual procedure.
Figure 1: Hypnogram and sleep stages according to manual sleep scoring rules by Rechtschaffen and Kales (1968) and how they transfer to a sleep table.
The dataset used in this tutorial
For this tutorial we will use recordings from the healthy sample of the CAP Sleep Database that are openly available in PhysioNet (https://www.physionet.org/physiobank/database/capslpdb/). The number of channels has been reduced and the data has been sampled down to 128 Hz for convenience. The data is stored in EDF format and two subjects can be downloaded from our download server.
The EEG channels are called “C4-A1” and “C3-A2”, according to derivations based on the 10-20 system system. These correspond to the potential at C4 referenced to A1 (behind the left ear) and the same for C3 and the right ear. The EOG channel is called “ROC-LOC” for a bipolar derivation between electrodes on the right and left of the eyes. The EMG is “EMG1-EMG2” for a bipolar derivation between two electrodes on the muscles of the chin. The ECG channel is called “ECG1-ECG2”. In the original data already all channels were notch filtered at 50 Hz and the EEG, ECG and EOG was filtered with a high-pass of 0.3 Hz and a low-pass of 30 Hz; the EMG with was already high-pass filtered at 10 Hz and low-pass filtered at 100 Hz.
Procedure
To explore the sleep data, we will perform the following step
- Read the sleep data with ft_preprocessing and view the raw signals in 30-second epochs using ft_databrowser.
- Detect artifactual Wake epochs using ft_artifact_muscle by looking at the EMG and EOG excluding artifactual periods and periods with eye activity from further planned analysis using ft_rejectartifact.
- Estimating the sleep frequencies represented over the course of sleep using ft_freqanalysis and visualize using ft_singleplotTFR and ft_databrowser.
- Identify the sleep state of non-REM by thresholding and combining signals using ft_apply_montage and reading in pre-scored hypnograms for a comparison with the here estimated sleep stages ft_databrowser.
- Find spontaneous ECG events like R-waves and determine the heart rate using ft_artifact_zvalue.
- Find sleep EEG events like slow waves and sleep spindles in the non-REM signal that was cleaned from artifacts using ft_artifact_zvalue, ft_preprocessing, ft_redefinetrial and visualize their time-locked average signals and time-locked frequency activity (ERF) using ft_timelockanalysis, ft_singleplotER, ft_freqanalysis and ft_singleplotTFR and then view them in the browser ft_databrowser.
Preprocessing
The ft_preprocessing function requires the modified sleep datasets and Subject loading code (e.g., Subject05.m), which is available from our download server.
Load the subject specific information. Then read and preprocess the continuous sleep data
% set the path to the data to the current directory
datapath = pwd;
% load the Subject specific information
%Subject01
Subject05
% load the continuous sleep EEG, EOG, EMG and ECG data
cfg = [];
cfg.dataset = [datapath filesep subjectdata.subjectdir filesep subjectdata.datafile];
cfg.continuous = 'yes';
data_orig = ft_preprocessing(cfg);
The provided example data sets were already originally pre-filtered for scoring thus there is no need to filter them again, but they still retain all artifacts.
The data from Subject01 should have the following structure:
data_orig =
hdr: [1x1 struct]
label: {4x1 cell}
time: {[1x4024448 double]}
trial: {[4x4024448 double]}
fsample: 128
sampleinfo: [1 4024448]
cfg: [1x1 struct]
Because the original channels are not named conveniently we apply a montage structure to rename the channel labels to EEG, EOG, EMG and ECG. The montage consists of a matrix of correspondences that changes the original labels by the new ones. By using ft_preprocessing, with this matrix as a part of the cfg option montage, channel labels can be modified.
montage_rename = [];
montage_rename.labelold = {'C4-A1' 'ROC-LOC' 'EMG1-EMG2' 'ECG1-ECG2'};
montage_rename.labelnew = {'EEG' 'EOG' 'EMG' 'ECG'};
montage_rename.tra = eye(4);
cfg = [];
cfg.montage = montage_rename;
data_continuous = ft_preprocessing(cfg, data_orig);
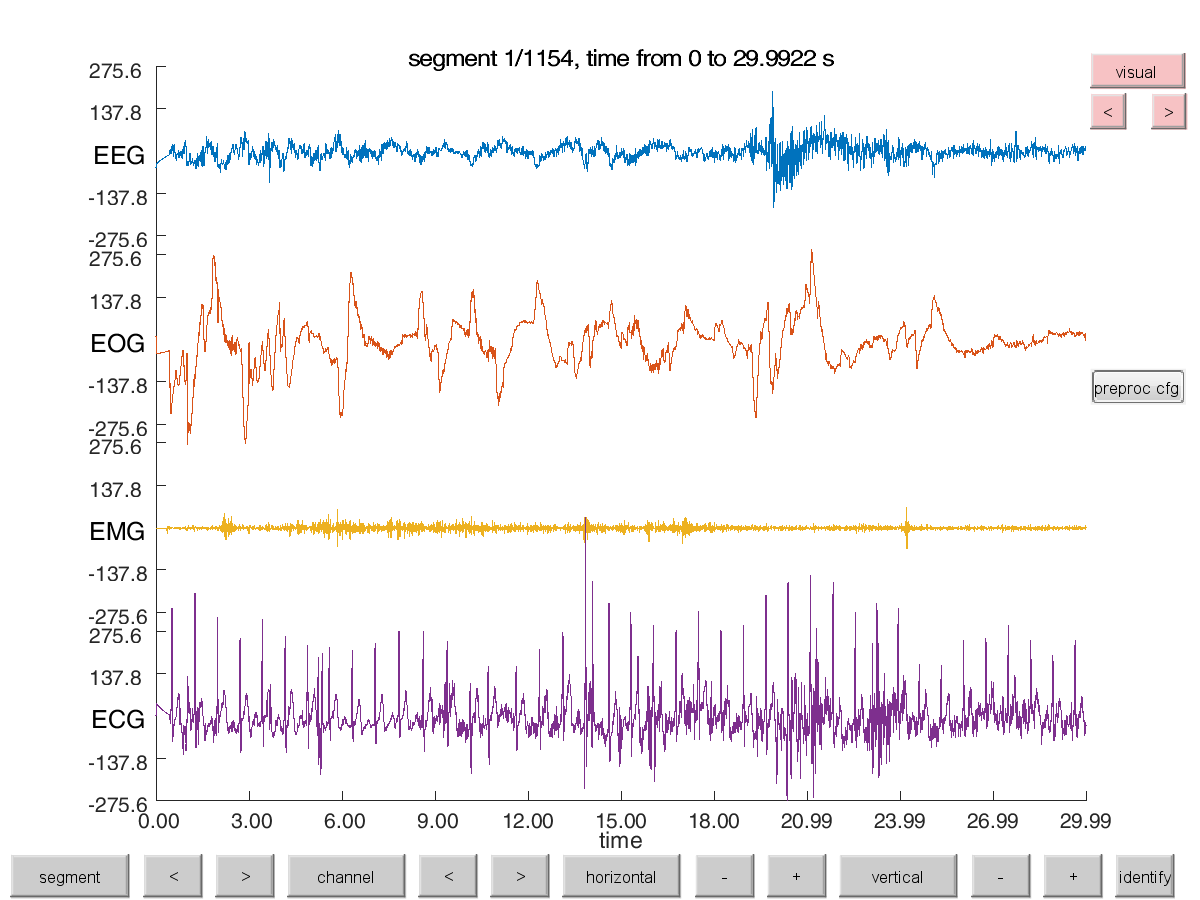
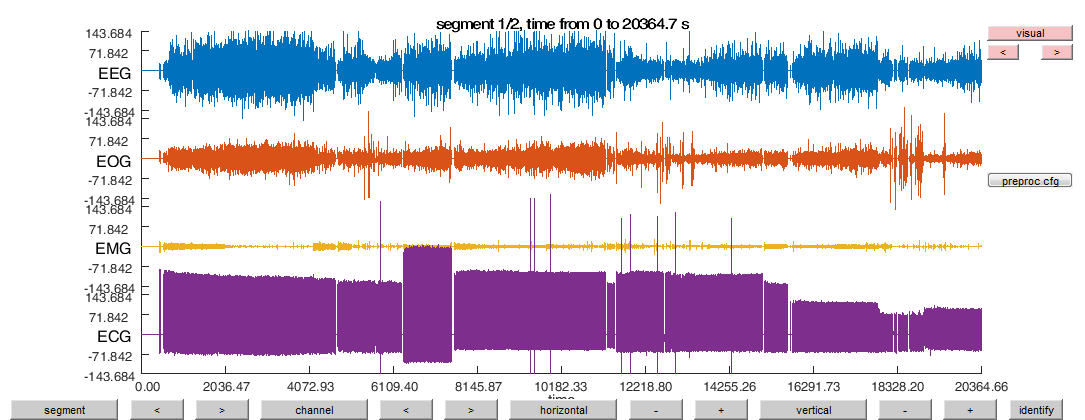
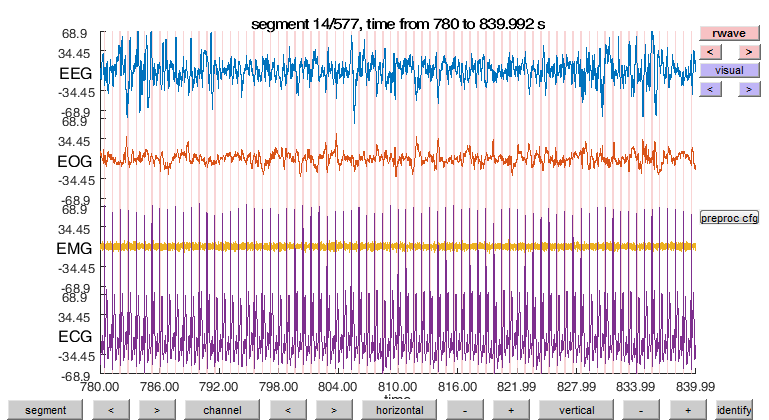
Lets browse the continuous sleep data as typical for sleep scoring in 30-s epochs using ft_databrowser.
Please also skip through several epochs in the data and zoom out in the time axis to view the full data. Play around to get a good feeling for the signals represented and how the different signals look like and change over the time of sleep.
cfg = [];
cfg.continuous = 'yes';
cfg.viewmode = 'vertical'; % all channels separate
cfg.blocksize = 30; % view the continuous data in 30-s blocks
ft_databrowser(cfg, data_continuous);
Figure 2: ft_databrowser of the original data with renamed channels. The data can be horizontally (time axis) and vertically (y-axis/signal amplitude) zoomed in and out to view the data in smaller or larger segments. And data can be viewed segment by segment..
We now additionally segment the continuous data in 30-second trials. This allows us later to perform analyses on the data more efficiently. Also this is the basis to break down the long signal into more comprehensible equal-sized chunks from which we can reconstruct a new signal to better estimate sleep states that clearly switch only on such longer time scales.
% segment the continuous data in segments of 30-seconds
% we call these epochs trials, although they are not time-locked to a particular event
cfg = [];
cfg.length = 30; % in seconds;
cfg.overlap = 0;
data_epoched = ft_redefinetrial(cfg, data_continuous)
Detect wake periods using EMG & EOG
To identify periods of wake (including brief arousals), non-REM and REM states during sleep we use all available modalities of a polysomnogram. We can use information about movement reflected in the level of EMG activity. In order to detect movement artifacts we filter the EMG channel in the 20 to 45 Hz range and apply a Hilbert envelope around the signal and smooth it.
cfg = [];
cfg.continuous = 'yes';
cfg.artfctdef.muscle.interactive = 'yes';
% channel selection, cutoff and padding
cfg.artfctdef.muscle.channel = 'EMG';
cfg.artfctdef.muscle.cutoff = 4; % z-value at which to threshold (default = 4)
cfg.artfctdef.muscle.trlpadding = 0;
% algorithmic parameters
cfg.artfctdef.muscle.bpfilter = 'yes';
cfg.artfctdef.muscle.bpfreq = [20 45]; % typicall [110 140] but sampling rate is too low for that
cfg.artfctdef.muscle.bpfiltord = 4;
cfg.artfctdef.muscle.bpfilttype = 'but';
cfg.artfctdef.muscle.hilbert = 'yes';
cfg.artfctdef.muscle.boxcar = 0.2;
Please note that due to the reduced sample rate of 128 Hz we cannot use the typical frequency range to better detect EMG, however this should suffice for our case.
We now use ft_artifact_muscle for automated artifact rejection according to some threshold (for more information on the active mode of this function see also the automatic artifact rejection tutorial).
We want to be very cautious with excluding and exclude more than we must since EMG artifacts point towards movement or wake periods have happened probably some seconds earlier and later.
% conservative rejection intervals around EMG events
cfg.artfctdef.muscle.pretim = 10; % pre-artifact rejection-interval in seconds
cfg.artfctdef.muscle.psttim = 10; % post-artifact rejection-interval in seconds
% keep a copy for the exercise
cfg_muscle_epoched = cfg;
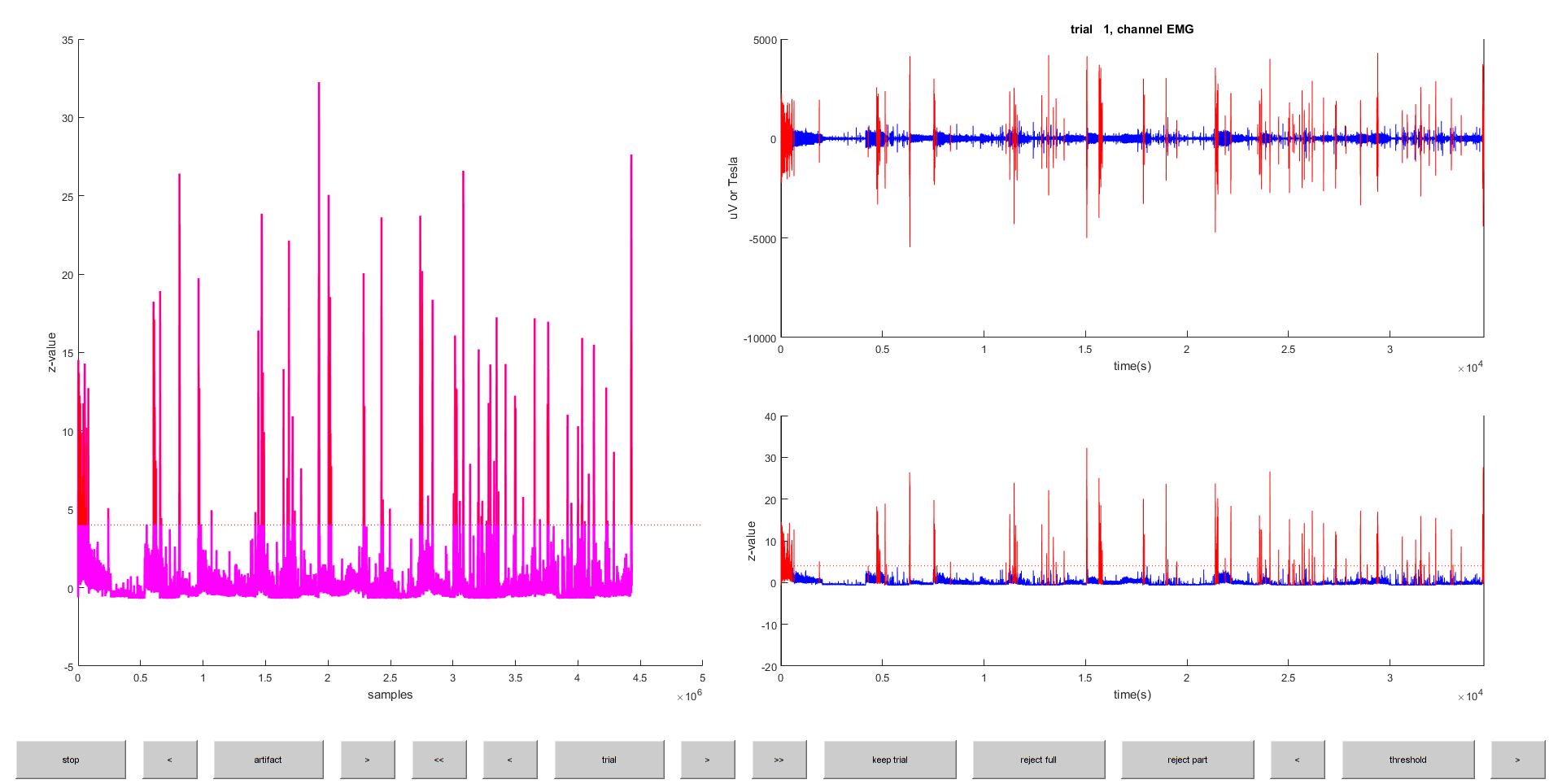
% feedback, explore the right threshold for all data (one trial, th=4 z-values)
cfg = ft_artifact_muscle(cfg, data_continuous);
% make a copy of the samples where the EMG artifacts start and end, this is needed further down
EMG_detected = cfg.artfctdef.muscle.artifact;
Exercise 1
Explore and find the best cutoff in z-values (i.e. standard deviations) to exclude most of the artifacts for this subject!
Typically EMG higher than 100 microVolts are best excluded. Note that we exclude the data on the whole data length, i.e. as one big trial.
Figure 3: Interactive figure of ft_artifact_muscle. The left panel shows the z-score of the processed data. Suprathreshold data points are marked in red. The lower right panel shows one trial, which in our case is the same as on the left panel, as we inspect the data all in one..
We can now look at the detected “artifacts” using ft_databrowser
cfg_art_browse = cfg;
cfg_art_browse.continuous = 'yes';
cfg_art_browse.viewmode = 'vertical';
cfg_art_browse.blocksize = 30*60; % view the data in 10-minute blocks
ft_databrowser(cfg_art_browse, data_continuous);
For the epoched data we can do a similar EMG artifact identification as abov
cfg_muscle_epoched.continuous = 'no';
cfg_muscle_epoched.artfctdef.muscle.interactive = 'yes';
cfg_muscle_epoched = ft_artifact_muscle(cfg_muscle_epoched, data_epoched);
Exercise 2
Compare the artifact begin and end samples when detected in the continuous data and when detected in the epoched data. What do you notice?
Another indicator of wake periods (or REM sleep) is eye movement. In the EOG we observe different types of eye movements (blinks, normal, slow, and rapid eye movements). Therefore, we will next detect periods with increased EO
cfg = [];
cfg.continuous = 'yes';
cfg.artfctdef.eog.interactive = 'yes';
% channel selection, cutoff and padding
cfg.artfctdef.eog.channel = 'EOG';
cfg.artfctdef.eog.cutoff = 2.5; % z-value at which to threshold (default = 4)
cfg.artfctdef.eog.trlpadding = 0;
cfg.artfctdef.eog.boxcar = 10;
% conservative rejection intervals around EOG events
cfg.artfctdef.eog.pretim = 10; % pre-artifact rejection-interval in seconds
cfg.artfctdef.eog.psttim = 10; % post-artifact rejection-interval in seconds
Exercise 3
Explore the right threshold for detecting all EOG artifacts. Again, the data is displayed as one single long trial.
cfg = ft_artifact_eog(cfg, data_continuous);
% make a copy of the samples where the EOG artifacts start and end, this is needed further down
EOG_detected = cfg.artfctdef.eog.artifact;
To exclude these epochs with artifacts from analysis we use ft_rejectartifact and replace all the artifactual data points in all channels of the continuous sleep data with zeros by using the option cfg.artfctdef.reject ‘value’ and setting it to 0.
% replace the artifactual segments with zero
cfg = [];
cfg.artfctdef.muscle.artifact = EMG_detected;
cfg.artfctdef.eog.artifact = EOG_detected;
cfg.artfctdef.reject = 'value';
cfg.artfctdef.value = 0;
data_continuous_clean = ft_rejectartifact(cfg, data_continuous);
data_epoched_clean = ft_rejectartifact(cfg, data_epoched);
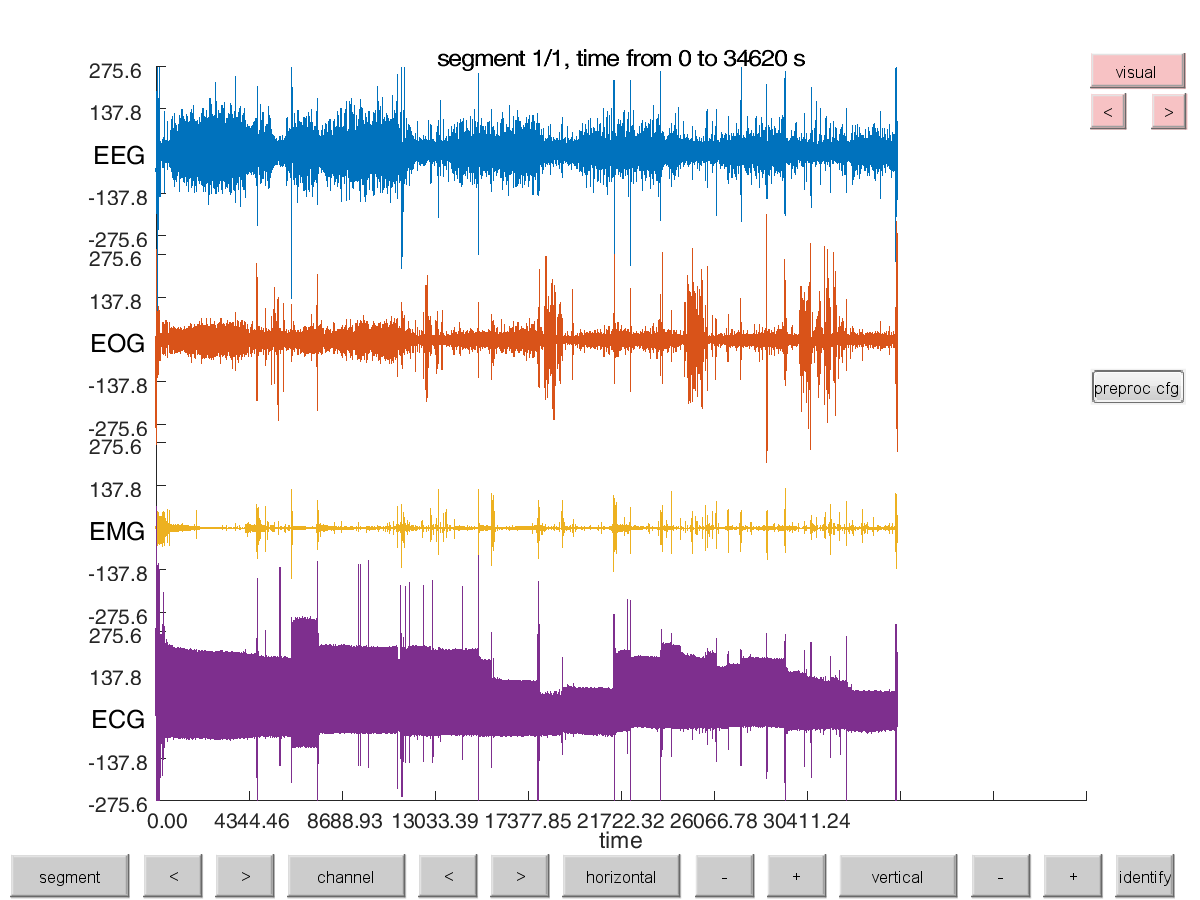
Let us view the data in 2-hour blocks again after excluding the parts with EMG or EOG artifact
cfg = [];
cfg.continuous = 'yes';
cfg.viewmode = 'vertical';
cfg.blocksize = 60*60*2; % view the data in blocks
ft_databrowser(cfg, data_continuous_clean);
Estimating frequency-representation over sleep
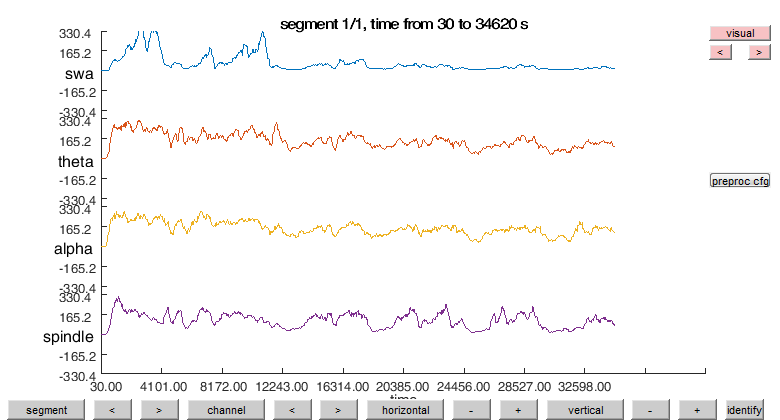
Electrophysiological recordings can also be used to identify wake periods. In the EEG we focus on 4 frequency bands, which are slow-wave activity (0.5 to 4 Hz), theta (4 to 8 Hz), alpha (8-11) and sleep spindle band/ sigma (11-16 Hz). Note that the frequency bands might be defined here differently than in some other literature.
% define the EEG frequency bands of interest
freq_bands = [
0.5 4 % slow-wave band actity
4 8 % theta band actity
8 11 % alpha band actity
11 16 % spindle band actity
];
cfg = [];
cfg.output = 'pow';
cfg.channel = 'EEG';
cfg.method = 'mtmfft';
cfg.taper = 'hanning';
cfg.foi = 0.5:0.5:16; % in 0.5 Hz steps
cfg.keeptrials = 'yes';
freq_epoched = ft_freqanalysis(cfg, data_epoched_clean)
freq_epoched =
label: {'EEG'}
dimord: 'rpt_chan_freq'
freq: [1x32 double]
powspctrm: [1154x1x32 double]
cumsumcnt: [1154x1 double]
cumtapcnt: [1154x1 double]
cfg: [1x1 struct]
Now comes a trick to analyze the data more efficiently: the trials/segments/epochs in the data represent time at the level of the experiment, i.e. every subsequent trial is one 30-s epoch advanced in time. We can reformat the rpt_chan_freq structure into a regular time-frequency representation with chan_freq_time. The time or latency of each trial can be constructed using the sampleinfo from the segmented data, which specified for each trial the begin and the end-sample relative in the original datafile. See also the frequently asked question “how can I do time-frequency analysis on continuous data” for more details.
begsample = data_epoched_clean.sampleinfo(:,1);
endsample = data_epoched_clean.sampleinfo(:,2);
time = ((begsample+endsample)/2) / data_epoched_clean.fsample;
Then we proceed by copying the freq structure, in which we flip the power spectrum to change the “rpt” (that means the trial) dimension into the “time” dimension (that is now the time, as each trial is now considered one datapoint
freq_continuous = freq_epoched;
freq_continuous.powspctrm = permute(freq_epoched.powspctrm, [2, 3, 1]);
freq_continuous.dimord = 'chan_freq_time'; % it used to be 'rpt_chan_freq'
freq_continuous.time = time; % add the description of the time dimension
Now we can view the final time-frequency over the whole night
figure
cfg = [];
cfg.baseline = [min(freq_continuous.time) max(freq_continuous.time)];
cfg.baselinetype = 'normchange';
cfg.zlim = [-0.5 0.5];
ft_singleplotTFR(cfg, freq_continuous);
What we need in the end is time-frequency spectra over specific frequency bands. So for each frequency band we select and average from the previous time-frequency structure computed over a wider range of bands.
cfg = [];
cfg.frequency = freq_bands(1,:);
cfg.avgoverfreq = 'yes';
freq_continuous_swa = ft_selectdata(cfg, freq_continuous);
cfg = [];
cfg.frequency = freq_bands(2,:);
cfg.avgoverfreq = 'yes';
freq_continuous_theta = ft_selectdata(cfg, freq_continuous);
cfg = [];
cfg.frequency = freq_bands(3,:);
cfg.avgoverfreq = 'yes';
freq_continuous_alpha = ft_selectdata(cfg, freq_continuous);
cfg = [];
cfg.frequency = freq_bands(4,:);
cfg.avgoverfreq = 'yes';
freq_continuous_spindle = ft_selectdata(cfg, freq_continuous);
Concatenate the average frequency band signals to one data trial and combine the channels with each one frequency band to a single data structure:
data_continuous_swa = [];
data_continuous_swa.label = {'swa'};
data_continuous_swa.time{1} = freq_continuous_swa.time;
data_continuous_swa.trial{1} = squeeze(freq_continuous_swa.powspctrm)';
data_continuous_swa_spindle = [];
data_continuous_swa_spindle.label = {'theta'};
data_continuous_swa_spindle.time{1} = freq_continuous_theta.time;
data_continuous_swa_spindle.trial{1} = squeeze(freq_continuous_theta.powspctrm)';
data_continuous_alpha = [];
data_continuous_alpha.label = {'alpha'};
data_continuous_alpha.time{1} = freq_continuous_alpha.time;
data_continuous_alpha.trial{1} = squeeze(freq_continuous_alpha.powspctrm)';
data_continuous_spindle = [];
data_continuous_spindle.label = {'spindle'};
data_continuous_spindle.time{1} = freq_continuous_spindle.time;
data_continuous_spindle.trial{1} = squeeze(freq_continuous_spindle.powspctrm)';
cfg = [];
data_continuous_perband = ft_appenddata(cfg, ...
data_continuous_swa, ...
data_continuous_swa_spindle, ...
data_continuous_alpha, ...
data_continuous_spindle);
The resulting data structure should then look like this:
data_continuous_perband =
label: {4x1 cell}
trial: {[4x1154 double]}
time: {[1x1154 double]}
cfg: [1x1 struct]
Now we divide the signal by its standard deviation and scale it with a factor of 100 to make changes in the signal equally visible across frequency bands, because usually each frequency band has different absolute power values (higher frequency usually means less absolute power in brain signals).
cfg = [];
cfg.scale = 100; % in percent
cfg.demean = 'no';
data_continuous_perband = ft_channelnormalise(cfg, data_continuous_perband);
Apply a smoothing filter with a 300-second boxcar
cfg = [];
cfg.boxcar = 300;
data_continuous_perband = ft_preprocessing(cfg, data_continuous_perband);
View the whole sleep data in frequency band power
cfg = [];
cfg.continuous = 'yes';
cfg.viewmode = 'vertical';
cfg.blocksize = 60*60*2; %view the whole data in blocks
ft_databrowser(cfg, data_continuous_perband);
Identify non-REM sleep
We will now focus on non-REM EEG activity. This will help us to better identify non-REM events within the data by ignoring Wake and REM and artifactual epochs. We take use of the previous information about artifactual epochs we identified with EMG and epochs free of EOG activity (that are typical for Wake or REM sleep).
Create a new combined channel from the normalized signal of slow-wave activity (SWA) and spindle. This helps us to better find the epochs that are either high in spindles or have a lot of slow waves (which is typical for non-REM sleep).
montage_sum = [];
montage_sum.labelold = {'swa', 'theta', 'alpha', 'spindle'};
montage_sum.labelnew = {'swa', 'theta', 'alpha', 'spindle', 'swa+spindle'};
montage_sum.tra = [
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
1 0 0 1 % the sum of two channels
];
cfg = [];
cfg.montage = montage_sum;
data_continuous_perband_sum = ft_preprocessing(cfg, data_continuous_perband);
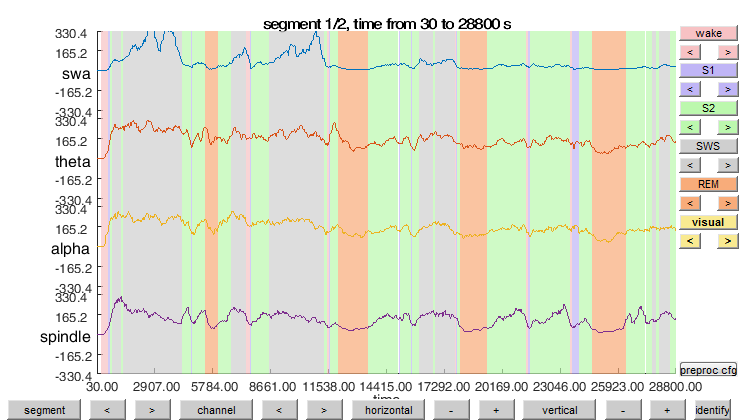
View the whole sleep data in frequency band power now including the combined sleep spindle and SWA power. Is this enough t to find the sleep stages and cycles?
cfg = [];
cfg.continuous = 'yes';
cfg.viewmode = 'vertical';
cfg.blocksize = 60*60*2; % view the whole data in blocks
ft_databrowser(cfg, data_continuous_perband_sum);
As an estimate to find epochs that are very likely to be non-REM we identify every epoch where the SWA+Spindle signal is above a certain threshold. For example the average of the signal is used here as a threshold and we then keep the information of when those periods begin and end.
cfg = [];
cfg.artfctdef.threshold.channel = {'swa+spindle'};
cfg.artfctdef.threshold.bpfilter = 'no';
cfg.artfctdef.threshold.max = nanmean(data_continuous_perband_sum.trial{1}(5,:)); % mean of the 'swa+spindle' channel
cfg = ft_artifact_threshold(cfg, data_continuous_perband_sum);
% keep the begin and end sample of each "artifact", we need it later
nonREM_detected = cfg.artfctdef.threshold.artifact;
Given the information above about periods in the data with EOG activity, EMG artifacts and the estimates for non-REM we can now try to reconstruct a sleep hypnogram that estimates periods. This is of only a simple estimation but it is still useful for subsequent analyses and getting an overview about the changes in sleep states over the course of sleep.
% construct a hypnogram, Wake-0, Stage-1, Stage-2, Stage-3, Stage-4, REM-5
hypnogram = -1 * ones(1,numel(data_epoched.trial)); %initalize the vector with -1 values
%REM defined by the detected EOG activity
for i=1:size(EOG_detected,1)
start_sample = EOG_detected(i,1);
end_sample = EOG_detected(i,2);
start_epoch = ceil((start_sample)/(30*128));
end_epoch = ceil(( end_sample)/(30*128));
hypnogram(start_epoch:end_epoch) = 5; % REM
end
%Non-REM defined by EMG
for i=1:size(nonREM_detected,1)
start_epoch = nonREM_detected(i,1);
end_epoch = nonREM_detected(i,2);
hypnogram(start_epoch:end_epoch) = 2.5; % it could be any of 1, 2, 3 or 4
end
%Epochs with detected EMG artifacts are now again (re)labled as Wake
for i=1:size(EMG_detected,1)
start_sample = EMG_detected(i,1);
end_sample = EMG_detected(i,2);
start_epoch = ceil((start_sample)/(30*128));
end_epoch = ceil(( end_sample)/(30*128));
hypnogram(start_epoch:end_epoch) = 0; % wake
end
Sometimes the data is longer and does not add up to 30 sec epochs. For example the Subject05 data is 1 second (128 samples) longer than 1048 epochs. We might have introduced an epoch by artifacts that are in this one second that would be the 1049 epoch. but there is no full 30-second 1049 epoch. Thus we want to prune it again to 1048 trials. Here the data_orig.sampleinfo(2) contains the number of samples in the original data
% prune the hypnogram to complete 30-sec epochs in the data
% discarding the rest at the end
number_complete_epochs = floor(data_orig.sampleinfo(2)/(30*128));
hypnogram = hypnogram(1:number_complete_epochs);
Lets load a prescored hypnogram as the reference
% Wake-0, Stage-1, Stage-2, Stage-3, Stage-4, REM-5, Movement Time-0.5
prescored = load([datapath filesep subjectdata.subjectdir filesep subjectdata.hypnogramfile])';
figure
plot([prescored-0.05; hypnogram+0.05]', 'LineWidth', 1); % shift them a little bit
legend({'prescored', 'hypnogram'})
ylim([-1.1 5.1]);
lab = yticklabels; %lab = get(gca,'YTickLabel'); %prior to MATLAB 2016b use this
lab(strcmp(lab, '0')) = {'wake'};
lab(strcmp(lab, '1')) = {'S1'};
lab(strcmp(lab, '2')) = {'S2'};
lab(strcmp(lab, '3')) = {'SWS'};
lab(strcmp(lab, '4')) = {'SWS'};
lab(strcmp(lab, '5')) = {'REM'};
lab(strcmp(lab, '-1')) = {'?'};
yticklabels(lab); %set(gca,'YTickLabel',lab) ; %prior to MATLAB 2016b use this
Now we want to view either the prescored or the estimated hypnogram information in with ft_databrowser using the feature to mark artifactual epochs to highlight epochs according to their sleep state. For simplicity, here we want to focus only on Wake, REM and non-REM because those sleep stages are the ones we get both from the prescored and our estimated hypnogram. However the prescored hypnogram can also give us a more detailed view on the non-REM sleep stages that we can take a look at in the browser
artfctdef = [];
if false % can either choose true or false here to switch between presocred and estimated hypnogram
epochs_wake = find(prescored == 0);
epochs_S1 = find(prescored == 1);
epochs_S2 = find(prescored == 2);
epochs_SWS = find(prescored == 3 | prescored == 4);
epochs_nonREM = find(prescored >= 1 & prescored <= 4);
epochs_REM = find(prescored == 5);
artfctdef.S1.artifact = [epochs_S1(:) epochs_S1(:)];
artfctdef.S2.artifact = [epochs_S2(:) epochs_S2(:)];
artfctdef.SWS.artifact = [epochs_SWS(:) epochs_SWS(:)];
else
epochs_wake = find(hypnogram == 0);
epochs_nonREM = find(hypnogram >= 1 & hypnogram <= 4);
epochs_REM = find(hypnogram == 5);
artfctdef.nonREM.artifact = [epochs_nonREM(:) epochs_nonREM(:)];
end
View it in the time-resolved spectral estimate each sample corresponding to a 30-second epoch
artfctdef.wake.artifact = [epochs_wake(:) epochs_wake(:)];
artfctdef.REM.artifact = [epochs_REM(:) epochs_REM(:)];
cfg = [];
cfg.continuous = 'yes';
cfg.artfctdef = artfctdef;
cfg.blocksize = 60*60*2;
cfg.viewmode = 'vertical';
cfg.artifactalpha = 0.7; % this make the colors less transparent and thus more vibrant
ft_databrowser(cfg, data_continuous_perband_sum);
Exercise 4
Optional Explore how the prescored hypnogram looks like in the databrowser with all the sleep stages (non only non-REM, REM and Wake but also S1, S2, and SWS). You can switch the ‘if false’ to ‘if true’ above.
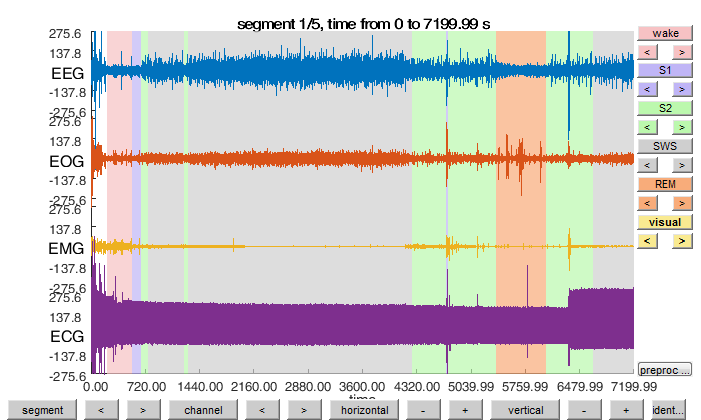
View it then together with the original data after adjusting the hypnograms from the 30-second time scale to the 128 Hz sampling rate.
% in the original data there are 30*128 samples per epoch
% the first epoch is from sample 1 to sample 3840, etc.
artfctdef = [];
artfctdef.wake.artifact = [(epochs_wake(:) -1)*30*128+1 (epochs_wake(:) +0)*30*128];
%artfctdef.S1.artifact = [(epochs_S1(:) -1)*30*128+1 (epochs_S1(:) +0)*30*128];
%artfctdef.S2.artifact = [(epochs_S2(:) -1)*30*128+1 (epochs_S2(:) +0)*30*128];
%artfctdef.SWS.artifact = [(epochs_SWS(:) -1)*30*128+1 (epochs_SWS(:) +0)*30*128];
artfctdef.nonREM.artifact = [(epochs_nonREM(:)-1)*30*128+1 (epochs_nonREM(:)+0)*30*128];
artfctdef.REM.artifact = [(epochs_REM(:) -1)*30*128+1 (epochs_REM(:) +0)*30*128];
cfg = [];
cfg.continuous = 'yes';
cfg.artfctdef = artfctdef;
cfg.blocksize = 60*60*2;
cfg.viewmode = 'vertical';
cfg.artifactalpha = 0.7;
ft_databrowser(cfg, data_continuous);
Store the hypnogram in the epoched data as “trialinfo”. In a cognitive experiment the epochs/trials would be ~1 second and each would have a condition code. Here the epochs/trials are 30 seconds and each has the sleep stage as code.
data_epoched.trialinfo = hypnogram(:);
Event detection during sleep
Other than detecting periods of hightened or lowered activity often it is interesting to detect discrete short, transient events in the signals. During sleep we can for example detect events like QRS complexes in the ECG (where we use the RR-interval to define the heart rate), or EEG events like slow waves (single waves of about 0.5 to 2 Hz which have a high amplitude of about 75 uV), sleep spindles (transient waxing and waning events of about 0.5 to 2 seconds duration and 15 to 50 uV maximal amplitude). Note that for simplicity we do not make any distinction between slow-waves, K-complexes or slow oscillations but lump them all together. For example the precise temporal relationship and (phase-locking) and shape of sleep spindles within slow waves is a good indicator for the success of the consolidation of memory during sleep and has become a target that can be influenced during the night to affect our memory. First we practice how to detect a very well defined event, the QRS complex, and then we take a look at more arbitrarily defined events like slow-waves and sleep spindles and see if they interact within the same modality (EEG) and across modalities (EEG and ECG/EKG).
R-waves and heart rate in ECG
Detect R-waves using ft_artifact_zvalue by filtering in a frequency band that puts an emphasis on the R-waves frequency in the ECG. As R-waves are concrete peaks we find the maxima in the envelope of the envelope signals. Note that this methods also works if the R-waves would be inverted pointing towards the negative values.
%% find heart R-waves in ECG
cfg = [];
cfg.continuous = 'yes';
% channel selection, cutoff and padding
cfg.artfctdef.zvalue.channel = 'ECG';
cfg.artfctdef.zvalue.cutoff = 0.5;
cfg.artfctdef.zvalue.trlpadding = 0;
cfg.artfctdef.zvalue.fltpadding = 0;
cfg.artfctdef.zvalue.artpadding = 0.1;
% algorithmic parameters
cfg.artfctdef.zvalue.bpfilter = 'yes';
cfg.artfctdef.zvalue.bpfreq = [20 45];
cfg.artfctdef.zvalue.bpfiltord = 4;
cfg.artfctdef.zvalue.bpfilttype = 'but';
cfg.artfctdef.zvalue.hilbert = 'yes';
cfg.artfctdef.zvalue.boxcar = 0.2;
cfg.artfctdef.zvalue.artfctpeak = 'yes'; % to get the peak of the R-wave
% make the process interactive
cfg.artfctdef.zvalue.interactive = 'yes';
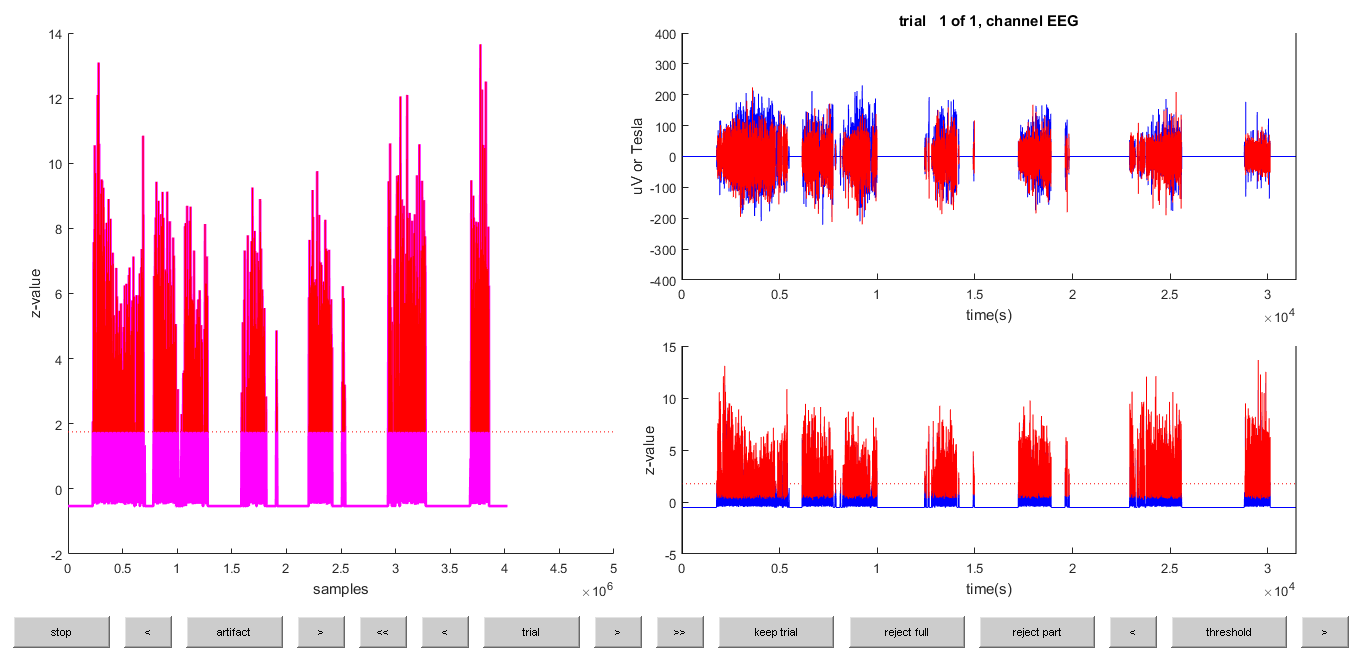
cfg = ft_artifact_zvalue(cfg, data_continuous);
Safe when (the samples of the R-waves occur for later
Rwave_peaks = cfg.artfctdef.zvalue.peaks;
The R-peaks are difficult to see, since there are so many (>35000 heart beats during one night) use the MATLAB magnifying glass to zoom in. Also it might be that the signal was recored in the opposite direction, that is the R-waves would be pointing down rather than up (which is the case here point downwards). In this case the signal could be inverted by multiplying this channel’s data with -1. For example:
data_continuous.trial{1}(4,:) = -1 * data_continuous.trial{1}(4,:)
Check if the detected peaks are good estimates of the R-wave in the ft_databrowser
artfctdef = [];
artfctdef.rwave.artifact = [Rwave_peaks-10 Rwave_peaks+10];
cfg = [];
cfg.continuous = 'yes';
cfg.artfctdef = artfctdef;
cfg.blocksize = 60;
cfg.viewmode = 'vertical';
cfg.artifactalpha = 0.7;
ft_databrowser(cfg, data_continuous);
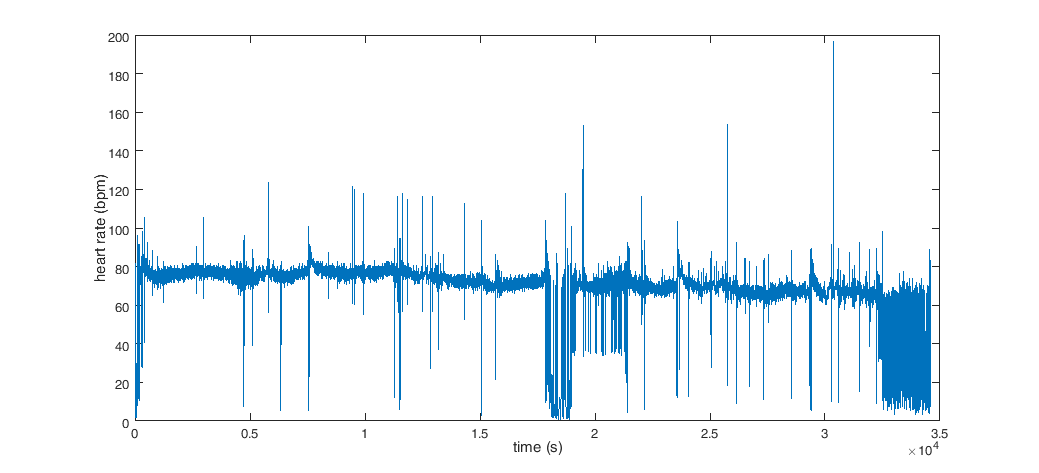
From this R-wave samples we can also compute a continuous heart rate signal.
heart_rate = 60 ./ (diff(Rwave_peaks') ./ data_continuous.fsample);
% determine the time in seconds of each detected beat
heart_time = Rwave_peaks / data_continuous.fsample;
% let us place the heart rate in between the beats
heart_time = (heart_time(1:end-1) + heart_time(2:end)) / 2;
figure;
plot(heart_time, heart_rate)
xlabel('time (s)');
ylabel('heart rate (bpm)');
Sleep spindles and slow waves in EEG
Filter for non-REM data for detection
Before we can detect concrete events in non-REM we need to prepare the data for this analysis by excluding all the epochs from the data that would interfere with our detection method. First we discard all trials that are wake or REM from the information of the hypnogram we stored previously in the trialinfo of the epoched data. since spindles and non-REM mostly occur during Stages 2, 3 and 4 this is the epochs we want to focus on (Stage 1 by definition does not contain sleep spindles or slow waves). Here you can choose if you want to contine with the information of the prescored hypnogram or our estimated one.
cfg = [];
cfg.trials = (data_epoched.trialinfo >= 2 & data_epoched.trialinfo <= 4); % Only non-REM stages, but not Stage 1
data_epoched_nonREM = ft_selectdata(cfg, data_epoched);
Reconstruct the original continuous data since the wake and REM data is not present any more, that will be filled with nans.
cfg = [];
cfg.trl(1,1) = data_continuous.sampleinfo(1);
cfg.trl(1,2) = data_continuous.sampleinfo(2);
cfg.trl(1,3) = 0;
data_continuous_nonREM = ft_redefinetrial(cfg, data_epoched_nonREM);
% replace the nans with zeros
selnan = any(isnan(data_continuous_nonREM.trial{1}), 1);
data_continuous_nonREM.trial{1}(:,selnan) = 0;
Lets view the prepared non-REM data
cfg = [];
cfg.continuous = 'yes';
cfg.blocksize = 60*60*2;
cfg.viewmode = 'vertical';
ft_databrowser(cfg, data_continuous_nonREM);
Slow-wave or sleep spindle detection in EEG
Candidates for slow waves or sleep spindle events can be detected using ft_artifact_zvalue similarly like for detecting the R-waves above but using a good low and high pass or the band-pass filter in the slow-wave or spindle band and a more strict cutoff threshold.
cfg = [];
cfg.continuous = 'yes';
% channel selection and padding
cfg.artfctdef.zvalue.channel = 'EEG';
cfg.artfctdef.zvalue.trlpadding = 0;
cfg.artfctdef.zvalue.fltpadding = 0;
cfg.artfctdef.zvalue.artpadding = 0.1;
% cutoff and algorithmic parameters
cfg.artfctdef.zvalue.cutoff = 1.75; % 1.75 for both slow waves and spindles
cfg.artfctdef.zvalue.bpfilter = 'yes';
cfg.artfctdef.zvalue.bpfiltord = 4;
cfg.artfctdef.zvalue.bpfilttype = 'but';
if true % true for slow-waves, false for spindles
cfg.artfctdef.zvalue.bpfreq = [0.5 4];
else
cfg.artfctdef.zvalue.bpfreq = [12 15];
end
cfg.artfctdef.zvalue.hilbert = 'yes';
cfg.artfctdef.zvalue.boxcar = 0.2;
cfg.artfctdef.zvalue.artfctpeak = 'yes'; % to get the peak of the event envelope
% make the process interactive
cfg.artfctdef.zvalue.interactive = 'yes';
[cfg, ] = ft_artifact_zvalue(cfg,data_continuous_nonREM);
Exercise 5
The threshold here is key for the proper detection, the value here is based on experience. Try to use a more strict (higher) threshold and see if the results later on change.
Safe the detected candidate events for later with their beginnings and ends (spindle_detected) and calculating their duration.
event_detected = cfg.artfctdef.zvalue.artifact;
event_peaks = cfg.artfctdef.zvalue.peaks;
event_duration = (event_detected(:,2)-event_detected(:,1)+1) ./ data_continuous_nonREM.fsample;
By definition valid slow waves or sleep spindles have a minimum and maximum duration that we want to filter the candidate events for
% find slow waves/spindles only with the right duration of 0.5 to 2 seconds
duration_min = 0.5;
duration_max = 2;
valid_events_index = ((event_duration > duration_min) & (event_duration < duration_max));
%update our event information accodingly with the valid slow waves or sleep spindles.
event_detected = event_detected(valid_events_index,:);
event_peaks = event_peaks(valid_events_index);
event_duration = event_duration(valid_events_index);
Let’s see how many slow waves or sleep spindles we found and if they are of the right duration (~1 second, on average can be longer for slow waves, and shorter on for spindles).
%number of events
numel(event_peaks)
%mean event duration
mean(event_duration)
Often, to check if we get the right kind of event, at least on average, it is very helpful to look at the average sleep slow wave or sleep spindle. For this we need a good offset at which our events can be aligned, so that when averaged the variable signal do not cancel each other out. Other than for ERPs, where we might have recored event markers, we need to find such offsets ourselves in for spontaneous detected events. Often a clear minimum or maximum in the event with the highest or lowest amplitude in a narrow time window (around the center) is a good candidate as an offset, as this is the most consistent time point between such events. For sleep spindles and slow waves the minimum peak of the highest amplitude is typically chosen for this.
%%% get the trials to get the data +-1 second around the envelope
%%% peak that we detected
cfg = [];
cfg.channel = {'EEG'};
data_continuous_nonREM_EEG = ft_selectdata(cfg,data_continuous_nonREM);
% filter the data in the slow wave or spindle band to remove non-event noise
cfg.bpfilter = 'yes';
if true % true for slow-waves, false for spindles
cfg.bpfreq = [0.5 4];
else
cfg.bpfreq = [12 15];
end
data_continuous_nonREM_EEG_event_filtered = ft_preprocessing(cfg,data_continuous_nonREM_EEG);
% redefine the trial with the offset preserving timepoint from beginning of the raw data
search_offset = data_continuous_nonREM.fsample% +-1 seconds around the center
cfg.trl = [event_peaks-search_offset event_peaks+search_offset -search_offset+event_peaks];
data_continuous_nonREM_EEG_event_filtered_temp = ft_redefinetrial(cfg,data_continuous_nonREM_EEG_event_filtered);
% find the minimums within the trials
event_trial_minimums = cellfun(@(signal) find(signal == min(signal),1,'first'),data_continuous_nonREM_EEG_event_filtered_temp.trial);
% update the times from the time points with respect to the original raw data
event_minimum_times = event_trial_minimums;
for iTrialSpindle = 1:numel(data_continuous_nonREM_EEG_event_filtered_temp.trial)
event_minimum_times(iTrialSpindle) = data_continuous_nonREM_EEG_event_filtered_temp.time{iTrialSpindle}(event_trial_minimums(iTrialSpindle));
end
%get the samples of the minimum sleep spindle signals (troughs)
event_minimum_samples = round(event_minimum_times*data_continuous_nonREM.fsample);
Redefine the trial with the offset at the time of the filtered spindle signal minimum
% a buffer we need to have padding left and right to make nice
% time-frequency graph later on
padding_buffer = 4*data_continuous_nonREM.fsample; % 8 seconds
cfg = [];
cfg.trl = [event_minimum_samples'-data_continuous_nonREM.fsample-padding_buffer event_minimum_samples'+data_continuous_nonREM.fsample+padding_buffer repmat(-(data_continuous_nonREM.fsample+padding_buffer),numel(event_minimum_samples),1)];
data_continuous_nonREM_EEG_events = ft_redefinetrial(cfg,data_continuous_nonREM_EEG);
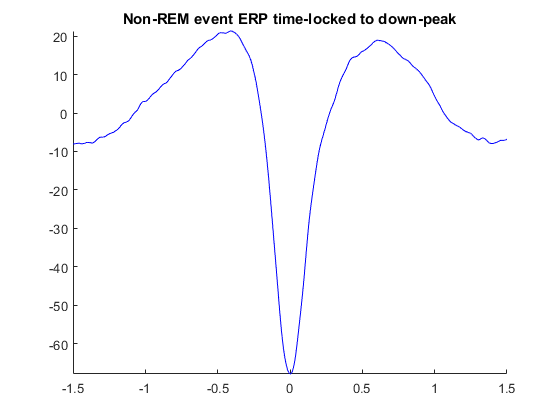
View the event average signal time-locked to the trough.
Sanity check
Does the amplitude match to the definition of slow waves (minimum amplitude of 75 microVolts)? The signal before sleep spindles starts with a negative potential and at the end of spindles is more positive, what can this tell us of the temporal occurrence of sleep spindles with respect to slow waves?
The polarity of the signal matters. Does the activity that we time-lock give us confidence that the data was actually recorded or read in with the right polarity of the EEG channels, for example sometimes channels are unintentionally inverted, that is slow waves, spindles or epileptic spikes etc. would appear in the “wrong” direction because we then detect them here by the negative trough of the signal. This also depends on the referencing of the electrodes for used channel.
figure
cfg = [];
[timelock] = ft_timelockanalysis(cfg, data_continuous_nonREM_EEG_events);
cfg = [];
cfg.xlim = [-1.5 1.5];
cfg.title = 'Non-REM event ERP time-locked to down-peak';
ft_singleplotER(cfg,timelock)
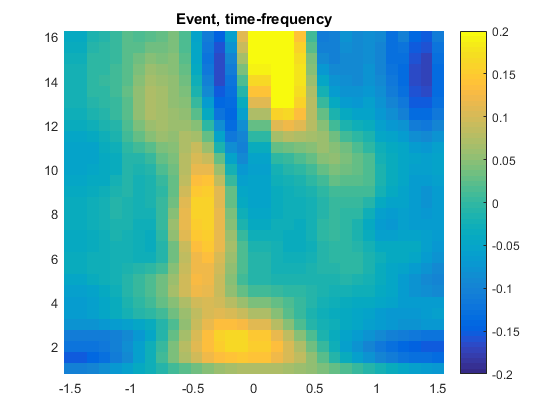
Calculate the event-related Time-Frequency (ERF) around the event time-locked to the trough.
cfg = [];
cfg.channel = 'EEG';
cfg.method = 'wavelet';
cfg.length = 4;
cfg.foi = 1:0.5:16; % 0.5 Hz steps
cfg.toi = [(-padding_buffer-1.5):0.1:(1.5+padding_buffer)]; % 0.1 s steps
event_freq = ft_freqanalysis(cfg, data_continuous_nonREM_EEG_events);
Visualize the event-related time-frequency around the event time-locked to the trough. What activity other than the frequency band that is not in the frequency band used for detection, when does it typically occur, before, after, or during the event.
% view the time-frequency of a slow wave or spindle event
figure
cfg = [];
cfg.baseline = [-1.5 1.5]; % a 3 s baseline around the event as it has no clear start or end.
cfg.baselinetype = 'normchange';
cfg.zlim = [-0.2 0.2];
cfg.xlim = [-1.5 1.5];
cfg.title = 'Event, time-frequency';
ft_singleplotTFR(cfg,event_freq);
View the detected events in the original data.
cfg = [];
cfg.continuous = 'yes';
cfg.viewmode = 'vertical';
cfg.blocksize = 60; %view the data in 30-s blocks
cfg.event = struct('type', {}, 'sample', {});
cfg.artfctdef.event.artifact = event_detected;
%cfg.artfctdef.slow_waves.artifact = event_detected;
%cfg.artfctdef.spindles.artifact = event_detected;
cfg.artfctdef.eventpeaks.artfctpeak = event_minimum_samples;
cfg.plotevents = 'yes';
ft_databrowser(cfg, data_continuous_nonREM);
Exercise 6
Repeat the above analysis for event detection for sleep spindles when you did slow waves and vice versa. For this you need to switch between two last occurrances from or to “if true” or “if false”.
Exercise 7
View the outcomes of the slow-wave and spindle detection in the same window of ft_databrowser
Exercise 8
Repeat the tutorial or parts of it with the other dataset of Subject05, are there any differences in the data and the detection of events?
Exercise 9
Try to visualize an average QRS complex around the R-wave like was done for sleep slow waves and spindles. What kind of epochs/artifacts would you exclude here from the analysis?
Summary and suggested further reading
In this tutorial we learned how to read and interpret continuous sleep data. We learned how to use modalities EMG, EOG, EEG and ECG to gain more information about the changing states during a long recording. We used EMG and EOG to find epochs of Wake that we considered artifacts for further analysis of non-REM sleep.
Also we looked at the distribution of different sleep frequency bands, their fluctuation in sleep cycles and how we can extract epochs from the data that contains useful information for further analysis while at the same time deciding to exclude epochs with other (artifactual) activity (e.g., Wake). We thus constructed a partial estimate of a sleep profile (hypnogram) to aid us further.
Finally we explored how easy it is to detect spontaneous events in signals like ECG and EEG by using simple filtering and thresholding of the cleaned data epochs as a basis, e.g., we found R-waves, sleep slow waves and spindles. These have been then viewed in the ft_databrowser and we looked at the typical spontaneous events by aligning them by time (ERP) and look at time-locked frequency activity (ERF), all in a single channel.
This should give you a basis of also recognizing other data and see that recordings are highly dependent on the current state. Importantly, this might also apply to wake recordings of task in which the subjects might doze off, loose focus or have their eyes closed or directed away at important periods of the task. The techniques here can thus also be used as sanity check in other data.
Interesting to continue the analysis if you want to go further:
- do the analyis on data with multiple EEG channels and topographic plots (e.g., Time-frequency analysis of combined MEG/EEG data)
- using ft_freqgrandaverage and ft_timelockgrandaverage to average the results of different recordings/subjects
- Practicing or trying to automatically find different kind of events, e.g., rapid eye movements and blinks (in the first derivative of a filtered EOG signal), epileptic spikes have similar properties to slow waves (but have different amplitudes and shapes) …
- find the timelocking/co-occurrence between different events (e.g., spindles that occur at the same time as slow waves.) and only look at the ones that occur together or the ones that do not.
Suggested tutorials for further reading:
- Preprocessing - Reading continuous EEG data
- Getting started with EDF (European Data Format) data
- Creating a clean analysis script and batch processing
- Time-frequency analysis
- Time-frequency analysis of combined MEG/EEG data
Suggested frequently asked questions: