Preprocessing and analysis of spike-train data
Introduction
In this tutorial you find information about preprocessing and analysis of spike data, that is isolated single-unit or multi-unit activity. We explain the format by which we represent spike data and demonstrate how to compute
- descriptive statistics of action potential waveforms
- inter spike interval distributions (and visualization)
- peri-stimulus time histograms (and their visualization)
- raster plots
- spike densities
- average firing rates
- auto- and cross-correlations between spike trains
- joint peri stimulus time histograms (and visualization)
For this analysis, we will use a monkey dataset recorded by Pascal Fries and colleagues (Fries et al., 2001, Science; Fries et al, 2008, Journal of Neuroscience). In this experiment, LFPs and spikes were recorded from V4 while monkeys performed a visual attention task. A moving stimulus grating was presented in the recorded neurons’ receptive fields, and another stimulus was presented outside the recorded neurons’ receptive fields. In a given trial, the grating stimulus in the receptive field was either attended (attention inside the receptive field) or not attended (distractor; attention outside the receptive field). In this tutorial, we analyze the spike data around the presentation of the stimulus until the time of the first stimulus change (of either distractor or target). We also show how to read in an M-clust .t file from a CA1 hippocampus cell, recorded while a rat explored a maze.
Background
Neurons transmit information to each other by means of trains of action potentials, also called spikes. These spikes can be identified by placing microelectrodes in the extracellular or intracellular medium and recording the electric potential difference between the signal and reference electrode. This recorded voltage is then band-pass filtered (spikes have the bulk of their signal energy between 300-6000 Hz) to remove large-amplitude, slow (LFP) voltage fluctuations (on the order of milliVolts) caused by dendritic currents and electric artifacts. Spikes are then detected on- or offline by setting a threshold on the band-pass filtered voltage trace. This threshold typically lies somewhere between 30-100 microVolt (as a comparison: electric noise in the band-pass filtered signal typically does not exceed 10-15 microVolt). Sometimes, an additional threshold is used on the slope of the voltage traces. Each time the band-pass filtered voltage crosses the action potential threshold the recording system registers the time of the threshold crossing. Recording systems do not have a continuous representation of time at their disposal but measure time in discrete time intervals, called timestamps. Hence, we refer to the times of voltage threshold crossing as timestamps. For every threshold crossing, a small segment of about a 1-2 milliseconds of the voltage trace around the time of threshold crossing is stored at a high sampling frequency (>20000 Hz). If the voltage threshold crossing was caused by the upstroke of a neuron’s action potential, then this small segment of the voltage trace contains the action potential voltage trajectory, superimposed on voltage fluctuations caused by electric noise and other neurons’ firing. We refer to these 1-2 milliseconds voltage snippets as waveforms.
The set of timestamps and their corresponding waveforms are then subsequently processed by spike sorting, that is the identification of isolated clusters of similar waveforms that correspond to single neuronal sources, called ‘single-unit activity’. Sometimes, neurophysiologists reject only the noisy waveforms and refer to the remaining set of spikes as ‘multi-unit activity’. An important aspect of single cell analysis is the description of action potential waveforms, because these are informative about the cell type that the recorded neuron corresponds to (e.g., see Bartho et al., 2004; Mitchell & Reynolds, 2007).
The spike trains can be represented by either a vector of timestamps (e.g., [3003 30020 30050] etc.) (a ‘point representation’) or by a binary vector of zeros and integers (if the sample rate is not high enough, sometimes a value higher than 1 may occur) at a certain sample rate (e.g., [010001000001] etc., where a 1 indicates a spike for a given sample and every bin corresponds to 1/fsample seconds). The disadvantage of the binary representation is that is quite memory inefficient and not particularly suited for many spike train analyses that are based on computations on the spike times. However, some computations are more efficient when data is represented in a binary format, for example the computation of spike densities (see below).
Typically, action potentials are considered as all-or-nothing events, based on the conventional assumption that the shape of the action potential is not a feature by which neurons transmit information. Given this assumption, spike trains can be considered as point processes. A standard analysis to characterize the statistics of the point process is by analyzing the inter spike interval distribution, which typically follows a gamma or exponential distribution, and by examining the inter spike interval return plots (the current inter spike interval versus the next inter spike interval), which reveals the second order statistics of the inter spike interval distribution (see Dayan & Abbott, Theoretical Neuroscience, 2001). Often, neurophysiologists ignore the temporal structure of the spike trains and consider only the the number of spikes per time period, that is the firing rate. The statistics of the spike count typically follows a Poisson distribution.
A common approach to investigate the information content of the spike train is then to examine the relationship between the firing rate as a function of time relative to an external stimulus variable. A neuron’s firing rate at a particular moment can be modeled as a probability density function that specifies the expected number of action potentials per second in a limited time interval. This probability density function can be estimated by computing the peri stimulus time histogram (PSTH), that is the number of spikes per discrete time bin around the stimulus event. A more continuous measure of the probability density function can be obtained by convolving the spike trains with some kernel, for example a Gaussian kernel.
Neurons often fire in synchrony, meaning that action potentials from different neurons tend to co-occur in time. This synchrony may be the result of task-induced fluctuations in the firing rate (Brody, 1999) or oscillatory coupling (Gray et al., 1989). Oscillatory coupling and synchrony between spike trains can be investigated by computing the cross-correlation function between spike trains, that is the probability or frequency by which two action potentials from two different neurons occur at a certain delay. The joint peri stimulus time histogram (see Brown et al., 2004; Aertsen et al., 1987; Perkel et al., 1967) quantifies the cross-correlation function as a function of time relative to stimulus onset. To investigate whether the structure of the cross-correlation function is caused by task-induced fluctuations of the firing rate, or by temporal coordination that is not time-locked to stimulus onset, one typically uses a shuffle correction in which the order of subsequent trials is shuffled. The resulting ‘shuffle-corrected’ cross-correlation is then solely driven by task-induced fluctuations in the firing rate.
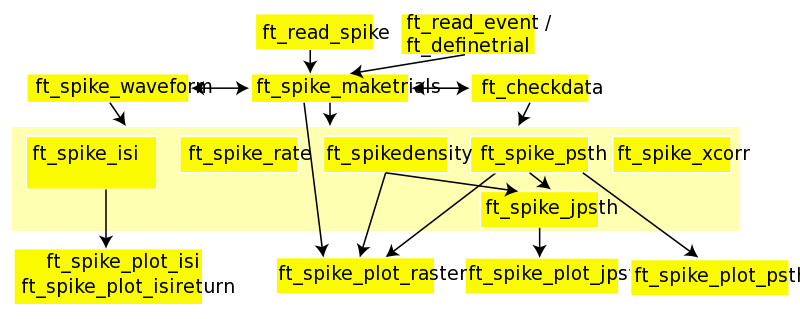
Procedure
- Read the spike data into MATLAB using ft_read_spike
- Create a trial structure for the spike trains using using ft_read_event and ft_spike_maketrials.
- Converting spike structure into continuous raw structure, and back, using ft_checkdata
- Computation of inter spike interval distribution, and its visualization, using ft_spike_isi and ft_spike_plot_isireturn.
- Computation of the mean and variance of the action potential waveform, using ft_spike_waveform.
- Computation of peri stimulus time histogram, using ft_spike_psth.
- Computation of spike-densities, using ft_spikedensity.
- Visualization of spike trains, using ft_spike_plot_raster.
- Computing average firing rates and correlations between neuronal firing rates, using ft_spike_rate.
- Compute cross-correlation function between neurons using ft_spike_xcorr
- Compute joint peri-stimulus time histograms, and their visualization, using ft_spike_jpsth and ft_spike_plot_jpsth.
Reading in spike data
Make sure you run ft_defaults after having added the main FieldTrip path (e.g., addpath(‘path_to_fieldtrip’)), ensuring that the required functions are in your MATLAB path. For spike analysis there is spike toolbox that is located in fieldtrip/contrib/spike.
Spike data can be read out using the function ft_read_spike. At the time of writing this tutorial the supported formats are neurosim, mclust t files, neuralynx (nse, nst, ntt, nts) and plexon (nex and plx) files. The original data can be downloaded here. After reading out the spike data, we select the spike channels of interest.
spike = ft_read_spike('p029_sort_final_01.nex');
cfg = [];
cfg.spikechannel = {'sig002a_wf', 'sig003a_wf'}; % select only the two single-units
spike = ft_spike_select(cfg, spike);
One obtains a so called spike structure (see ft_datatype_spike). In this spike structure we simply gather the raw spike data (timestamps of spikes and waveforms) for multiple cells, which are identified through their label:
spike =
label: {'sig002a_wf' 'sig003a_wf'}
timestamp: {[1x164456 int32] [1x134803 int32]}
waveform: {[1x32x164456 double] [1x32x134803 double]}
unit: {[1x164456 double] [1x134803 double]}
hdr: [1x1 struct]
dimord: '{chan}_lead_time_spike'
cfg: [1x1 struct]
The spike structure contains a representation of timestamps, waveform and labels for a number of cells (N = 2). The field spike.label is an 1 x N cell-array containing a character string that identifies each cell. For each of the N units, the field spike.timestamp contains the spike timestamps, where one timestamps corresponds to 1/40000 seconds in this case, as can be seen from spike.hdr.FileHeader.Frequency (and would correspond to microseconds for the Digital Neuralynx, for example).
For example, 164456 spikes were recorded for the isolated single-unit ‘sig002a_wf’.
The (optional) waveform field spike.waveform contains the waveform information for each of the spikes.
The first dimension of spike.waveform{i} is ‘leads’. For tetrode recordings, multiple leads per electrode are available, in which case the first dimension of spike.waveform{i} would have been of size 4.
The second dimension of waveform contains the samples. In this case one sample corresponds to 1/40000 seconds.
The third dimension of spike.waveform{i} equals the length of spike.timestamp{i}, such that a waveform is present for every spike (‘spike’ dimension).
The waveforms can be processed further using ft_spike_waveform.
Computing average waveforms
An important tool to characterize the particular cell class a recorded neuron belongs to, is the analysis of its action potential waveform. For example, pyramidal cells have broad waveforms, while fast spiking inhibitory interneurons have narrow waveforms (i.e., short peak-to-through duration of action potential). For characterizing waveforms we use the function ft_spike_waveform. The function ft_spike_waveform preforms alignment of waveforms based on the peak, such that they can also be aligned across different units, normalizes them to unit amplitude (if requested), interpolates the waveforms and performs outlier rejection. It also returns a spike structure (if two outputs are requested) in which the rejected outlier waveforms have been removed. Hence, it can be used as an additional preprocessing step. We ru
cfg = [];
cfg.fsample = 40000;
cfg.interpolate = 1; % keep the density of samples as is
[wave, spikeCleaned] = ft_spike_waveform(cfg,spike);
The resulting wave structure has the following content
wave =
time: [1x67 double]
avg: [2x1x67 double]
dof: [2x1x67 double]
var: [2x1x67 double]
label: {'sig002a_wf' 'sig003a_wf'}
dimord: 'chan_lead_time'
cfg: [1x1 struct]
and the structure spikeCleaned contains fewer spikes than originally now. In addition, the individual waveforms have been aligned:
spikeCleaned =
label: {'sig002a_wf' 'sig003a_wf'}
timestamp: {[1x160130 int32] [1x123007 int32]}
waveform: {[1x67x160130 double] [1x67x123007 double]}
unit: {[1x160130 double] [1x123007 double]}
hdr: [1x1 struct]
dimord: '{chan}_lead_time_spike'
cfg: [1x1 struct]
waveformtime: [1x67 double]
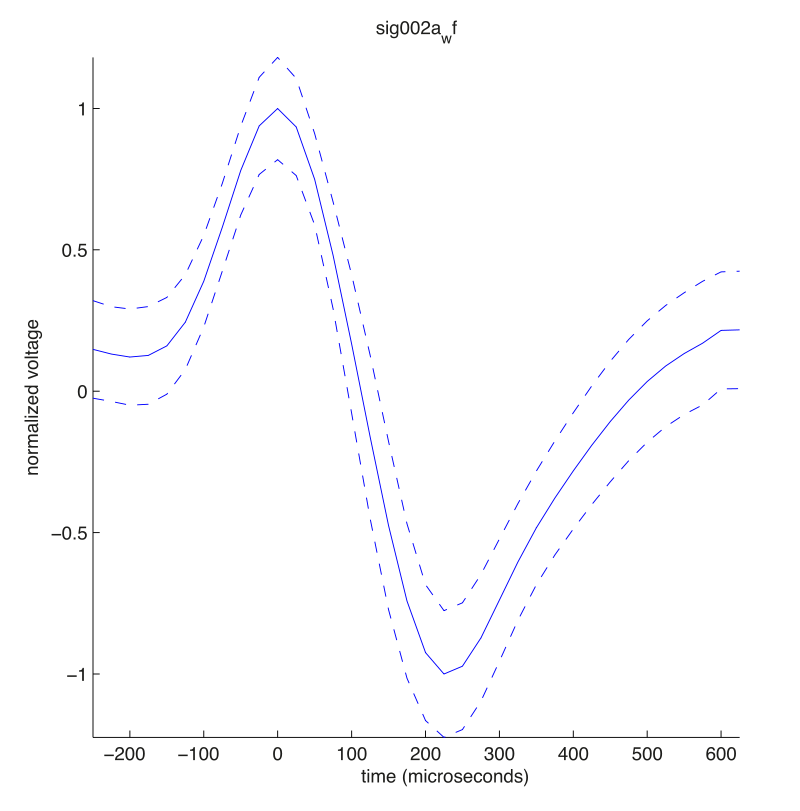
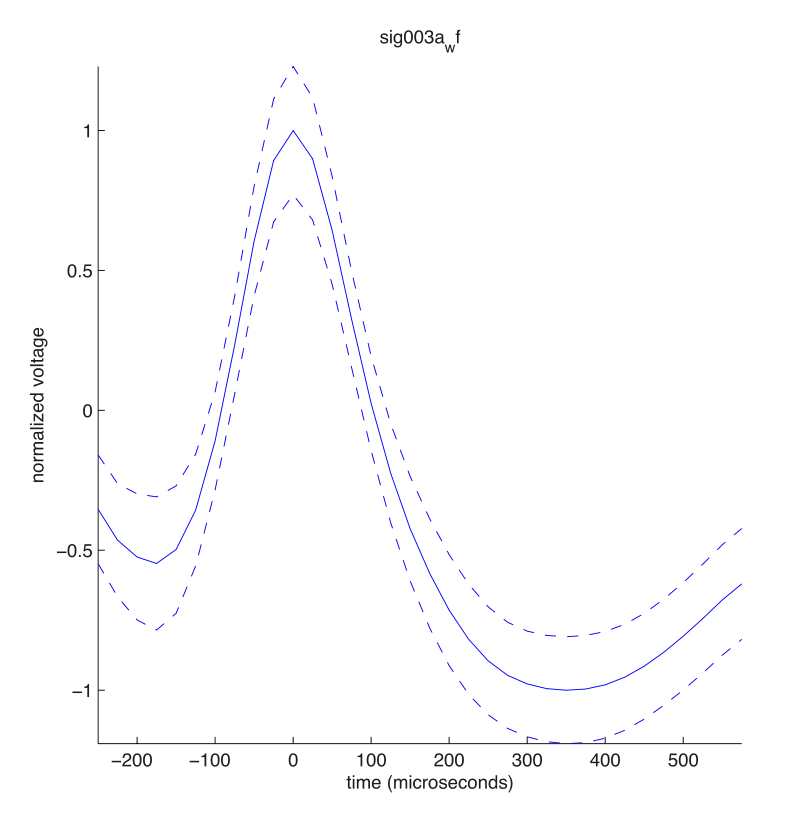
Plotting the mean waveform and variance for two units:
for k = [1 2]
figure,
sl = squeeze(wave.dof(k,:,:))>1000; % only keep samples with enough spikes
plot(wave.time(sl), squeeze(wave.avg(k,:,sl)),'k') % factor 10^6 to get microseconds
hold on
% plot the standard deviation
plot(wave.time(sl), squeeze(wave.avg(k,:,sl))+sqrt(squeeze(wave.var(k,:,sl))),'k--')
plot(wave.time(sl), squeeze(wave.avg(k,:,sl))-sqrt(squeeze(wave.var(k,:,sl))),'k--')
axis tight
set(gca,'Box', 'off')
xlabel('time')
ylabel('normalized voltage')
end
shows that one unit has the structure of a fast spiking cell (as its waveform is narrow), and one unit of a broad spiking cell (as its waveform is broad):
Adding trigger event information to spike structure
After the raw spike data has been read in, we restructure it relative to event triggers, that is we add a trial dimension to it. This serves two functions. Firstly, it converts the spike times in timestamp units to spike times in units of seconds. Secondly, by making trials, we can proceed with further analyses that relate the spiking to the experimental manipulation in each trial, such as peri stimulus time histograms (PSTHs), raster plots etc.. To this end, we use the function ft_spike_maketrials. This function requires two (cfg) configurations. Firstly, the number of timestamps per second, which must be explicitly specified by the user. This information is usually available in spike.hdr. In this case, cfg.timestampspersecond = spike.hdr.FileHeader.Frequency = 40000.
Secondly, an nTrials x 3 cfg.trl matrix containing start (:,1) (first column) and end (:,2) (second column) of the trials in timestamp units and the offset relative to the trigger (:,3) in timestamps units. This requires the event file to be read out. The event information is read from the file using:
event = ft_read_event('p029_sort_final_01.nex')
which returns
event =
37689x1 struct array with field
sample
value
timestamp
type
duration
offset
This specifies for each of the 37689 recorded events the sample (if available: this corresponds to the LFP samples, see the spike-field tutorial), the value (a number uniquely identifying the event) and the timestamp at which it occurred.
Using the value and timestamp fields, we built a user-specified function that constructs a cfg.trl matrix. In this case, we take -2.75 before stimulus onset until the first change of the stimulus. We first create a trial function that needs to be saved in the MATLAB path.
function trl = trialfun_stimon(cfg)
hdr = ft_read_header(cfg.dataset);
event = ft_read_event(cfg.dataset);
correctresponse = 10041;
begintrial = 10044;
endtrial = 10045;
stimon = 10030;
distractorChange = 12000;
targetChange = 12001;
attCnds = 20001:20004; % att in/out by target change first/second
E = struct2cell(event);
% replace empty cells with nan, otherwise the values are shifted
sel = cellfun(@isempty, E(:));
E(sel) = {nan};
samples = cell2mat(E(1,:)); % now in vector form
value = cell2mat(E(2,:));
timestamps = cell2mat(E(3,:)); % now in vector form
begmark = find(value==begintrial); % loop through the trial beginnings
endmark = find(value==endtrial); % loop through the trial beginnings
trl = [];
for k=1:length(begmark)
vals = value(begmark(k):endmark(k));
if any(ismember(vals,attCnds)) && ~isempty(find(vals==correctresponse))
ts = timestamps(begmark(k):endmark(k)); % in timestamp units
beginTs = ts(find(vals==stimon));
tsDistractor = ts(find(vals==distractorChange));
tsTarget = ts(find(vals==targetChange));
endTs = min([tsTarget(:);tsDistractor(:)]); % limit until first change
offset = - hdr.Fs*hdr.TimeStampPerSample*2.75; % 40000 timestamps per second x 2.75 sec
trl = [trl; [beginTs+offset endTs offset]];
end
end
For the purpose of walking through the tutorial, you should copy and paste the code above in the MATLAB editor and save the m-file as trialfun_stimon.m. Alternatively you can download the trial function here.
We then call ft_definetrial
cfg = [];
cfg.dataset = 'p029_sort_final_01.nex';
cfg.trialfun = 'trialfun_stimon';
cfg = ft_definetrial(cfg);
Running
cfg.timestampspersecond = spike.hdr.FileHeader.Frequency; % 40000
spikeTrials = ft_spike_maketrials(cfg,spike);
then gives us for this dataset a new structure
spikeTrials =
label: {'sig002a_wf' 'sig003a_wf'}
timestamp: {[1x83613 int32] [1x61511 int32]}
waveform: {[1x32x83613 double] [1x32x61511 double]}
unit: {[1x83613 double] [1x61511 double]}
hdr: [1x1 struct]
dimord: '{chan}_lead_time_spike'
cfg: [1x1 struct]
time: {[1x83613 double] [1x61511 double]}
trial: {[1x83613 double] [1x61511 double]}
trialtime: [600x2 double]
The structure now contains the spike times in seconds (spikeTrials.time) and in timestamp units (spikeTrials.timestamp) for the spikes that occurred in the specified trials (see that there are less spikes in spikeTrials.timestamp now than before).
We have created three new fields in the spike structure, namely spikeTrials.time, spikeTrials.trial and spikeTrials.trialtime.
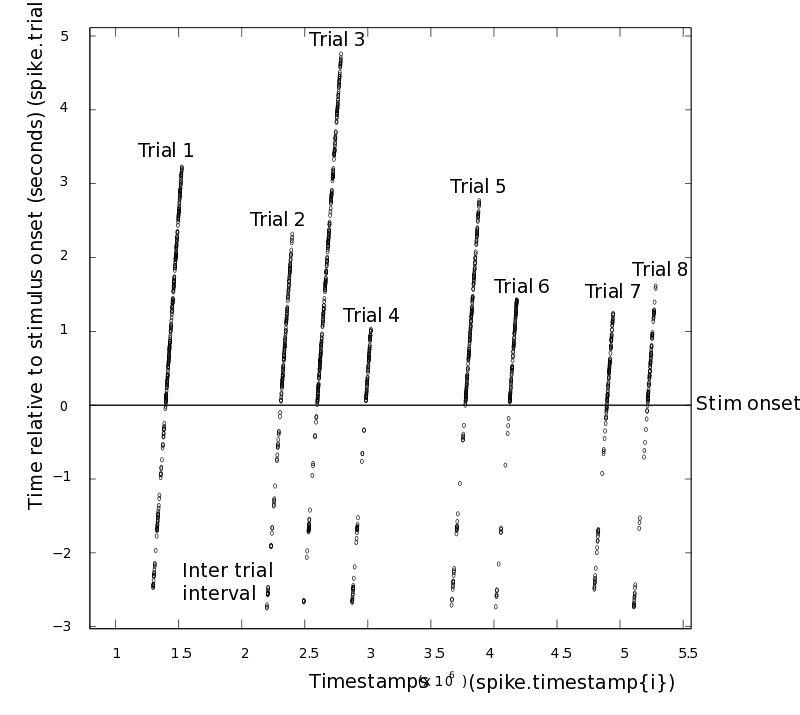
Together, these three fields fully identify the structure of the spiketrain relative to the event trigger. The relationship between spikeTrials.time{1} and spikeTrials.timestamp{1} is shown for the first 8 trials. All spikes that fall in the same trial have the same value in spikeTrials.trial{1}.
plot(spikeTrials.timestamp{1}, spikeTrials.time{1}, '.')
axis([1e6 5.5e6 -3 5])
In this example, unit ‘sig002a_wf’ fired in total 83613 spikes in the selected trial periods. For every spike, we indicate in trial the spike was fired (spikeTrials.trial) and at which time (in seconds) the spike was fired (spikeTrials.time). Thus, spikeTrials.time{i}(j), spikeTrials.trial{i}(j), spikeTrials.timestamp{i}(j), and spikeTrials.waveform{i}(:,:,j) all contain information about the j-th spike from the i-th neuron.
The spikeTrials.trialtime field fully specifies the structure of the spike trains relative to the experimental trials, as also it conveys in which trials no spike was fired, and what the borders of the trials were (as trials do not immediately start with a spike). The first and second column of spikeTrials.trialtime tell us what the start and end of the trial was relative to the event trigger.
For example,
spikeTrials.trialtime(1:5,:)
ans =
[ -2.750000 3.353600
-2.750000 2.318725
-2.750000 4.755700
-2.750000 1.051875
-2.750000 2.853950]
Note that the end of the trial is variable because we defined our trials running until the first target or distractor change. The field spikeTrials.cfg.trl tells us what the start and ends of the trials was in timestamps units.
spikeTrials.cfg.trl(1:5,:)
ans =
[ 1285920 1530064
2198387 2401136
2487745 2787973
2872531 3024606
3662529 3886687]
The advantage of the spike structure is that it is very memory efficient as compared to e.g., a binary (zeros and integers) format, and that data from hundreds of neurons can easily be stored in this structure. For many functions, e.g., PSTHs, raster-plots and cross-correlations, it is also the most natural format to perform computations. Furthermore, the format makes it easy to associate certain data with single spikes, for example spike-triggered LFP spectra and waveform information.
It is also possible to create only one trial. This is useful for two reasons. First of all, we explicitly convert timestamps to time. Secondly, we can correct for the fact the first recorded timestamp often does not start at zero (for example, with Neuralynx data).
In this case, the first recorded timestamp does correspond to zero. To this end, we run:
cfg = [];
hdr = ft_read_header('p029_sort_final_01.nex');
cfg.trl = [0 hdr.nSamples*hdr.TimeStampPerSample 0];
cfg.timestampspersecond = spike.hdr.FileHeader.Frequency; % 40000
spike_notrials = ft_spike_maketrials(cfg,spike);
to obtain the structure
spike_notrials =
label: {'sig002a_wf' 'sig003a_wf'}
timestamp: {[1x164445 int32] [1x134803 int32]}
waveform: {[1x32x164445 double] [1x32x134803 double]}
unit: {[1x164445 double] [1x134803 double]}
hdr: [1x1 struct]
dimord: '{chan}_lead_time_spike'
cfg: [1x1 struct]
time: {[1x164445 double] [1x134803 double]}
trial: {[1x164445 double] [1x134803 double]}
trialtime: [0 7.5560e+03]
Now, all spike_notrials.trial{i} are set to ones, and all spike times (spike_notrials.time) are relative to the onset of the recording.
Converting spike structure to continuous raw format and back
For some analyses, it may be desired to have the data in binary format. The spike structure can be converted to a continuous binary raw format (see ft_datatype_raw) by using:
dat = ft_checkdata(spikeTrials,'datatype', 'raw', 'fsample', 1000)
where fsample (in this case arbitrarily set at 1000 samples / sec) determines the desired spacing of samples. If fsample is too low compared to the spike firing rate, then the spike trains will not be binary (as multiple spikes can fall into one bin, resulting in integer values larger than one to keep track of the number of spikes in one sample) and the round-off errors will become larger. The structure data has the contents
dat =
trial: {1x600 cell}
time: {1x600 cell}
label: {'sig002a_wf' 'sig003a_wf'}
fsample: 1000
hdr: [1x1 struct]
cfg: [1x1 struct]
Each dat.trial{iTrial} contains a chan x time matrix with zeros at samples with no spikes and n at samples with n spikes. For example,
dat.trial{1}(:,4000:4004)
ans =
0 0 0 0 0
0 0 1 0 0
We can also convert the data structure back to a spike structure by using
spike_converted = ft_checkdata(dat,'datatype', 'spike')
After the conversion, the waveform and timestamp information is lost. Note that these conversions are automatically performed in all the spike functions, such that data in both a spike or (continuous) raw representation can be entered.
Characterizing inter-spike-interval (ISI) distributions
If spike trains are governed by a Poisson process, then the statistics of the spike train can be fully described: the distribution of waiting times between subsequent spikes is exponential, and the distribution of spike counts is Poisson. However, neurons show various non-Poissonian behaviors, such as refractory periods, bursting, and rhythmicity. These behaviors may arise from intrinsic dynamics (e.g., due to certain ion channel time constants), or from network processes (e.g., oscillations). To investigate whether the recorded spike trains reveal such non-Poissonian history effects, we study the ISI distribution.
For the current dataset, we study the ISI distribution for the stimulus period, using the functions ft_spike_isi and ft_spike_plot_isireturn. We compute the isi histogram using
cfg = [];
cfg.bins = [0:0.0005:0.1]; % use bins of 0.5 milliseconds
cfg.param = 'coeffvar'; % compute the coefficient of variation (sd/mn of isis)
isih = ft_spike_isi(cfg,spikeTrials);
The resulting structure isih has the following content
isih =
isi: {[1x83613 double] [1x61511 double]}
time: [1x200 double]
avg: [2x200 double]
dimord: 'chan_time'
label: {'sig002a_wf' 'sig003a_wf'}
coeffvar: [1.6898 1.1453]
cfg: [1x1 struct]
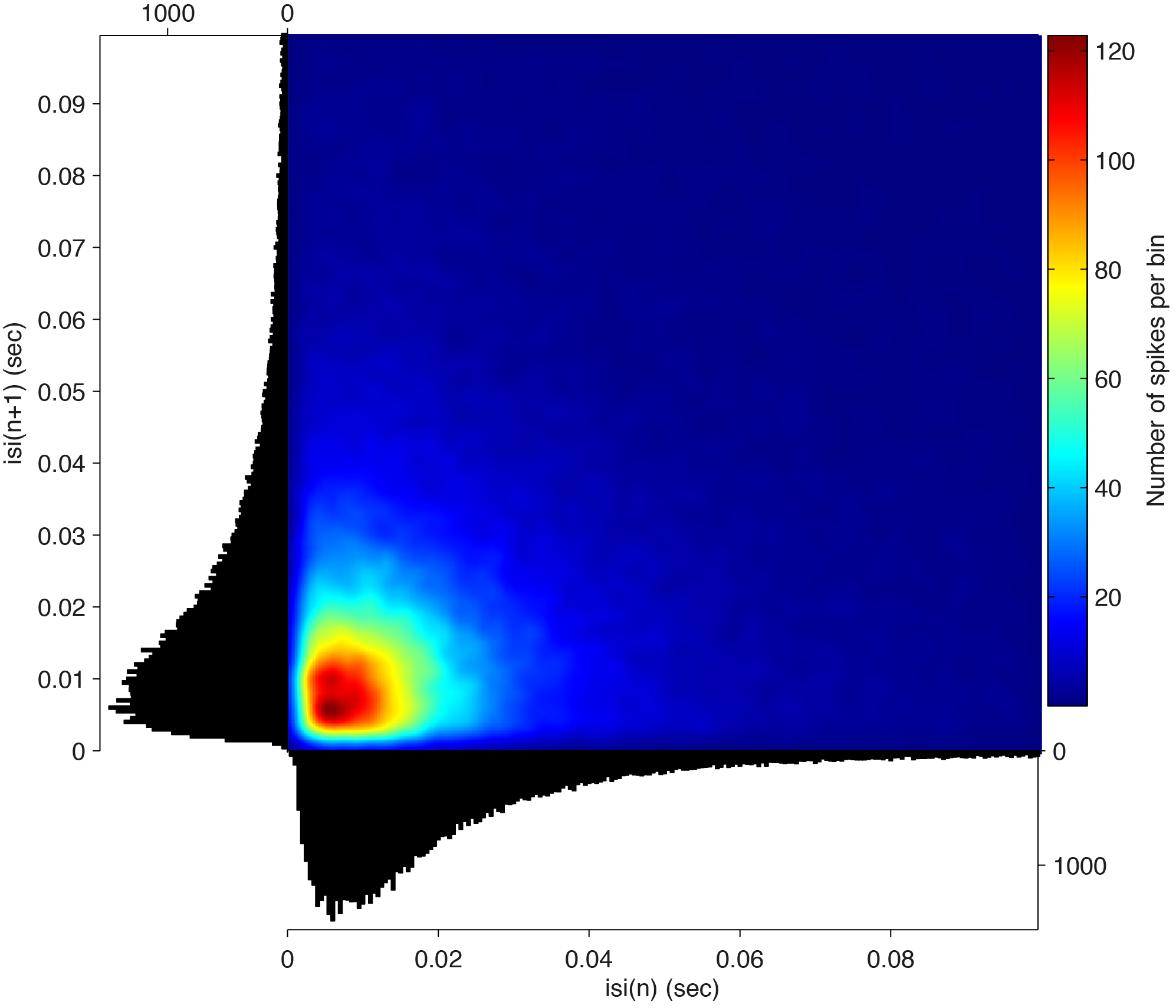
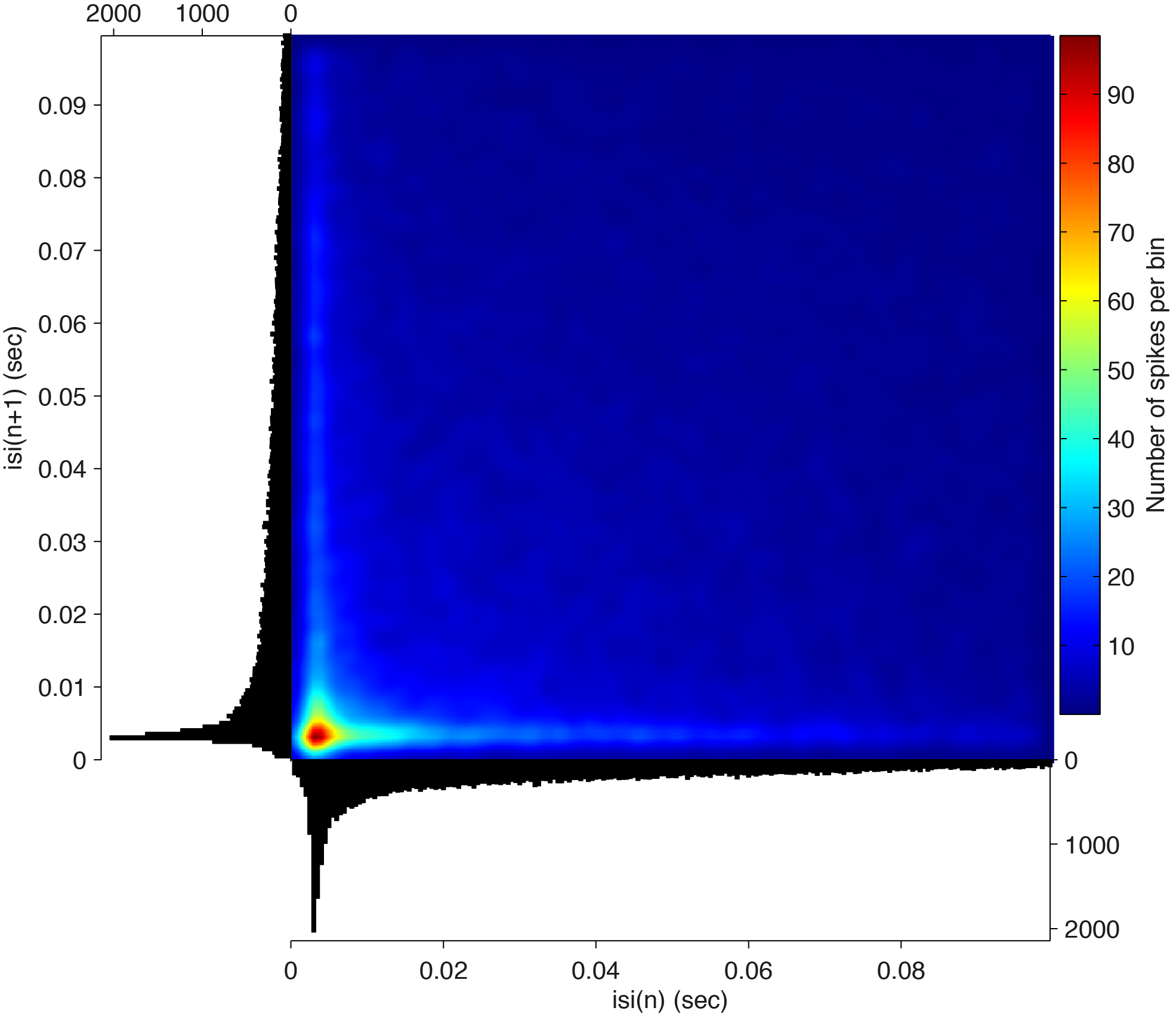
The field isih.isi contains the isi per spike (w.r.t the previous spike) and contains NaNs at the beginning of the trials. The field isih.avg contains the average isi histogram per unit, and isih.coeffvar the computed parameter summarizing the statistics of the isi histogram (e.g., see Shinomoto et al., 2009) .We then plot the isi histogram (which can be plotted alone using ft_spike_plot_isi) together with the isi (Poincare) return plot, which plots the current isi(n) against the next isi(n+1), thereby giving insight into the second order statistics of the isi distribution:
for k = [1 2] % only do for the single-units
cfg = [];
cfg.spikechannel = isih.label{k};
cfg.interpolate = 5; % interpolate at 5 times the original density
cfg.window = 'gausswin'; % use a gaussian window to smooth
cfg.winlen = 0.004; % the window by which we smooth has size 4 by 4 ms
cfg.colormap = jet(300); % colormap
cfg.scatter = 'no'; % do not plot the individual isis per spike as scatters
figure, ft_spike_plot_isireturn(cfg,isih)
end
This gives two figures, one with a longer refractory period (the narrow spiking cell; top), and one with a bursting pattern (the broad spiking cell; bottom)
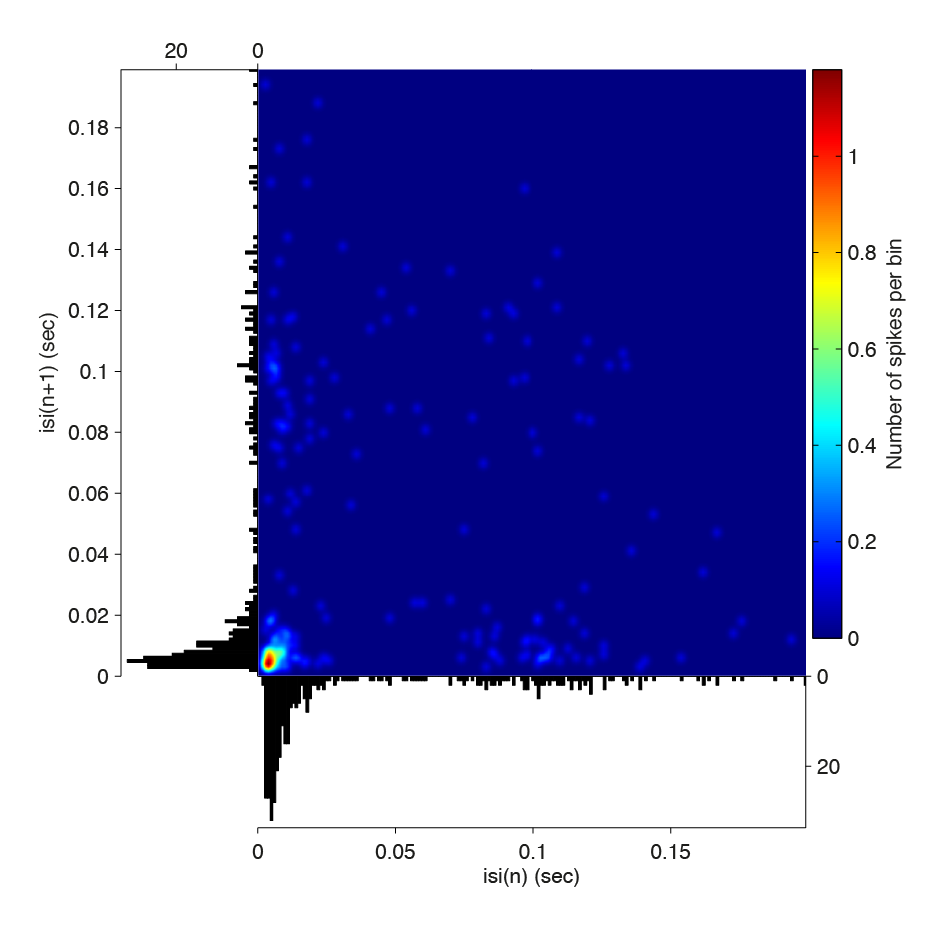
We also read in an additional dataset consisting of an M-clust .t file, that can be found here
% read in the .t file
filename = 'tt6_7.t'
cfg = [];
cfg.dataset = filename;
spike2 = ft_read_spike(cfg.dataset)
% convert timestamps to seconds
cfg = [];
cfg.trl = [0 max(spike2.timestamp{1})+1 0];
cfg.timestampspersecond = 10^6;
spike2Trial = ft_spike_maketrials(cfg,spike2);
% run the isi histogram
cfg = [];
cfg.bins = [0:0.001:0.2];
isih = ft_spike_isi(cfg,spike2Trial);
% plot the isi histogram with the Poincare return map
cfg = [];
cfg.interpolate = 5;
cfg.window = 'gausswin';
cfg.winlen = 0.005;
cfg.scatter = 'no';
cfg.colormap = jet(300);
figure, ft_spike_plot_isireturn(cfg,isih)
This plot shows that after a burst, either a new burst follows, or a long waiting period on the order of a theta cycle (100 ms).
Computing spike densities and peri-stimulus time histograms (PSTHs)
Both spike-density functions and peri-stimulus time histograms are methods to compute the average firing rate at selected time points around event triggers. This is an important step to understand how neurons react to changes in external variables. For computing the PSTH, use the function ft_spike_psth.
Running
cfg = [];
cfg.binsize = 0.1; % if cfgPsth.binsize = 'scott' or 'sqrt', we estimate the optimal bin size from the data itself
cfg.outputunit = 'rate'; % give as an output the firing rate
cfg.latency = [-1 3]; % between -1 and 3 sec.
cfg.vartriallen = 'yes'; % variable trial lengths are accepted
cfg.keeptrials = 'yes'; % keep the psth per trial in the output
psth = ft_spike_psth(cfg,spikeTrials);
gives us the output
psth =
avg: [2x40 double]
var: [2x40 double]
dof: [2x40 double]
fsample: 10
time: [1x40 double]
label: {'sig002a_wf' 'sig003a_wf'}
trial: [600x2x40 double]
dimord: 'rpt_chan_time'
sampleinfo: [600x2 double]
cfg: [1x1 struct]
The PSTH structure is a so called ‘timelock’ data structure (ft_datatype_timelock, and can as such be used in all functions taking timelock structures as an input. The field psth.avg contains the average firing rates per bin per unit, and psth.trial contains the average firing rate per trial per unit per time-bin. It is also possible (but less computationally efficient) to enter the binary spike trains that are stored in a continuous raw format. The data is then automatically converted to a spike structure within ft_spike_psth.
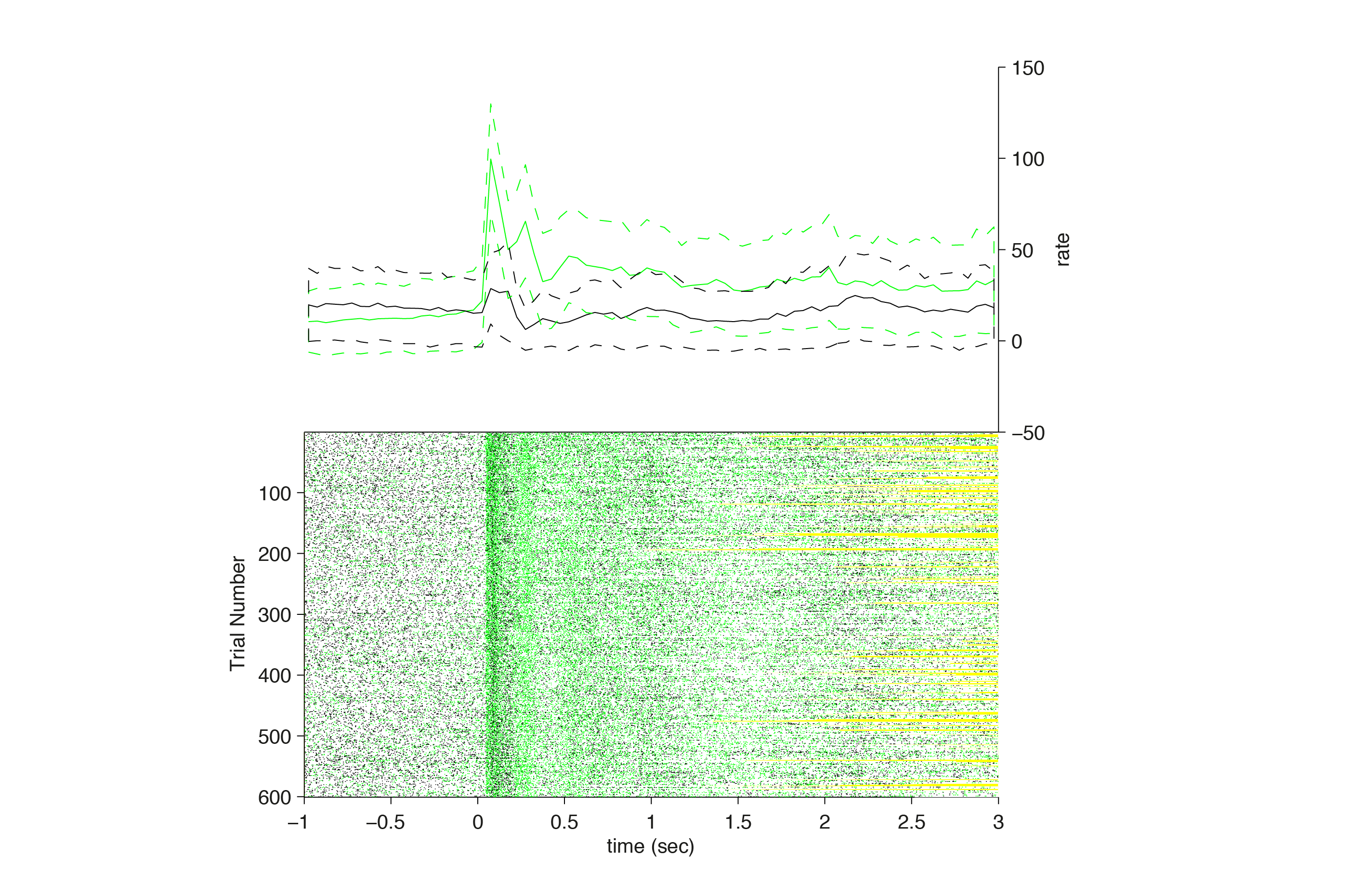
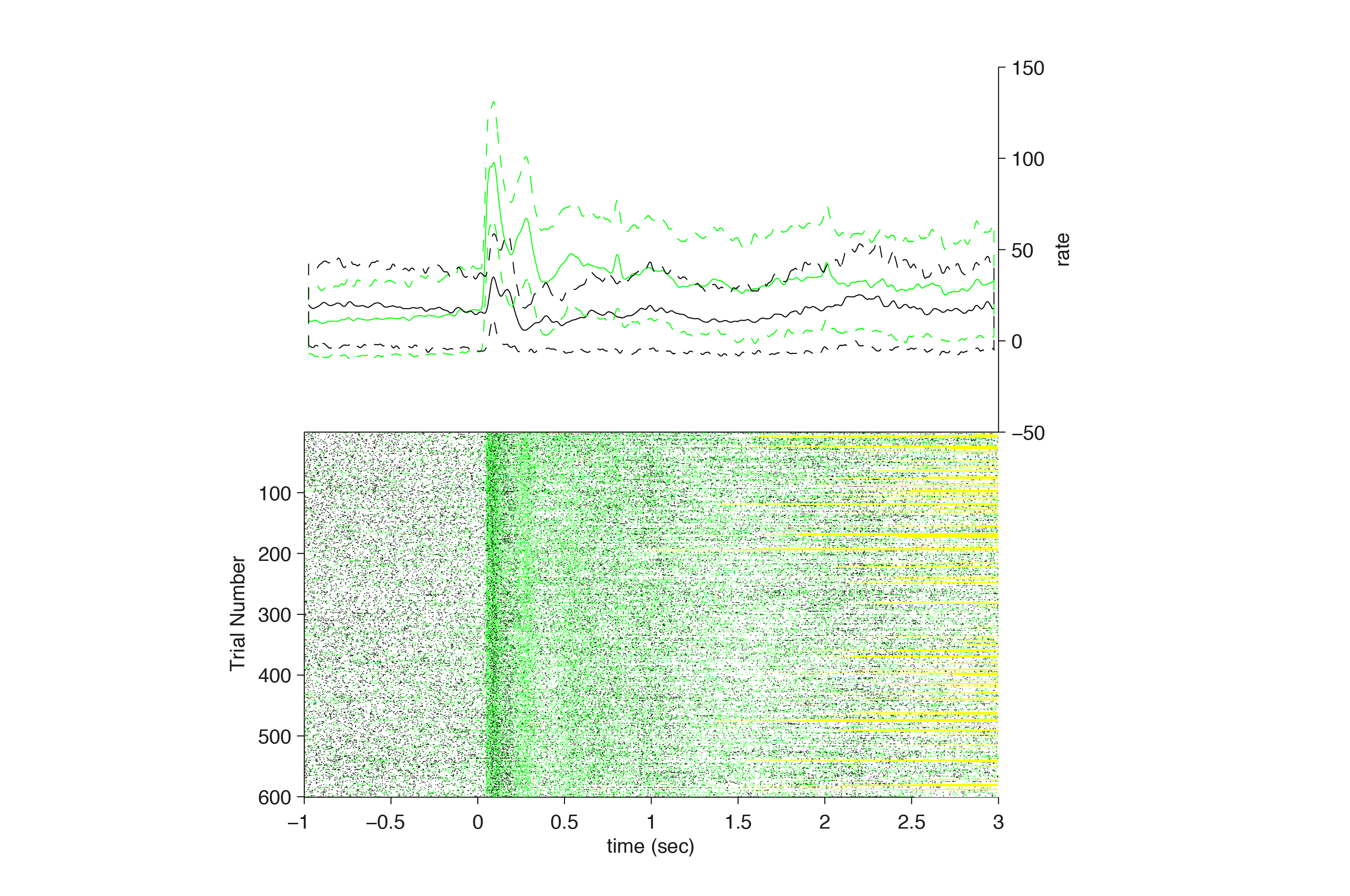
A raster plot with psth is obtained by running
cfg = [];
cfg.binsize = [0.05];
cfg.latency = [-1 3];
psth = ft_spike_psth(cfg,spikeTrials);
cfg = [];
cfg.topplotfunc = 'line'; % plot as a line
cfg.spikechannel = spikeTrials.label([1 2]);
cfg.latency = [-1 3];
cfg.errorbars = 'std'; % plot with the standard deviation
cfg.interactive = 'no'; % toggle off interactive mode
figure, ft_spike_plot_raster(cfg,spikeTrials, psth)
The yellow lines in the raster plot indicate the trial borders. Configuration options are available to control spike length and width, and size of the raster relative to the summarizing PSTH / spike density data. Also, multiple neurons are plotted with different colors. This can also be used to plot multiple conditions at the same time.
We then run spike-density functions on the spike trains, to obtain spike density with rasters. The advantage of the spike-density function is that an estimate of the instantaneous firing rate or expected spike count can be obtained for every time-point, instead of larger bins (as with the PSTH).
cfg = [];
cfg.latency = [-1 3];
cfg.timwin = [-0.025 0.025];
cfg.fsample = 1000; % sample at 1000 hz
sdf = ft_spikedensity(cfg,spikeTrials);
cfg = [];
cfg.topplotfunc = 'line'; % plot as a line plot
cfg.spikechannel = spikeTrials.label([1 2]); % can also select one unit here
cfg.latency = [-1 3];
cfg.errorbars = 'std'; % plot with standard deviation
cfg.interactive = 'no'; % toggle off interactive mode
figure, ft_spike_plot_raster(cfg,spikeTrials, sdf)
The output from ft_spikedensity is again a timelock structure. A second output can be obtained from ft_spikedensity, containing the estimated spike densities per trial in a continuous raw data structure. To this end, do:
cfg = [];
cfg.latency = [-1 3];
cfg.timwin = [-0.1 0.1];
cfg.fsample = 1000; % sample at 1000 hz
[sdf, sdfdata] = ft_spikedensity(cfg,spikeTrials);
Now, sdfdata is a continuous raw structure with the following content:
sdfdata =
trial: {1x600 cell}
time: {1x600 cell}
fsample: 1000
label: {'sig002a_wf' 'sig003a_wf'}
hdr: [1x1 struct]
cfg: [1x1 struct]
For example,
sdfdata.trial{1}(:,3000:3005)
69.9088 68.6629 68.5491 68.4371 68.3268 67.1327
12.2671 12.2494 12.2315 12.2135 12.1954 12.1772
Computing average firing rates and noise correlations
The average firing rates for a certain period are computed by
cfg = [];
cfg.latency = [0.3 max(spikeTrials.trialtime(:))]; % sustained response period
cfg.keeptrials = 'yes';
rate = ft_spike_rate(cfg,spikeTrials);
The output rate is a timelock structure with the content:
rate =
avg: [2x1 double]
var: [2x1 double]
dof: [2x1 double]
label: {'sig002a_wf' 'sig003a_wf'}
dimord: 'rpt_chan_time'
time: 2.6617
trial: [600x2 double]
cfg: [1x1 struct]
An important question in neurophysiology is whether neurons are capable of transmitting information independent from each other, or whether neurons have shared trial-by-trial fluctuations (called ‘noise correlations’) in their firing rate (given an identical stimulus) that diminish the coding capacity of the population (e.g., see Ecker et al., 2010).
One can compute noise correlations between units by doing
[R,P] = corrcoef(rate.trial)
R = % Pearson's R
1.0000 0.0988
0.0988 1.0000
P = % probability
1.0000 0.0155
0.0155 1.0000
Computing cross-correlations between spike trains
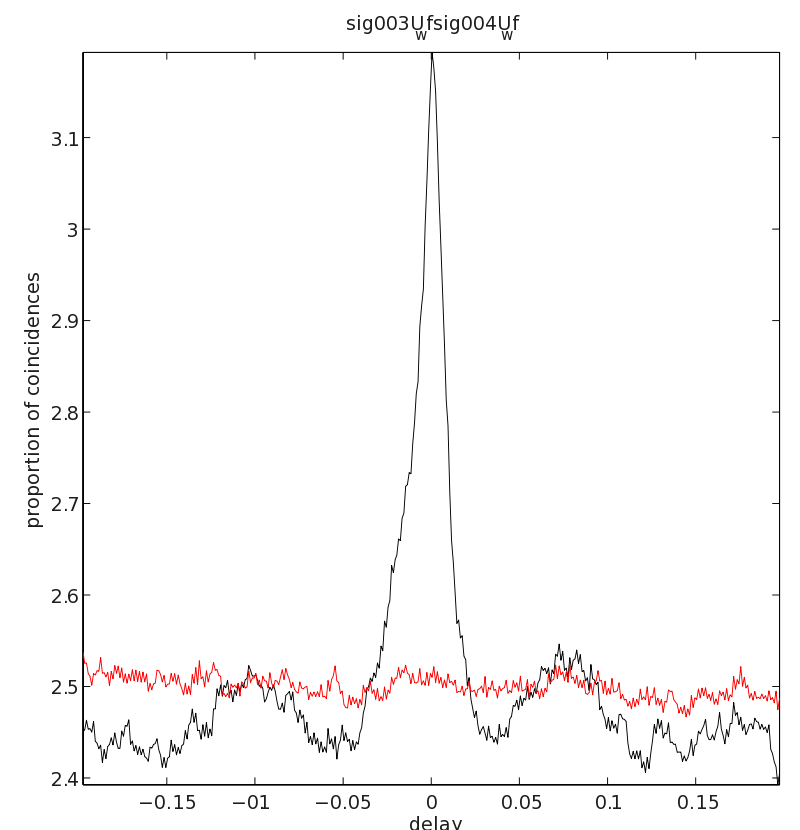
Auto- and cross-correlations between spike trains are computed using ft_spike_xcorr. The cross-correlogram is one of the classic techniques to show rhythmic synchronization between different neurons (e.g., see Gray et al., 1989) but also to identify synaptic connections between recorded neurons (e.g., see Bartho et al., 2004). The auto-correlogram typically offers a more sensitive measure of the degree to which a single neuronal source displays rhythmic firing than the ISI distribution, especially if firing rates are high. For this analysis we select the unsorted multi-units from the same data-set, as they give more reliable cross-correlations. The observed cross-correlogram should always be compared against a cross-correlogram obtained by shuffling the trials. Cross-correlations between neurons can either arise because of common, time-locked fluctuations in the firing rate (Brody et al., 1999). These correlations are invariant to a change in the order of trials. The shuffling of trials in ft_spike_xcorr always pertains to two subsequent trials, in order to avoid an influence of slow changes in the firing rate across trials. We refer to this cross-correlogram that is obtained under a permutation of subsequent trials as the ‘shift-predictor’ cross-correlogram. If the observed features of the cross-correlogram that are not present in the shift-predictor cross-correlogram, then this indicates that they arise because of induced synchronous activity. Note that for the shift-predictor, it is required that the trials cover the full latency window that is specified by cfg.latency. For example, if the first trial has a duration of 3 sec. and the second of 2 sec., we can only compute the contribution to the shift-predictor based on the spikes from the first 2 seconds. Hence, cfg.vartriallen must be specified to ‘no’.
We run the following
% read in the data, select the channels and define the trials
spike = ft_read_spike('p029_sort_final_01.nex');
cfg = [];
cfg.spikechannel = {'sig001U_wf', 'sig002U_wf', 'sig003U_wf', 'sig004U_wf'}; % select only the MUA
spike = ft_spike_select(cfg, spike);
cfg = [];
cfg.dataset = 'p029_sort_final_01.nex';
cfg.trialfun = 'trialfun_stimon';
cfg = ft_definetrial(cfg);
cfg.timestampspersecond = spike.hdr.FileHeader.Frequency; % 40000
spikeTrials = ft_spike_maketrials(cfg,spike);
and then compute the cross-correlogram (and the shift-predictor cross-correlogram) by
cfg = [];
cfg.maxlag = 0.2; % maximum 200 ms
cfg.binsize = 0.001; % bins of 1 ms
cfg.outputunit = 'proportion'; % make unit area
cfg.latency = [-2.5 0];
cfg.vartriallen = 'no'; % do not allow variable trial lengths
cfg.method = 'xcorr'; % compute the normal cross-correlogram
Xc = ft_spike_xcorr(cfg,spikeTrials);
% compute the shuffled correlogram
cfg.method = 'shiftpredictor'; % compute the shift predictor
Xshuff = ft_spike_xcorr(cfg,spikeTrials);
The output Xc is a structure with the following content
Xc =
xcorr: [4x4x400 double]
time: [1x400 double]
dimord: 'chan_chan_time'
label: {'sig001U_wf' 'sig002U_wf' 'sig003U_wf' 'sig004U_wf'}
cfg: [1x1 struct]
For every channel combination (j,k) the element Xc.corr(j,k,:) contains the cross-correlogram.
For example, the computed cross-correlogram reveals strong zero-lag and alpha-band synchronization in the pre-stimulus period:
iCmb = 3;
jCmb = 4;
figure
xcSmoothed = conv(squeeze(Xc.xcorr(iCmb,jCmb,:)),ones(1,5)./5,'same'); % do some smoothing
hd = plot(Xc.time(3:end-2),xcSmoothed(3:end-2),'k'); % leave out borders (because of smoothing)
hold on
xcSmoothed = conv(squeeze(Xshuff.shiftpredictor(iCmb,jCmb,:)),ones(1,5)./5,'same');
plot(Xc.time(3:end-2),xcSmoothed(3:end-2),'r')
hold on
xlabel('delay')
ylabel('proportion of coincidences')
title([Xc.label{iCmb} Xc.label{jCmb}])
axis tight
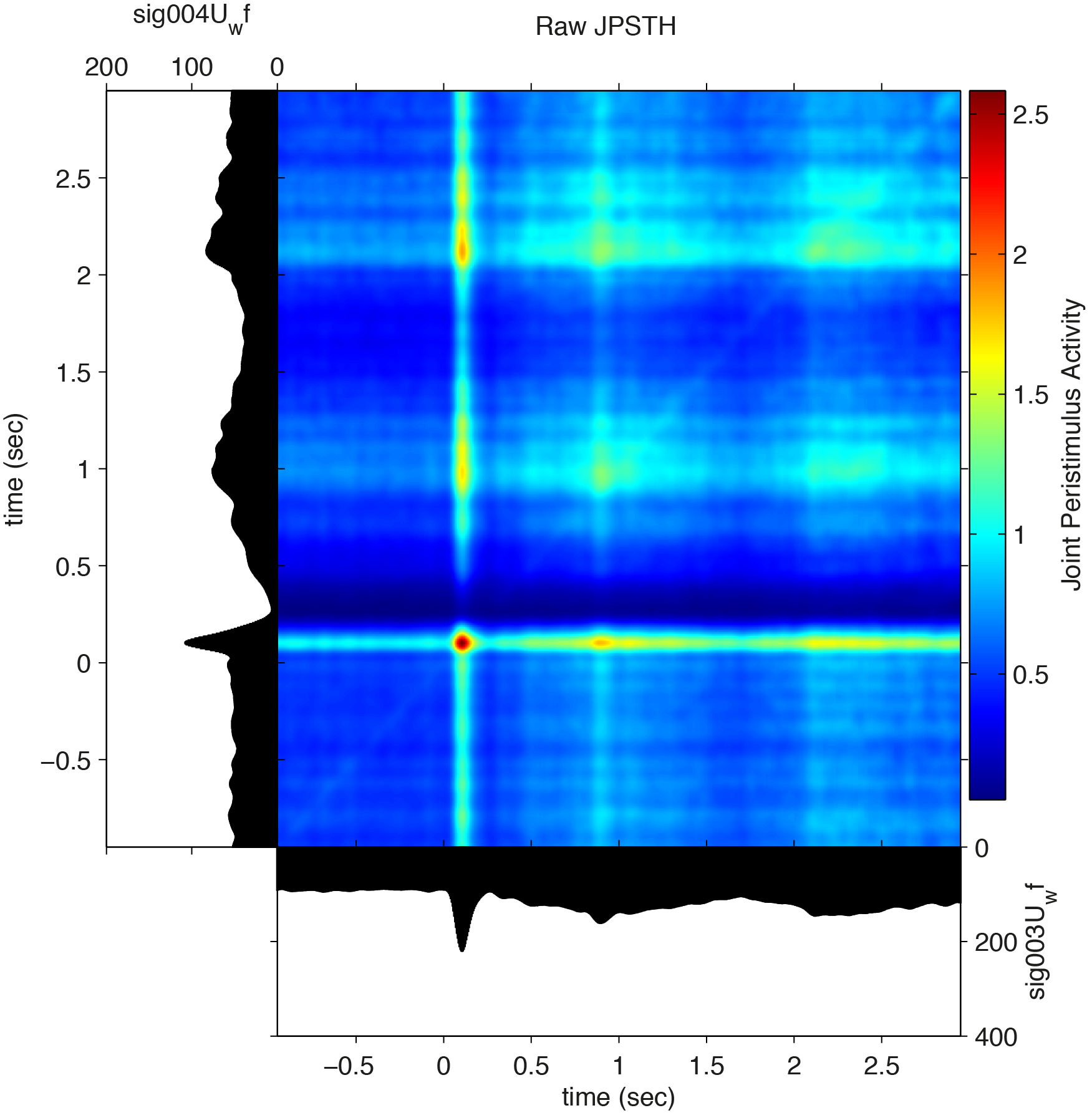
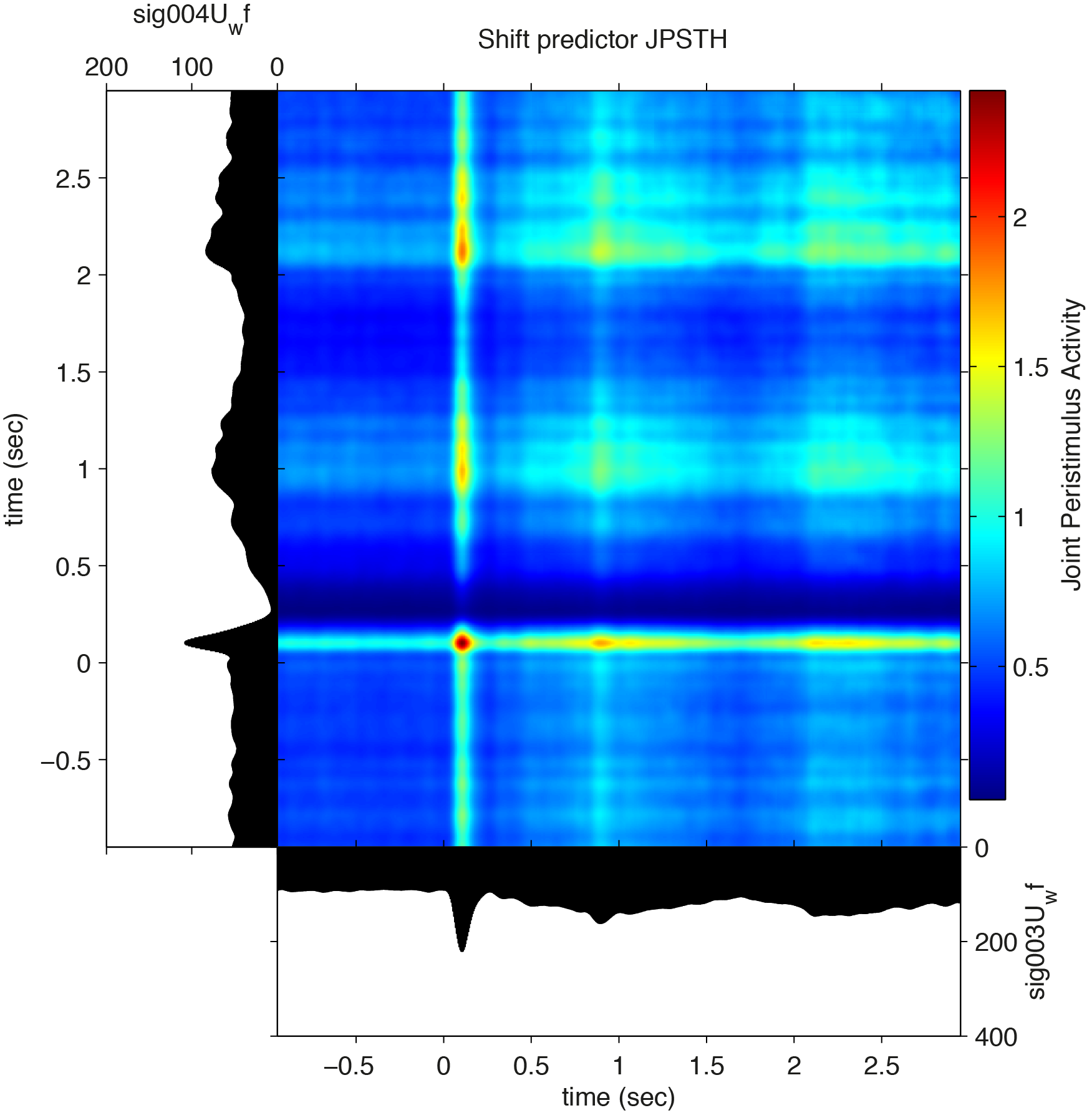
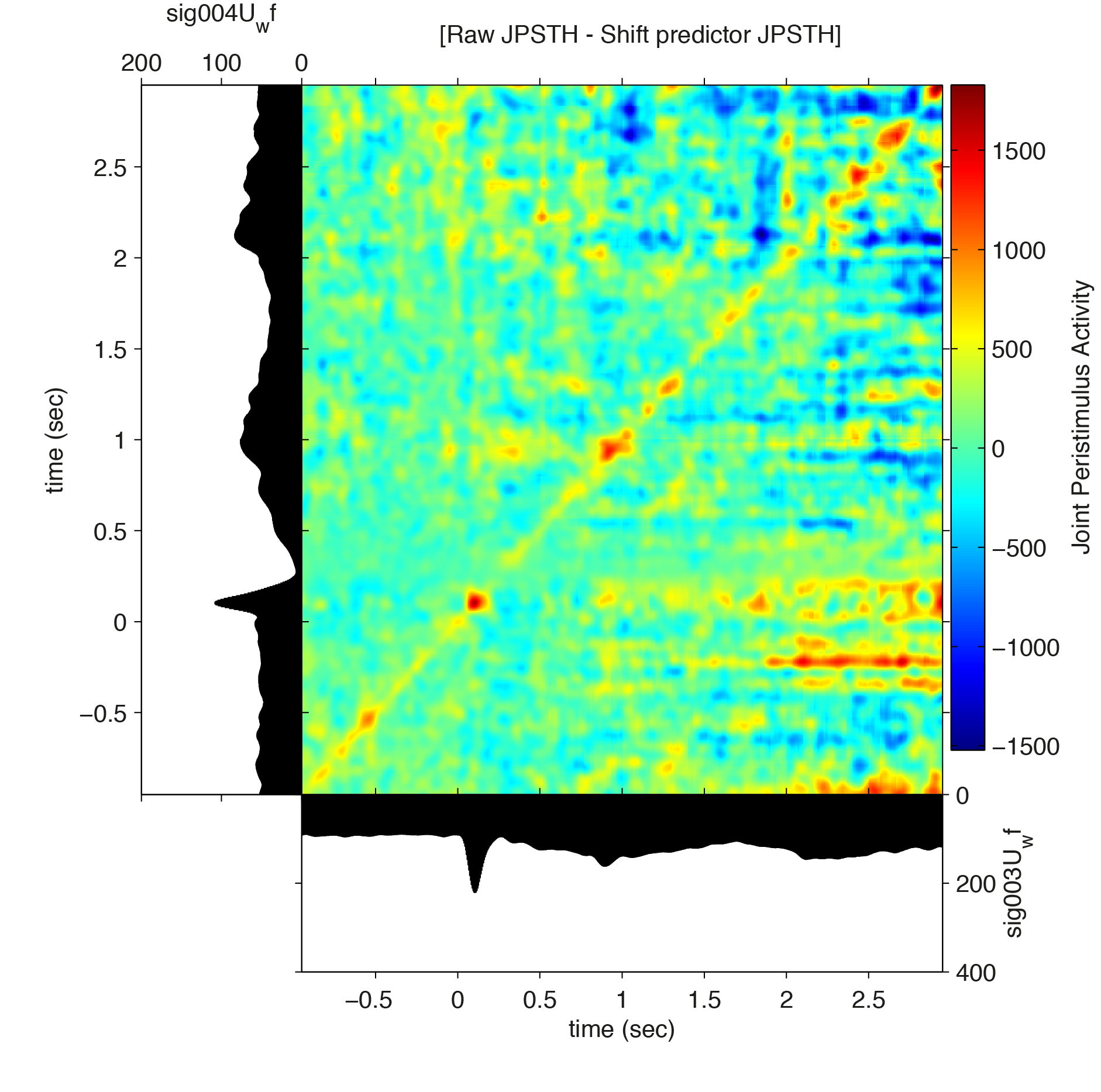
The joint peri stimulus time histogram
Cross-correlations are computed over the complete trial period. To gain insight into the temporal evolution of spike-spike correlations, the JPSTH tool can be used. We compute the JPSTH using ft_spike_jpsth and visualize it using ft_spike_plot_jpsth.
% compute the spike densities
cfg = [];
cfg.latency = [-1 3];
cfg.timwin = [-0.025 0.025];
cfg.fsample = 200;
[sdf] = ft_spikedensity(cfg,spikeTrials);
% compute the joint psth
cfg = [];
cfg.normalization = 'no';
cfg.channelcmb = spikeTrials.label(3:4);
cfg.method = 'jpsth';
jpsth = ft_spike_jpsth(cfg,sdf);
cfg.method = 'shiftpredictor';
jpsthShuff = ft_spike_jpsth(cfg,sdf);
% subtract the predictor
jpsthSubtr = jpsth;
jpsthSubtr.jpsth = jpsth.jpsth-jpsthShuff.shiftpredictor;
We then plot the JPSTH using ft_spike_plot_jpsth
cfg = [];
figure
ft_spike_plot_jpsth(cfg,jpsth)
figure, ft_spike_plot_jpsth(cfg,jpsthShuff)
figure, ft_spike_plot_jpsth(cfg,jpsthSubtr)
giving the normalized jpsth, the shuffle corrected normalized jpsth, and the difference between the two, revealing an increase in synchronization between spike trains that is not due to evoked, joint fluctuations in the firing rate.
Summary
We have shown how to perform several common spike train analyses. As the outputs from many functions are standard FieldTrip functions (e.g., the output from ft_spikedensity), the powerful statistical methods available in FieldTrip can be readily applied on them. Also not discussed was the joint analysis of LFP and spike data. but this is dealt with in the spikefield tutorial.