This page is still under construction

SQUIDs versus OPMs

Introduction

Traditional MEG systems use superconducting quantum interference devices (SQUIDs), which require expensive cryogenic cooling with liquid helium and involve placing the sensors 1.5-2 cm from the scalp. Optically pumped magnetometers (OPMs), a new generation of MEG, eliminate the need for cryogenic cooling, allowing sensors to be placed closer to the scalp. OPMs are small individual sensors that allow the researcher to choose where to place them over the head. These sensors are held in place by 3D-printed helmets, which can be customized for each subject.

Even though both SQUID and OPM system detect the brain’s magnetic fields, their data analysis steps differ a bit. In this tutorial we explore the differences in preprocessing and coregistration between the two systems.

OPMs are flexible in their placement allowing for new recording strategies. These new recording strategies lead to new data analysis strategies. For example, in this tutorial we use a small number of OPMs (32 sensors) and do sequential recordings in which we position them over different places over the scalp.

OPMs are magnetometers, as their name suggests. Magnetometers are more sensitive to environmental noise than gradiometers, which most SQUID systems have. Several data analysis algorithms to remove environmental noise have been proposed (see Seymour et al (2022) for more details). In this tutorial, we apply homogeneous field correction (HFC). HFC works better with a large number of sensors.

Unlike SQUID systems, which have standard coregistration strategies, OPMs don’t have a single coregistration standard. In this tutorial, we coregister the OPMs with the MRI using an optical 3D scanner which captures the participant’s facial features along with the OPM helmet (Zetter et al., 2019).

This tutorial combines the FieldTrip tutorials on preprocessing of Optically Pumped Magnetometer (OPM) data and coregistration of Optically Pumped Magnetometer (OPM) data. It does not cover follow-up analyses (like source reconstruction) which in principle should not differ from the SQUID follow-up analyses, or alternative coregistration methods which are covered in the tutorial on coregistration of Optically Pumped Magnetometer (OPM) data.

Background

In this tutorial we will use recordings made with 32 OPM sensors placed in an adult-sized “smart” helmet with a total of 144 slots. This helmet is called “smart” as each slot allows the sensor to slide in until it touches the head surface, regardless of the head size and shape. To limit head movements we mounted the helmet on a wooden plate located behind the subject chair.

To acquire a measurement for each of the 144 helmet slots, we divided the experiment into six runs. To maintain the participant’s head fixed between runs, we kept 9 sensors around the participant’s head fixed for all the runs. The remaining 23 sensors were moved to different helmet slots in each run to cover the whole scalp as homogeneously as possible.

The dataset used in this tutorial

The data for this tutorial was recorded with a 32-sensor FieldLine HEDscan v3 system with a so-called smart helmet. Each OPM sensor has one channel that measures the normal component of the magnetic field.

We perform a left median nerve stimulation experiment on a single participant in both the SQUID and the OPM system. We expect to find a dipole 20 ms post-stimulation in the right primary somatosensory area (Andersen & Dalal, 2021; Buchner et al., 1994).

The dataset can be downloaded from our download server.

Procedure

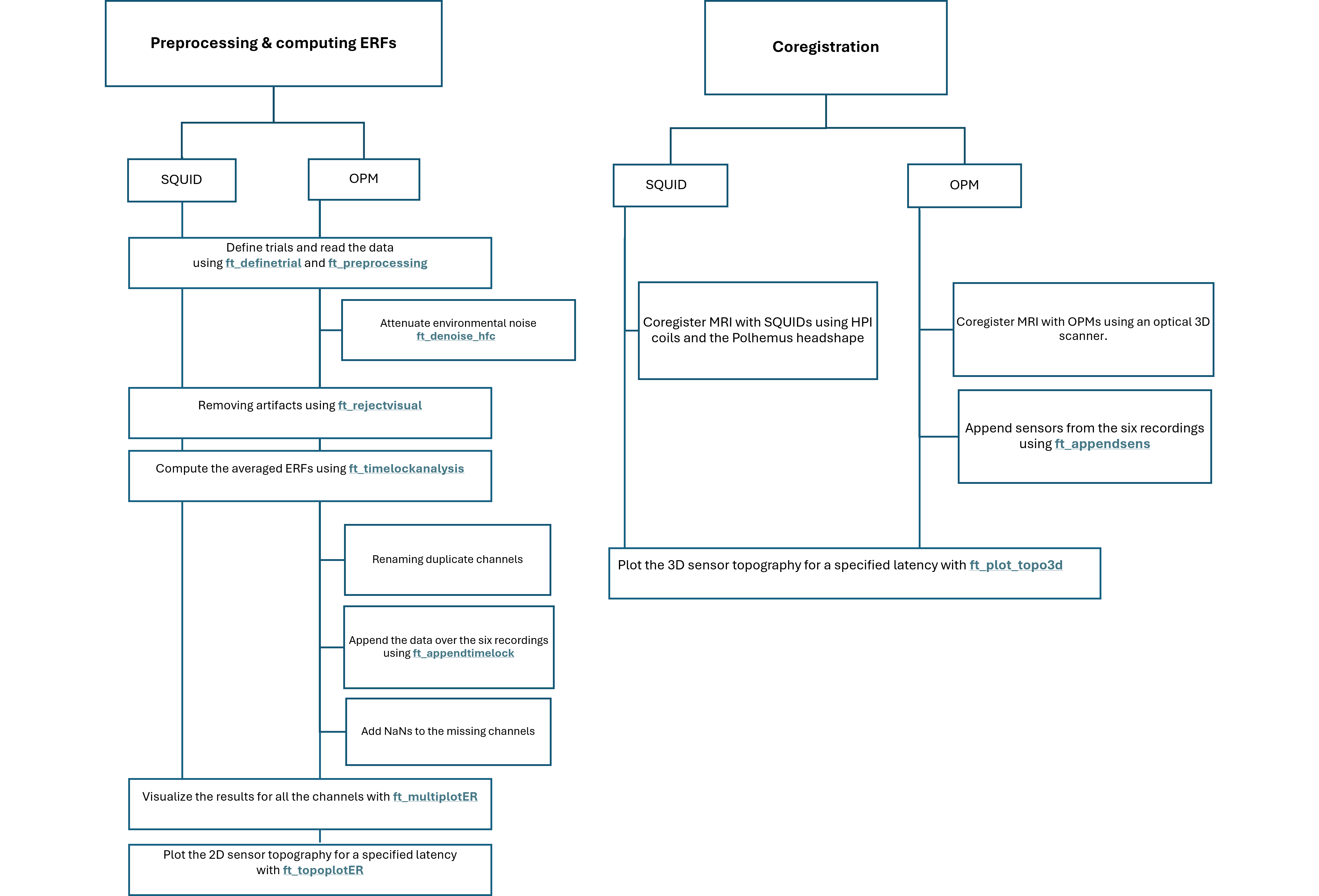
In this tutorial for the SQUIDs we will take the following steps:

For the OPMs we will take the following steps:

Preprocessing & computing ERFs

SQUID

We begin by loading the SQUID data and defining trials. We select trials in which left median nerve stimulation occurred (trigger code = 1). In the experiment, the inter-trial interval ranged from 800-1200 ms, so it makes sense to select a 200 ms prestimulus and 400 ms poststimulus window.

%% Preprocessing & trial definition

cfg                     = [];
cfg.dataset             = 'sub-01_ses-01_task-MedianNervesStim_squid.ds'; % add the whole path to your meg file
cfg.trialdef.eventtype  = 'UPPT001';
cfg.trialdef.eventvalue = [1]; 
cfg.trialdef.prestim    = 0.2; 
cfg.trialdef.poststim   = 0.4;
cfg                     = ft_definetrial(cfg);

cfg.demean         = 'yes'; % apply baseline correction
cfg.baselinewindow = [-Inf 0]; 
cfg.channel        = 'MEG';
cfg.continuous     = 'yes';
data_squid         = ft_preprocessing(cfg);

save data_squid data_squid

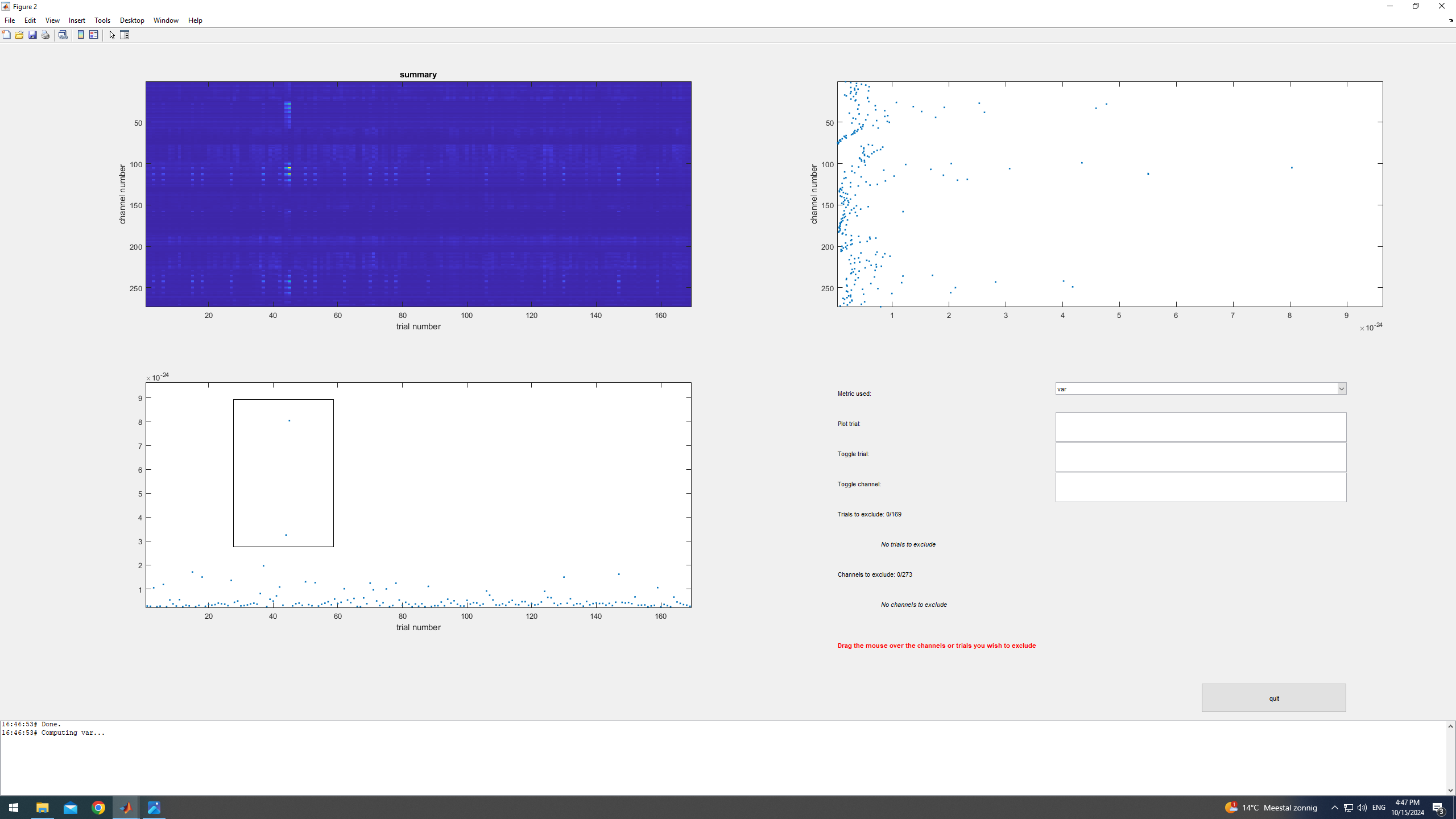
The summary method in ft_rejectvisual allows to manually remove trials and/or channels that have high variance.

%% Removing artifacts manually

load data_squid data_squid

cfg              = [];
cfg.method       = 'summary';
data_squid_clean = ft_rejectvisual(cfg, data_squid);

save data_squid_clean data_squid_clean

We start by removing trials that have higher variance (bottom-left plot). Based on our data, a reasonable threshold to choose is 8e-25 Tesla-squared. Next, we assess the channel variance (top-right plot). Removing trials with high variance resulted in reducing the channel variance too, so no need to reject any channels.

We then calculate the ERFs:

%% Computing ERFs

load data_squid_clean data_squid_clean

cfg       = [];
avg_squid = ft_timelockanalysis(cfg, data_squid_clean);

save avg_squid avg_squid

We plot the activity from all the sensors.

%% Plotting ERFs

load avg_squid avg_squid

cfg = [];
cfg.layout = 'CTF275_helmet';
ft_multiplotER(cfg, avg_squid); % use interactively

Interactive mode: Explore the event-related potential by dragging boxes around (groups of) sensors and time points in the ‘multiplot’ and the resulting ‘singleplots’ and ‘topoplots’. Can you find the time window that the dipolar activity at the right primary somatosensory area appears?

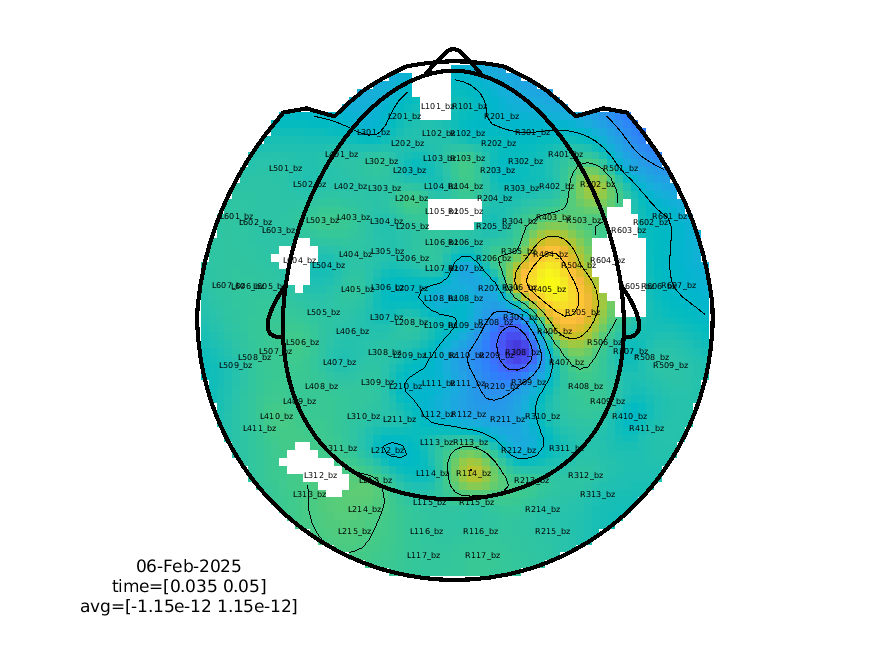
We can also plot this dipolar pattern with ft_topoplotER.

%% Plotting the topography

cfg = [];
cfg.xlim = [0.035 0.050];
cfg.layout = 'CTF275_helmet';
ft_topoplotER(cfg, avg_squid); 

print -dpng cuttingeegx_topo_squid.png

OPM

%% Preprocessing & trial definition

f = dir('*.fif'); % add the whole path to your .fif files
f = struct2cell(f);

 for i = 1:6  % 6 experimental runs  

    cfg                     = [];
    cfg.dataset             = fullfile(f{2,i},f{1,i});
    cfg.trialdef.eventtype  = 'ai61';
    cfg.trialdef.eventvalue = [1];
    cfg.trialdef.prestim    = 0.2; 
    cfg.trialdef.poststim   = 0.4;
    cfg                     = ft_definetrial(cfg);
    
    cfg.demean         = 'yes'; % apply baseline correction
    cfg.baselinewindow = [-Inf 0];
    cfg.channel        = {'all', '-ai61'};
    data_opm(i)        = ft_preprocessing(cfg);

 end

save data_opm data_opm

OPM are magnetometers which are more sensitive to the environmental noise than the SQUID gradiometers. To remove some of the environmental noise, several algorithmic denoising techniques have been proposed (Seymour et al., 2022). In this tutorial we will apply homogeneous field correction (HFC) (Tierney et al., 2021).

%% HFC

load data_opm data_opm

for i=1:6
    data_opm_nohdr(i) = rmfield(data_opm(i), 'hdr'); % it is needed so that ft_denoise_hfc() works

    cfg               = [];
    data_opm_hfc(i)   = ft_denoise_hfc(cfg, data_opm_nohdr(i));
end

save data_opm_hfc data_opm_hfc

We will now manually remove trials with high variance.

%% Removing artifacts manually

load data_opm_hfc data_opm_hfc

for i=1:6
    cfg                   = [];
    cfg.method            = 'summary';
    data_opm_hfc_clean(i) = ft_rejectvisual(cfg, data_opm_hfc(i));
end

save data_opm_hfc_clean data_opm_hfc_clean

For the SQUID-based recordings, we removed trials with variance above the threshold of 8e-25 Tesla-squared. Is it possible to use the same threshold for the OPMs? If not, why and does this affect the quality of the OPM signal? Remember that (i) OPMs are magnetometers, and (ii) they are placed closer to the scalp than the SQUIDs.

%% Computing ERFs

load data_opm_hfc_clean data_opm_hfc_clean

for i=1:6
    cfg        = [];
    avg_opm(i) = ft_timelockanalysis(cfg, data_opm_hfc_clean(i));
end 

save avg_opm avg_opm

Before concatenating the six runs, we need to rename duplicate channels. Duplicates arise for three reasons: (i) 9 sensors were fixed across all runs, (ii) some sensors in the sixth run were in the same slot as the fifth run due to limited remaining free slots, and (iii) errors by the researcher placing a sensor in same slot between runs. During the recording an excel sheet was used to keep track in which slot each sensor was placed. We use that information to rename the channels.

%% Renaming channels

load avg_opm avg_opm

avg_opm_rename = avg_opm;

% 9 sensors were fixed across all runs. Note L101 was not working so we do not need to rename it. 
for k = 2:6
    index = find(ismember(avg_opm(k).label, {'R101_bz', 'L108_bz','R503_bz','L503_bz','L507_bz','R507_bz','R212_bz','L212_bz'})); % 2 in the back, 2 right, 2 left, 1 front, 1 top
    for i = 1:length(index)
        avg_opm_rename(k).label{index(i)} = strcat(avg_opm(k).label{index(i)}, '_', num2str(k));
    end
end

% Some sensors in the sixth run were in the same slot as the fifth run
for k = 6 % 6th run
    index = find(ismember(avg_opm_rename(k).label, {'R114_bz', 'L504_bz'})); % rename 'R114_bz', 'L504_bz'
    for i = 1:length(index)
        avg_opm_rename(k).label{index(i)} = strcat(avg_opm_rename(k).label{index(i)}, '_', num2str(k));
    end
end

% Researchers' errors
for k = 2 % 2nd run 
    index = find(ismember(avg_opm_rename(k).label, {'L214_bz'})); % rename 'L214_bz'
    for i = 1:length(index)
        avg_opm_rename(k).label{index(i)} = strcat(avg_opm_rename(k).label{index(i)}, '_', num2str(k));
    end
end

for k = 5 % 5th run
    index = find(ismember(avg_opm_rename(k).label, {'R504_bz', 'L504_bz'})); % rename 'R504_bz', 'L504_bz'
    for i = 1:length(index)
        avg_opm_rename(k).label{index(i)} = strcat(avg_opm_rename(k).label{index(i)}, '_', num2str(k));
    end
end

save avg_opm_rename avg_opm_rename

We concatenate ERFs across the six runs to simulate a single experiment with 144 sensors (note: there are some missing sensors, so in the end we do not have 144 sensors).

%% Append the ERFs over the six runs

load avg_opm_rename avg_opm_rename

cfg           = [];
cfg.appenddim = 'chan';
append_opm    = ft_appendtimelock(cfg, avg_opm_rename(1), avg_opm_rename(2), avg_opm_rename(3), avg_opm_rename(4), avg_opm_rename(5), avg_opm_rename(6));

% renaming the appended averages to "avg" as this is the default in
% FieldTrip
append_opm.avg = append_opm.trial;
append_opm     = rmfield(append_opm, 'trial');

save append_opm append_opm

There are some missing sensors. To avoid interpolation or extrapolation artifacts in the topography, we can add NaNs for the missing sensors and then tell to ft_topoplotER to exclude those using the 'cfg.interpolatenan = no' option.

%% Add NaNs to the missing channels

load fieldlinebeta2bz_helmet.mat 
missing = setdiff(layout.label, append_opm.label); 

% missing =
% 
%   8×1 cell array
% 
%     {'L101_bz'}
%     {'L105_bz'}
%     {'L312_bz'}
%     {'L604_bz'}
%     {'R105_bz'}
%     {'R603_bz'}
%     {'R604_bz'}
%     {'R605_bz'}

% make a copy of the original timelock structure, remove two fields that we don't care about
append_opm_nan = rmfield(append_opm, {'dof', 'var'});

% add NaNs to the extra slots from the helmet that are missing 
append_opm_nan.label = cat(1, append_opm_nan.label(:), missing(:));
append_opm_nan.avg   = cat(1, append_opm_nan.avg, nan(numel(missing), numel(append_opm_nan.time)));

save append_opm_nan append_opm_nan

%% Plotting ERFs

load append_opm_nan append_opm_nan
 
cfg            = [];
cfg.layout     = 'fieldlinebeta2bz_helmet';
cfg.showlabels = 'yes';
cfg.ylim       = 'maxabs';
ft_multiplotER(cfg, append_opm_nan);

%% Plotting the topography

cfg                = [];
cfg.xlim           = [0.035 0.050];
cfg.layout         = 'fieldlinebeta2bz_helmet';
cfg.marker         = 'labels';
cfg.markerfontsize = 4;
cfg.zlim           = 'maxabs';
cfg.interpolatenan = 'no';
ft_topoplotER(cfg, append_opm_nan); 

print -dpng cuttingeegx_topo_no-interp_opm.png

Plot the topography including NaNs, then compare it with the topography where you excluded NaNs.

Coregistration

SQUID

We are now going to coregister the anatomical MRI to the SQUID coordinate system. We read the MRI, SQUID channels and the Polhemus headshape in memory. We recommend converting all quantities to SI units to ensure consistent units throughout your pipeline.

%% Loading files & converting to SI units

mri    = ft_read_mri('sub-01_acq-mprage_T1w.nii');
ctf275 = ft_read_sens('sub-01_ses-01_task-MedianNervesStim_squid.ds', 'senstype', 'meg');
shape  = ft_read_headshape('sub-01_ses-01_headshape.pos');

mri    = ft_convert_units(mri, 'm');
ctf275 = ft_convert_units(ctf275, 'm');
shape  = ft_convert_units(shape, 'm');

save mri mri
save ctf275 ctf275
save shape shape

To understand coregistration, you first need to know what coordinate systems are. Coregistration is about aligning data that is initially expressed in different coordinate systems into a single coordinate system.

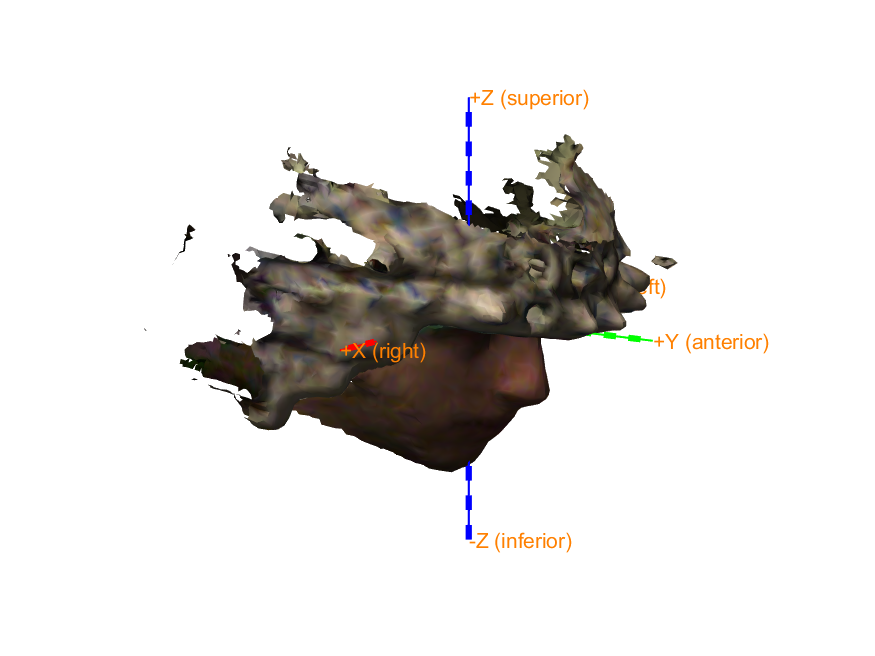
Start by plotting the MRI, SQUID sensors, and Polhemus headshape to see in which coordinate systems these are expressed. You can use ft_determine_coordsys for that.

We co-register the MRI to the SQUIDs by converting the MRI coordinate system to match that of the SQUIDs. In other words, we ensure that the three fiducials (Nasion, LPA and RPA) defined in the MRI coordinate system become aligned to the same three fiducials defined in the SQUID coordinate system.

%% Co-registering the anatomical MRI to the SQUID coordinate system

load shape shape
load ctf275 ctf275

% assign the 'ctf' coordinate system to the MRI 
cfg          = [];
cfg.method   = 'interactive';
cfg.coordsys = 'ctf'; % ALS coordinate system
mri_realigned1 = ft_volumerealign(cfg, mri);

save mri_realigned1 mri_realigned1

To refine the coregistration, we can also coregister the Polhemus head shape with the skin surface that is extracted from the previously aligned MRI. Now not only the fiducials but also other skin surface points acquired with the Polhemus are used for the alignment.

%% Refining co-registration using the Polhemus scan

load mri_realigned1 mri_realigned1

cfg = [];
cfg.method = 'headshape';
cfg.headshape.headshape = shape;
mri_realigned2 = ft_volumerealign(cfg, mri_realigned1); 

% check 
cfg = [];
cfg.method = 'headshape';
cfg.headshape.headshape = shape;
cfg.headshape.icp = 'no';
ft_volumerealign(cfg, mri_realigned2); 

save mri_realigned2 mri_realigned2

Let’s plot the sensor topography in 3D using ft_plot_topo3d. This will help us visualize where the sensors are positioned relative to the head. To make this clearer, we’ll also display the scalp and brain surfaces.

First, we’ll prepare the surface mesh of the scalp and brain:

%% Preparing the surface mesh of the scalp and brain

load mri_realigned2 mri_realigned2

cfg                = [];
cfg.output         = {'brain', 'scalp'};
mri_segmented      = ft_volumesegment(cfg, mri_realigned2);

cfg                = [];
cfg.tissue         = {'brain'};
mesh_brain         = ft_prepare_mesh(cfg, mri_segmented);

cfg                = [];
cfg.tissue         = {'scalp'};
mesh_scalp         = ft_prepare_mesh(cfg, mri_segmented);

save mesh_brain mesh_brain
save mesh_scalp mesh_scalp

Now, we’ll plot the 3D sensor topography for the time window [0.035, 0.050] seconds, along with the brain and scalp:

%% Plotting the 3D sensor topography

load mesh_brain mesh_brain
load mesh_scalp mesh_scalp
load avg_squid avg_squid
load ctf275 ctf275

% do not select the reference sensors
index  = startsWith(ctf275.label,'M');
pos275 = ctf275.chanpos(index,:);

% average the activity of interest in the time window [0.035 0.050] sec
sampling_rate = 1200; % in Hz
prestim = 0.2;

I1 = (prestim + 0.035) * sampling_rate; 
I2 = (prestim + 0.050) * sampling_rate;

selected_avg = mean(avg_squid.avg(:, I1:I2), 2);

% Plot
figure;
ft_plot_mesh(mesh_scalp, 'facealpha', 0.5, 'facecolor', 'skin', 'edgecolor', 'none', 'edgecolor', 'skin' )
hold on
ft_plot_mesh(mesh_brain, 'facecolor', 'brain', 'edgecolor', 'none');
hold on
ft_plot_topo3d(pos275, selected_avg, 'facealpha', 0.9)
camlight
view([90 0])

print -dpng cuttingeegx_topo3d_squid.png

OPM

We will coregister the OPMs with the MRI using an optical 3D scanner which captures the participant’s facial features along with the OPM helmet. First we read and plot the optical scan:

%% Loading files

scan      = ft_read_headshape('sub-01-ses-01_opticalscan.obj');
scan.unit = 'm'; % assign the correct unit

figure; hold on;
ft_plot_headshape(scan);
ft_plot_axes(scan);
lighting gouraud
material dull
light

We assign the RAS coordinate system to the scan.

%% Assign coordinate system

cfg          = [];
cfg.method   = 'fiducial';
cfg.coordsys = 'neuromag'; 
scan_aligned = ft_meshrealign(cfg, scan); 

figure; hold on;
ft_plot_headshape(scan_aligned);
ft_plot_axes(scan_aligned);
view([125 10]);
lighting gouraud
material dull
light

save scan_aligned scan_aligned

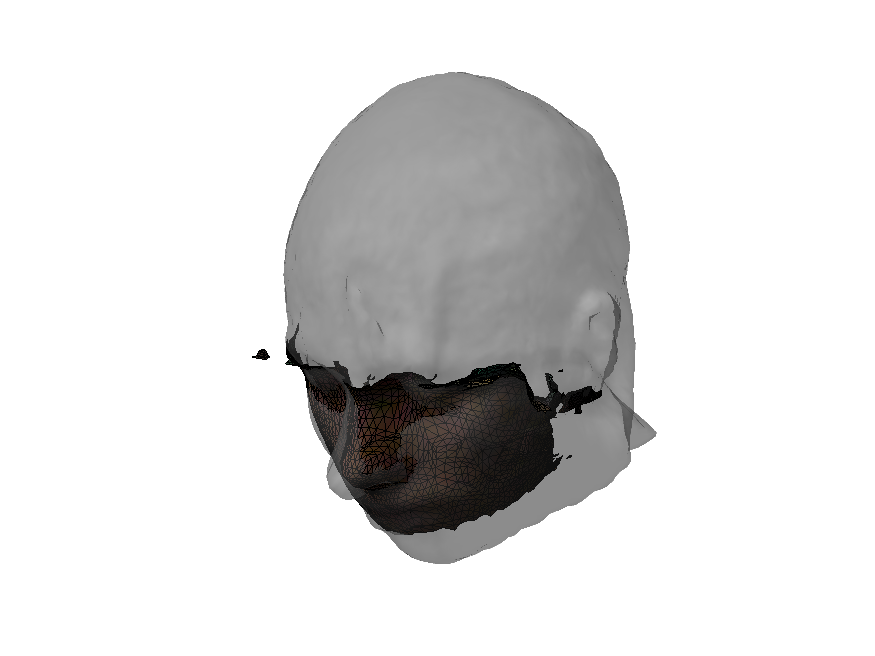
We remove irrelevant parts such as the body and cables. We use the ft_defacemesh function with a bounding box to keep only the desired head area.

%% Remove Body and Cables

cfg           = [];
cfg.method    = 'box';
cfg.selection = 'inside';
scan_head     = ft_defacemesh(cfg, scan_aligned); 

figure; hold on;
ft_plot_headshape(scan_head);
ft_plot_axes(scan_head);
view([125 10]);
lighting gouraud
material dull
light

save scan_head scan_head

We isolate the face region from the 3D scan using a bounding box. We will later align this face with the face extracted from the MRI.

%% Isolate face

cfg           = [];
cfg.method    = 'box';
cfg.selection = 'inside';
scan_face     = ft_defacemesh(cfg, scan_head);

figure; hold on;
ft_plot_headshape(scan_face);
ft_plot_axes(scan_face);
view([125 10]);
lighting gouraud
material dull
light

save scan_face scan_face

Next, we isolate the helmet region from the 3D scan using a bounding box. We will later align this helmet with the reference helmet (i.e., the 3D model of the actual FieldLine helmet).

%% Isolate helmet

cfg           = [];
cfg.method    = 'box';
cfg.selection = 'outside';
scan_helmet   = ft_defacemesh(cfg, scan_head);  

figure; hold on;
ft_plot_headshape(scan_helmet);
ft_plot_axes(scan_helmet);
view([125 10]);
lighting gouraud
material dull
light

save scan_helmet scan_helmet

We load the MRI. As the same participant took part in both SQUID and OPM recordings, we can reuse his/her segmented MRI from the SQUID analysis to save time:

load mri_segmented mri_segmented % from the SQUID analysis

We align face from the 3D scan with the face extracted from the MRI.

%% Aligning the face from the 3D scan with the face extracted from the MRI

% create a mesh for the scalp
cfg             = [];
cfg.tissue      = 'scalp';
cfg.numvertices = 10000;
mri_face        = ft_prepare_mesh(cfg, mri_segmented);

save scan_face_aligned scan_face_aligned

% alignment
cfg               = [];
cfg.method        = 'interactive';
cfg.headshape     = mri_face;
cfg.meshstyle     = {'edgecolor', 'k', 'facecolor', 'skin'};
scan_face_aligned = ft_meshrealign(cfg, scan_face);

figure; hold on;
ft_plot_headshape(mri_face, 'facealpha', 0.4);
ft_plot_mesh(scan_face_aligned, 'facecolor','skin');
view([125 10]);
lighting gouraud
material dull
light

We align the helmet from the 3D scan with the reference helmet. For this we use the 3D model of the actual FieldLine helmet. The reference helmet only contains the rim around the face.

%% Aligning the helmet from the 3D scan with the reference helmet

helmet_rim = ft_read_headshape('fieldlinebeta2_helmet_rim.mat');

cfg                 = [];
cfg.method          = 'interactive';
cfg.headshape       = helmet_rim;
cfg.meshstyle       = {'edgecolor', 'none', 'facecolor', [1 0.5 0.5]};
scan_helmet_aligned = ft_meshrealign(cfg, scan_helmet);

save scan_helmet_aligned scan_helmet_aligned

figure; hold on;
ft_plot_mesh(helmet_rim, 'edgecolor', 'none', 'facecolor', [0.5 0.5 1], 'facealpha', 0.4);
ft_plot_mesh(scan_helmet_aligned, 'edgecolor', 'none', 'facecolor', [1 0.5 0.5], 'facealpha', 0.4);
view([145 10]);
lighting gouraud
material dull
light

The three objects (the optical 3D scan, the face from the MRI and the template helmet) are initially all expressed in different coordinate systems. In the previous steps we have determined two pairwise transformations, which can be combined and used to align each of the objects to any other object.

Now we can use the transformation that aligns the face from the 3D scan with the face from the anatomical MRI and the transformation that aligns the helmet from the 3D scan with the reference helmet to calculate the transformation that aligns the reference helmet with the anatomical MRI.

%% Calculate transformation matrix

transform_scan2helmet = scan_helmet_aligned.cfg.transform;
transform_scan2face   = scan_face_aligned.cfg.transform;
transform_helmet2face = transform_scan2face/transform_scan2helmet;

The transformation matrix 'transform_helmet2face' can now be used to coregister the the OPM sensors with the MRI, which aligns the OPM sensors with head-based coordinate system. Before applying the transformation, we need to read the OPM sensors from the six fif files and combine them into a single sensor file. In the FieldLine system the OPM sensors slide into the smart helmet; the fif file contains the actual position of the sensors relative to the helmet.

%% Read and combine the sensors from the six recordings

f = dir('*.fif'); % add the whole path to your .fif files
f = struct2cell(f);

for i=1:6
    sensfile = fullfile(f{2,i},f{1,i});
    sens(i) = ft_read_sens(sensfile);
end

save sens sens

cfg      = [];
sens_combined = ft_appendsens(cfg, sens(1), sens(2), sens(3), sens(4), sens(5), sens(6)); % removes the duplicate channels

save sens_combined sens_combined

We apply the transformation to align the OPM sensors with head-based coordinate system.

%% Apply transformation matrix

fieldlinebeta2_head = ft_transform_geometry(transform_helmet2face, sens_combined);

save fieldlinebeta2_head fieldlinebeta2_head

figure; hold on;
ft_plot_sens(fieldlinebeta2_head, 'label', 'off');
ft_plot_headshape(mri_face, 'facecolor', [0.5 0.5 1], 'facealpha', 0.4, 'edgecolor', 'none');
view([125 10]);
lighting gouraud
material dull
light

Lastly, we plot the 3D sensor topography for the time window [0.035, 0.050] seconds, along with the scalp:

%% Plotting the 3D sensor topography

load mesh_brain mesh_brain % from the SQUID analysis
load mesh_scalp mesh_scalp % from the SQUID analysis
load fieldlinebeta2_head fieldlinebeta2_head
load append_opm append_opm

[i_avg, i_sens] = match_str(append_opm.label, fieldlinebeta2_head.label);

% average the activity of interest in the time window [0.035 0.050] sec
sampling_rate = 5000; % in Hz
prestim = 0.2;

I1 = (prestim+0.035)*sampling_rate; 
I2 = (prestim+0.050)*sampling_rate;

selected_avg = mean(append_opm.avg(:, I1:I2), 2);

% Plot
figure;
ft_plot_mesh(mesh_scalp, 'facealpha', 0.05, 'facecolor', 'skin', 'edgecolor', 'none', 'edgecolor', 'skin' )
hold on
ft_plot_topo3d(fieldlinebeta2_head.chanpos(i_sens,:), selected_avg(i_avg), 'facealpha', 1)
camlight
view([90 0])

print -dpng cuttingeegx_topo3d_no-interp_opm.png

Why do you think there’s a gap on the right side of the topography? Hint: Interpolation.

How do the 3D sensor topographies of OPMs and SQUIDs differ, and what causes these differences?

 

Tags: cuttingeegx