Classification of event-related MEG data using MVPA-Light

Introduction

The objective of this tutorial is to give an introduction to the classification of event-related data using the MVPA-Light toolbox. For a general introduction to the toolbox refer to the MVPA-Light paper. The MVPA-Light readme file is the most up to date reference. This tutorial builds on skills acquired in the preprocessing, event-related averaging and time-frequency analysis tutorials.

Installation

MVPA-Light is a stand-alone MATLAB toolbox for multivariate pattern analysis involving classification or regression. It features cross-validation, various classifiers, regression models, performance metrics, as well as nested preprocessing and hyperparameter selection. FieldTrip provides a high-level interface to its functions so one does not need to directly interact with the toolbox. However, it needs to be installed and included in MATLAB’s search path. To this end, follow the installation instructions on its GitHub page.

Procedure

We will use classifiers to analyze the MEG-language dataset which features one subject with three types of trials: fully incongruent (FIC), fully congruent (FC), and initially congruent (IC). These three classes are stored in different files available here: dataFIC_LP.mat, dataFC_LP.mat and dataIC_LP.mat.

The data can be loaded into MATLAB using

load dataFIC_LP
load dataFC_LP
load dataIC_LP

To get started, we investigate whether we can discriminate between the three classes FIC, FC, and IC, using the average activity in the 0.5-0.7 s post-stimulus interval.

After this, we will focus on two out of the three classes, namely FIC vs FC, and we will investigate the following questions:

• At what times (‘when’) in a trial can one discriminate between FIC and FC?
• At which sensor locations (‘where’) can one discriminate between FIC and FC?
• Which representations that discriminate between FIC and FC generalize across time?

Note that the classification is performed for a single subject using single trials.

Classification in the 0.5-0.7 s interval

We will use ft_timelockstatistics to determine the classification accuracy between the three classes FIC, FC, and IC. As features, the average activity in each MEG channel in the the 0.5-0.7 s interval is used. In each trial, this yields 149 features for the classifier, one feature per MEG channel. Let us first determine the number of trials in each class:

nFIC = numel(dataFIC_LP.trial);
nFC = numel(dataFC_LP.trial);
nIC = numel(dataIC_LP.trial);

Define the configuration struct

cfg = [] ;
cfg.method          = 'mvpa';
cfg.latency         = [0.5, 0.7];
cfg.avgovertime     = 'yes';
cfg.design          = [ones(nFIC,1); 2*ones(nFC,1); 3*ones(nIC,1)];
cfg.features        = 'chan';
cfg.mvpa            = [];
cfg.mvpa.classifier = 'multiclass_lda';
cfg.mvpa.metric     = 'accuracy';
cfg.mvpa.k          = 3;

Let us unpack this:

• cfg.method = 'mvpa' indicates that we want to perform multivariate pattern analysis using MVPA-Light. Classification is performed for every time point (see section Classification across time).
• cfg.latency restricts the classification analysis to a specific time window (here 0.5-0.7s).
• cfg.avgovertime specifies whether the activity in latency window should be averaged prior to classification.
• cfg.design specifies the vector of class labels. Class labels indicate which class (or experimental condition) trials belong to. The task of the classifier is to predict these class labels given the data. To this end, we create a vector with 1’s for the trials belonging to class 1, 2’s for trials belonging to class 2, and so on. The MEG-language dataset, comprises three classes, namely FIC (class 1), FC (class 2), and IC (class 3). You can also use a different set of numbers (e.g., trigger codes) to denote the classes. MVPA-Light then internally translates them into 1’s, 2’s and 3’s.
• cfg.features indicates which of the data dimensions we want to use as features (channels in this case). The name should correspond to the name of the dimension in the cfg.dimord field. All data dimensions that are not samples or features are considered as search dimensions. A separate multivariate analysis is conducted for every coordinate in the search dimensions. For instance, imagine the dimensions of the data are [samples x chan x time]. If cfg.features = 'chan' then time serves as a search dimension and a separate analysis is performed for every time point. If cfg.features = 'time' then chan serves as the search dimension and a separate analysis is performed for every channel.
• cfg.mvpa is a struct that controls properties of the multivariate analysis including cross-validation settings, selection of the classifier and performance metrics. It is directly passed on to MVPA-Light.
• cfg.mvpa.classifier indicates which classifier we want to use. Here, we use multi-class Linear Discriminant Analysis (LDA). Click here for a full list of available classifiers.
• cfg.mvpa.metric indicates the metric we use to measure classifier performance. Here, classification accuracy is used. Other metrics such as AUC and F1-score are available. Click here for a full list of available metrics.
• cfg.mvpa.k specifies the number of folds used to calculate the cross-validated performance. Cross-validation is explained in more detail in the next section.

Now call

stat = ft_timelockstatistics(cfg, dataFIC_LP, dataFC_LP, dataIC_LP)

to perform the classification analysis. It is important to make sure that the order of class labels (FIC, FC, IC) matches the order that the datasets are passed in to ft_timelockstatistics. It is not required that each class is contained in a separate dataset. The same result can be achieved when all classes are part of one dataset dat. To illustrate this, append the data and then pass it to ft_timelockstatistics:

dat = ft_appenddata([], dataFIC_LP, dataFC_LP, dataIC_LP);
stat = ft_timelockstatistics(cfg, dat);

The resulting classification accuracy can slighty vary due to the random assignment of samples into folds. Let us print the resulting classification accuracy

fprintf('Classification accuracy: %0.2f\n', stat.accuracy)

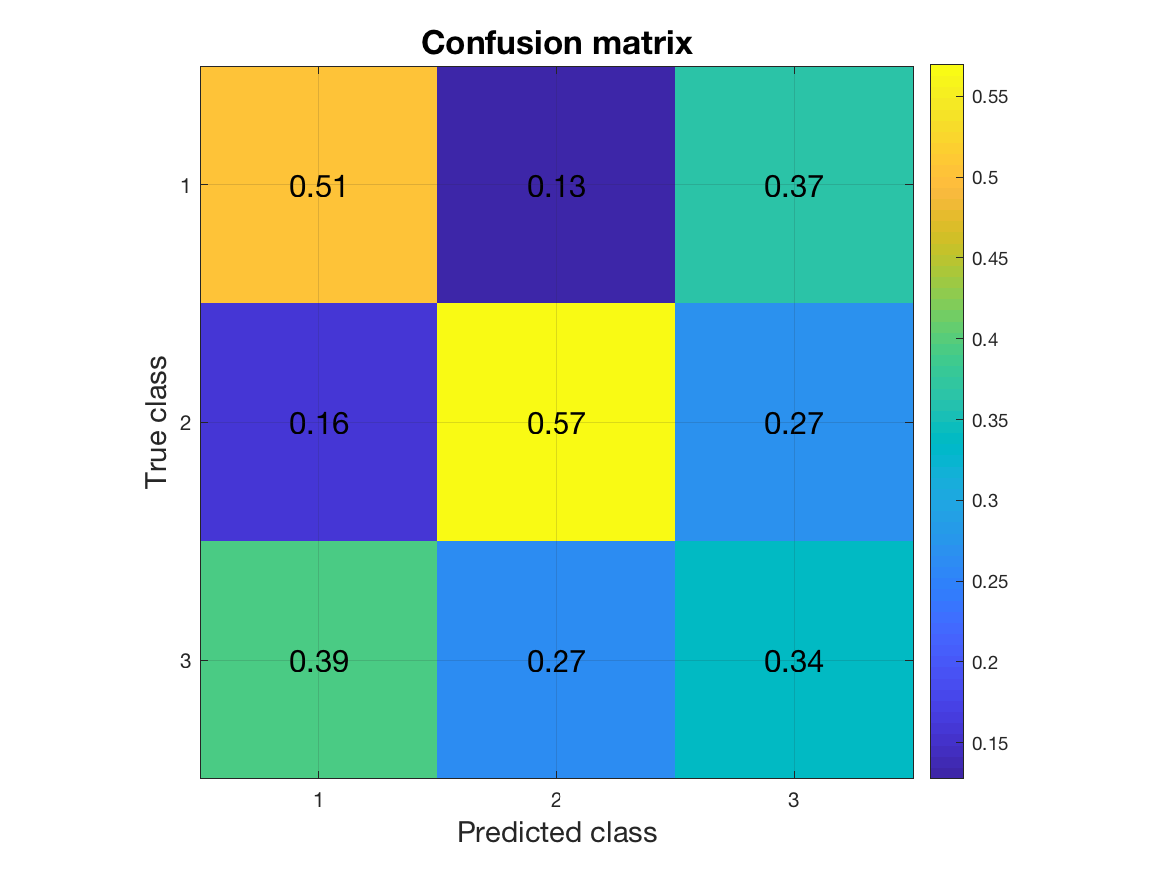
For multi-class problems, the confusion matrix is a useful metric. In a confusion matrix, rows correspond to the true class labels, columns correspond to predicted class labels. The (i,j)-th element gives the proportion of samples of class i that have been classified as class j. Consequently, the diagonal of the confusion matrix contains the proportion of correct classifications. Off-diagonal elements specify the misclassifications. To obtain the confusion matrix, all we need to do is to change the metric field:

cfg.mvpa.metric      = 'confusion';
stat = ft_timelockstatistics(cfg, dataFIC_LP, dataFC_LP, dataIC_LP)

stat.confusion

Looking at the diagonal of the matrix tells us that the classifier is better at predicting classes 1 and 2 than it is at predicting class 3. For a simple visualization of this result, we can use a plotting function in MVPA-Light called mv_plot_result. It takes the result structure returned in stat.mvpa which contains the classification results in a format required by the function.

mv_plot_result(stat.mvpa)

Cross-validation

To obtain a realistic estimate of classifier performance and control for overfitting, a classifier should be tested on an independent dataset that has not been used for training. In most neuroimaging experiments, there is only one dataset with a restricted number of trials. K-fold cross-validation makes efficient use of this data by splitting it into k different folds. In each iteration, one of the k folds is held out and used as test set, whereas all other folds are used for training the model. This process is repeated until every fold has been used as test set once. Other cross-validation schemes supported by MVPA-Light are leave-one-out cross-validation, holdout, and predefined folds. Cross-validation is controlled by the following parameters:

• cfg.mvpa.cv: cross-validation type, either ‘kfold’, ‘leaveout’, ‘holdout’, or ‘predefined’ (default ‘kfold’)
• cfg.mvpa.k: number of folds or partitions in k-fold cross-validation (default 5)
• cfg.mvpa.repeat: number of times the whole cross-validation analysis is repeated with new randomly assigned folds (default 5)
• cfg.mvpa.p: if cfg.mvpa.cv is ‘holdout’, p is the fraction of test samples (default 0.1)
• cfg.mvpa.stratify: if 1, the class proportions are approximately preserved in each test fold (default 1)
• cfg.mvpa.fold: if cv=’predefined’, fold is a vector of length #samples that specifies the fold each sample belongs to

For k-fold cross-validation, the total number of training and testing iterations is equal to cfg.k * cfg.repeat. The result returned by ft_timelockstatistics is always the average across all test folds and repetitions.

Exercise 1

Search across time (‘when’)

Many neuroimaging datasets have a 3-D structure [trials x channels x time]. Classification across time can help identify the time points in a trial when discriminative information shows up. To this end, classification is performed for each time point separately. First, we need to make sure that the time dimension is not averaged out. We can set cfg.avgovertime = 'no', but since the default value is 'no' we can simply omit this parameter.

cfg = [] ;
cfg.method           = 'mvpa';
cfg.features         = 'chan';
cfg.mvpa.classifier  = 'lda';
cfg.mvpa.metric      = 'auc';
cfg.mvpa.k           = 10;
cfg.mvpa.repeat      = 2;
cfg.design           = [ones(nFIC,1); 2*ones(nFC,1)];

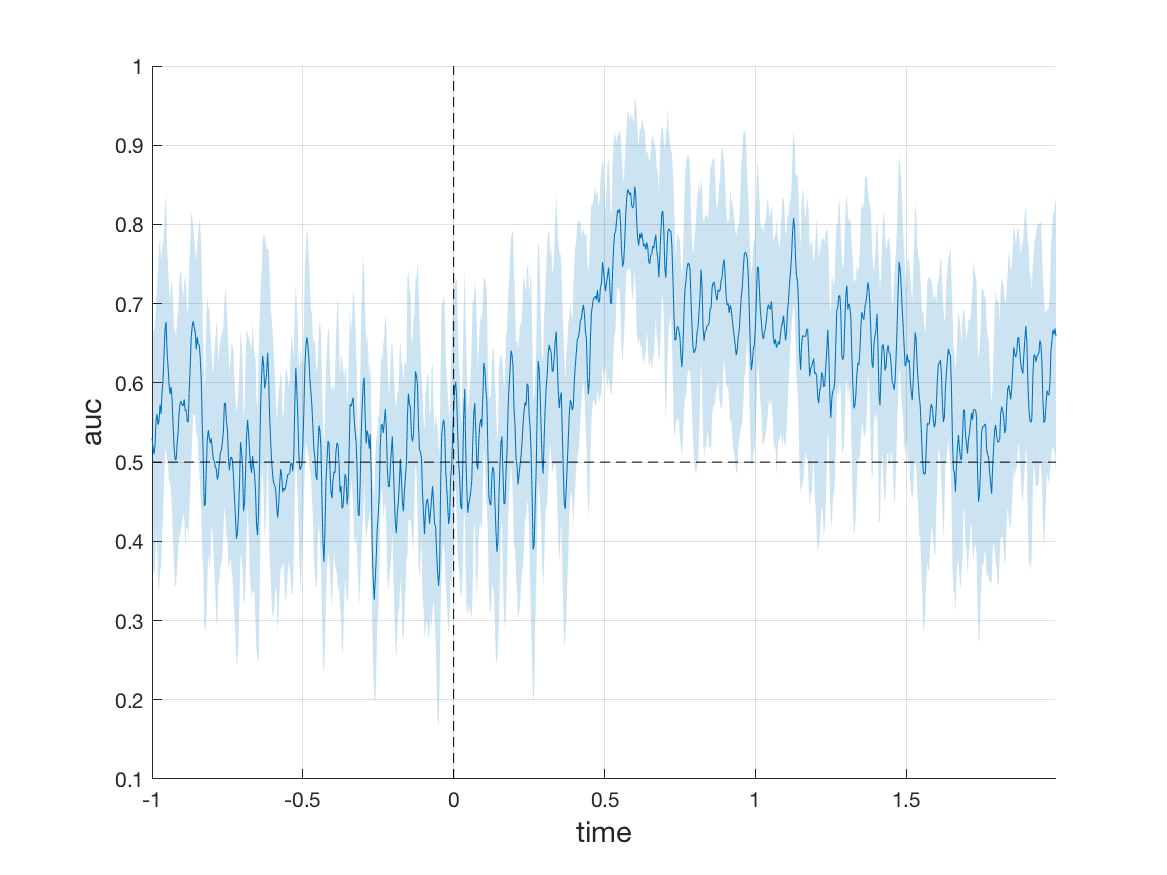
For simplicity, we will limit ourselves to comparing only FIC and FC. As classifier, we use Linear Discriminant Analysis (LDA). As metric, we use area under the ROC curve (AUC). It is calculated using 10-fold cross-validation with 2 repetitions.

stat = ft_timelockstatistics(cfg, dataFIC_LP, dataFC_LP);

Note that the metric is now a vector with 900 values, one AUC value for each time point in the trial. It can be plotted as a function of time using

plot(stat.auc)

For a slightly nicer plot, one can again use mv_plot_result. As a second parameter, we pass the time values to make sure that the x-axis is formatted correctly.

mv_plot_result(stat.mvpa, stat.time)

The resultant plot shows AUC across time in the trial. The shaded area is the standard deviation of the AUC metric across the different test sets in the cross-validation.

Exercise 2

Search across channels (‘where’)

Which channels contribute most to classification performance? The answer to this question can be used to better interpret the data or to perform feature selection. To this end, we will perform a separate classification analysis for each channel.

cfg = [] ;
cfg.method        = 'mvpa';
cfg.latency       = [0.3, 0.7];
cfg.avgovertime   = 'yes';
cfg.features      = 'time';
cfg.design        = [ones(nFIC,1); 2*ones(nFC,1)];
stat = ft_timelockstatistics(cfg, dataFIC_LP, dataFC_LP)

Since we did not specify a classifier and a metric, the default values (LDA as classifier and classification accuracy as metric) are used. In searchlight analysis, the time points in a trial are used as features, for each channel separately. Set cfg.latency to restrict the analysis to a specific time window. Set cfg.features = 'time' to indicate that the time dimension serves as features. If we would set cfg.features = 'chan', all channels would be used as features at once. Note that since the time dimension is a singleton dimension (we are averaging over time) you could also set cfg.features = [] instead of cfg.features = 'time'.

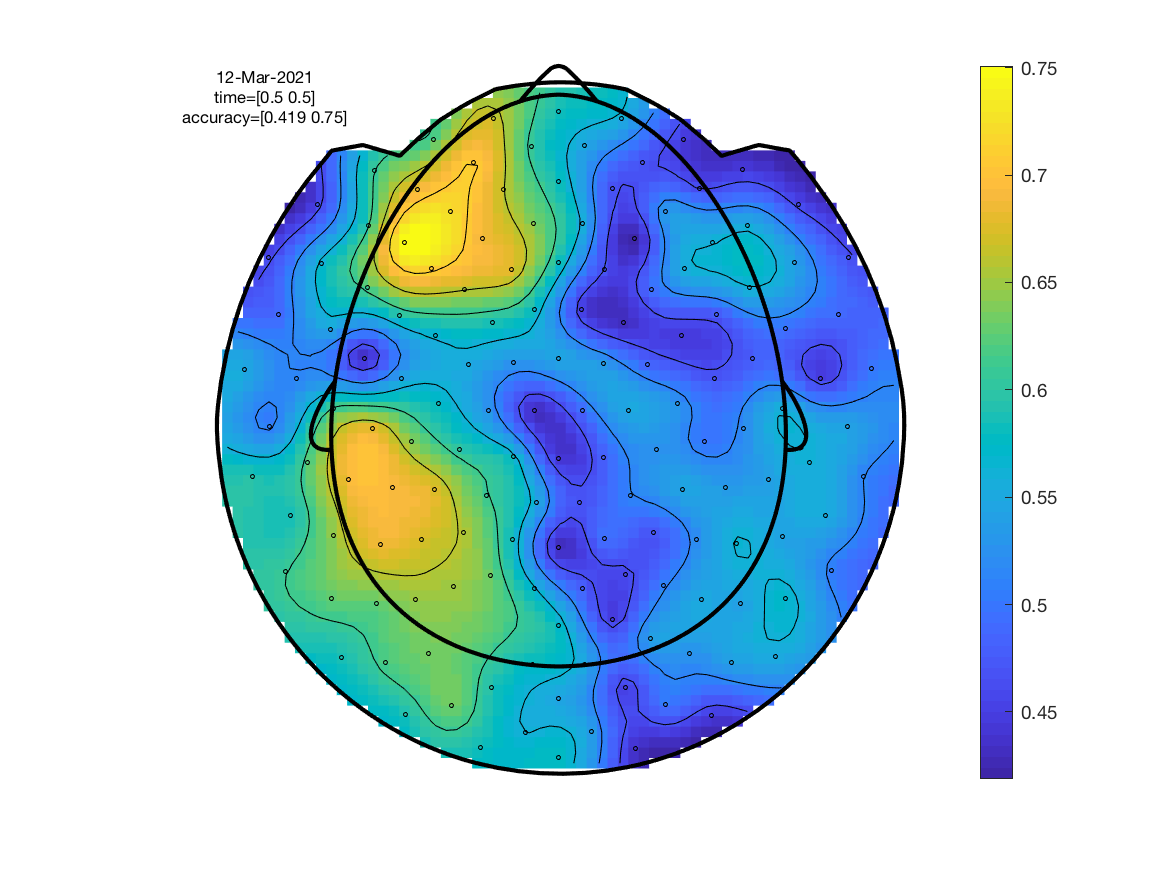
Since a classification result is obtained for each channel, classification accuracy can be plotted as a topography. We call ft_topoplotER to do the plotting.

cfg              = [];
cfg.parameter    = 'accuracy';
cfg.layout       = 'CTF151_helmet.mat';
cfg.xlim         = [0, 0];
cfg.colorbar     = 'yes';
ft_topoplotER(cfg, stat);

Exercise 3

In the previous analysis, classification has been performed for each channel separately. However, the spatial arrangement of MEG channels can be exploited in order to group neighbouring channels as features in the searchlight. To build the neighbourhood structure, we use ft_prepare_neighbours.

cfg = [];
cfg.method      = 'triangulation';
cfg.layout      = 'CTF151_helmet.mat';
cfg.channel     = dataFC_LP.label;
neighbours = ft_prepare_neighbours(cfg);

We are now ready to re-run the searchlight analysis. We can pass the neighbourhood structure via the parameter cfg.neighbours.

  cfg = [] ;
  cfg.method        = 'mvpa';
  cfg.features      = 'time';
  cfg.design        = [ones(nFIC,1); 2*ones(nFC,1)];
  cfg.latency       = [0.3, 0.7];
  cfg.avgovertime   = 'yes';

  cfg.neighbours  = neighbours;

  stat = ft_timelockstatistics(cfg, dataFIC_LP, dataFC_LP)

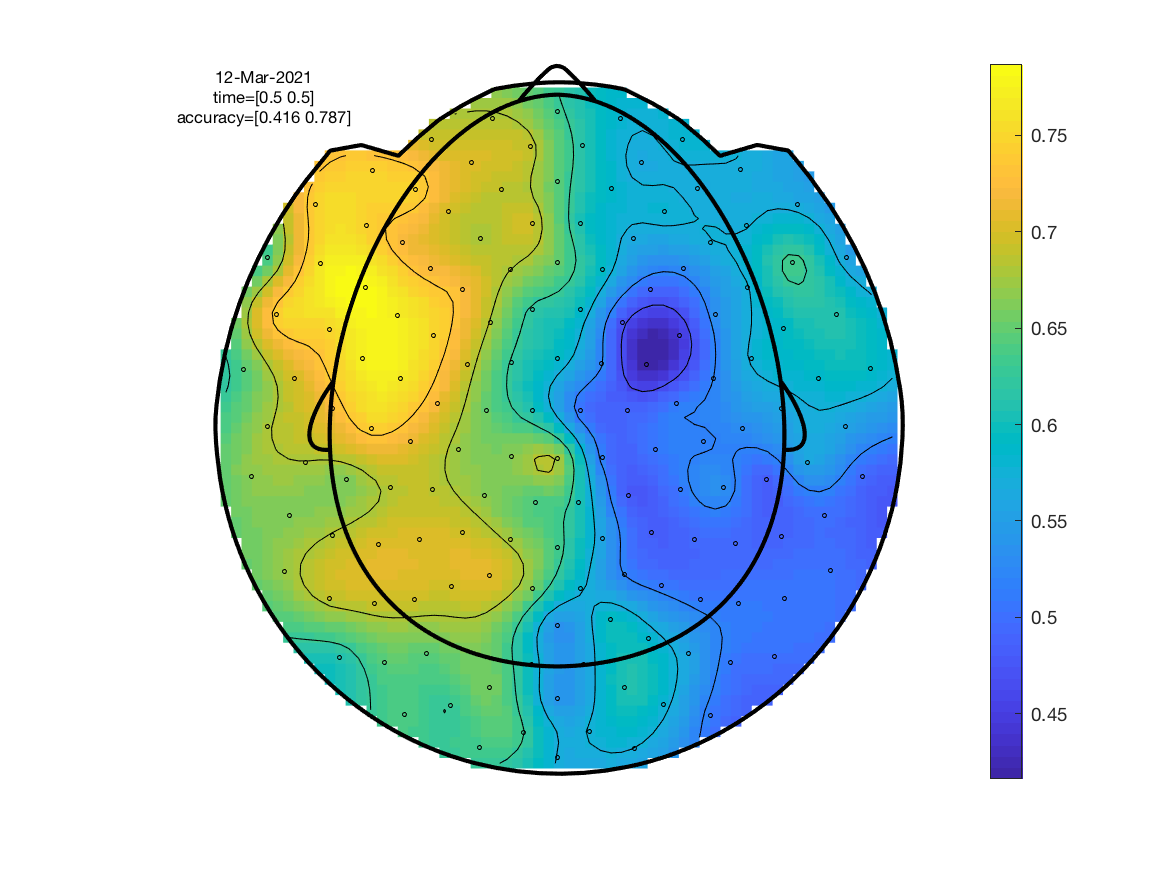
Call ft_topoplotER to plot the result as a topography.

  cfg              = [];
  cfg.parameter    = 'accuracy';
  cfg.layout       = 'CTF151_helmet.mat';
  cfg.xlim         = [0, 0];
  cfg.colorbar     = 'yes';
  ft_topoplotER(cfg, stat);

As expected, the resultant topography is slightly more smeared out. Peak classification accuracy is higher which is due to the classifier now combining information across neighbouring channels.

Search across both time and channels

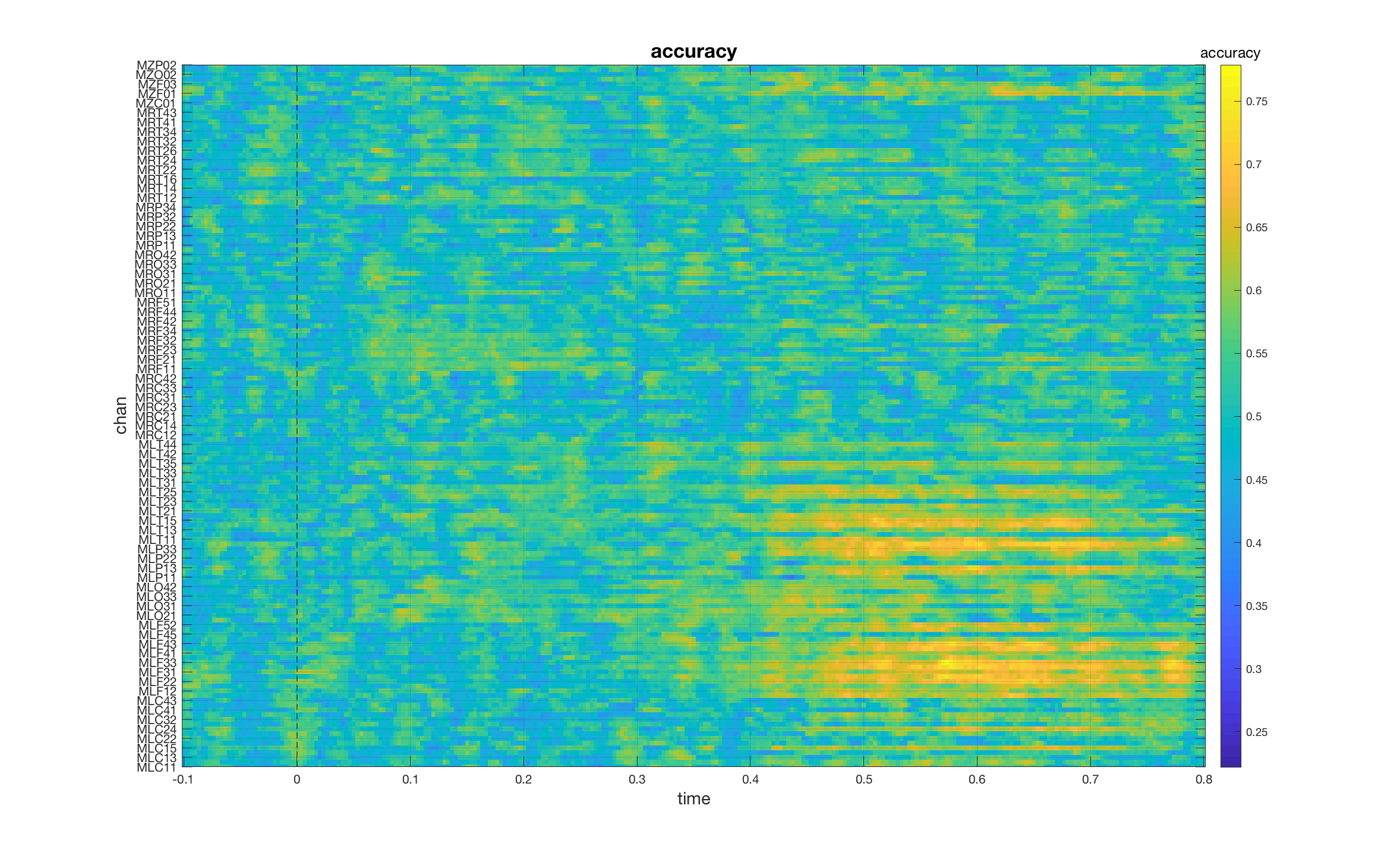
Notice the symmetry between the previous two analyses: for the ‘when’ analysis, we performed a classification for each time point using channels as features, for the ‘where’ analysis we performed a classification for each channel using time points as features. We select between these two analyses by setting cfg.features to either 'chan' or 'time'. What happens if we set cfg.features = []?

cfg = [] ;
cfg.method        = 'mvpa';
cfg.latency       = [-0.1, 0.8];
cfg.features      = [];
cfg.mvpa.repeat   = 2;
cfg.design        = [ones(nFIC,1); 2*ones(nFC,1)];
stat = ft_timelockstatistics(cfg, dataFIC_LP, dataFC_LP)

In this case, both channels and time points act as search dimensions and the result is a [chan x time] matrix of classification accuracies. If we plot the result, we can see which of the channels carry discriminative information and when.

mv_plot_result(stat.mvpa, stat.time)
set(gca, 'YTick', 1:2:length(stat.label), 'YTickLabel', stat.label(1:2:end))

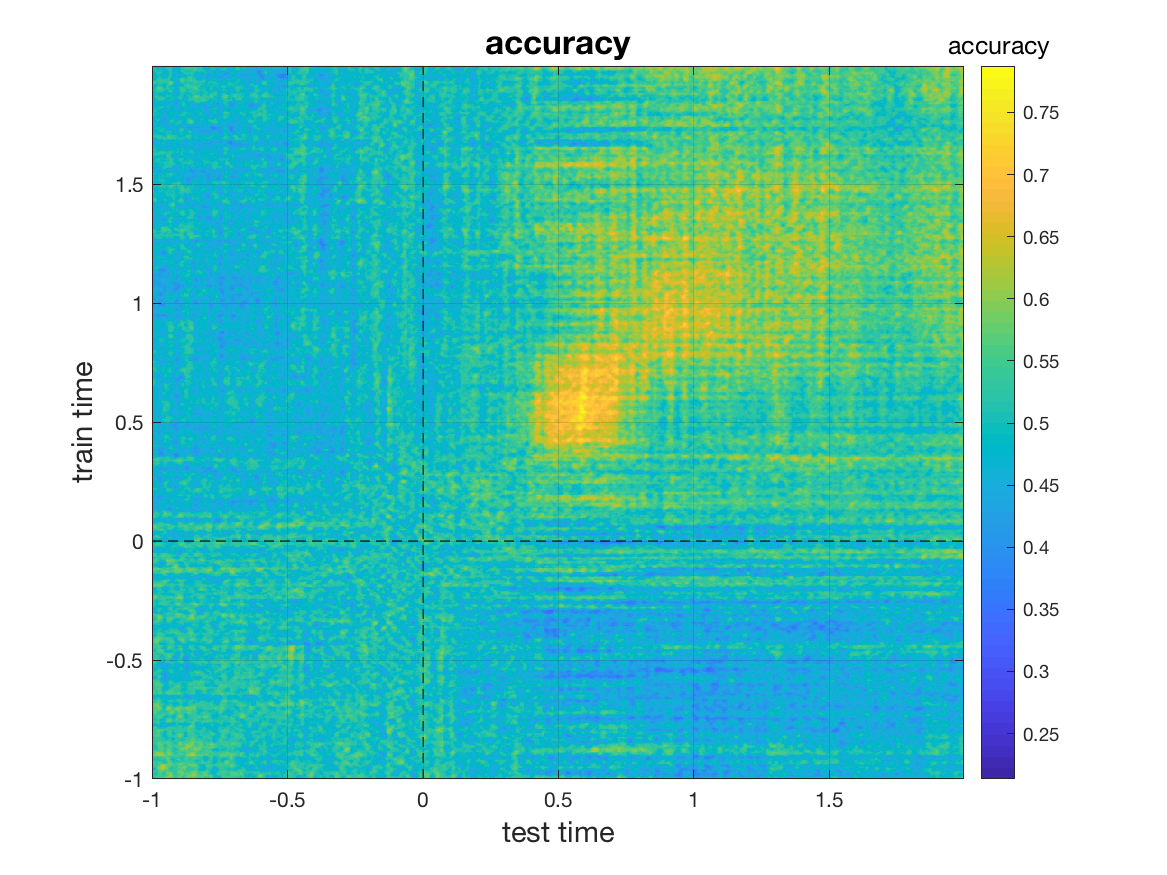
Time generalization (time x time classification)

Classification across time does not give insight into whether information is shared across different time points. For example, is the information that the classifier uses early in a trial (t=80 ms) the same that it uses later (t=300ms)? In time generalization, this question is answered by training the classifier at a certain time point t. The classifier is then tested at the same time point t but it is also tested at all other time points in the trial (King and Dehaene, 2014). This procedure is then repeated for every possible training time point. To perform time x time classification, we need to set the cfg.generalize parameter:

cfg = [] ;
cfg.method           = 'mvpa';
cfg.features         = 'chan';
cfg.generalize       = 'time';
cfg.design           = [ones(nFIC,1); 2*ones(nFC,1)];

stat = ft_timelockstatistics(cfg, dataFIC_LP, dataFC_LP);

It returns a 2-D matrix of classification performances, with performance calculated for each combination of training time point and testing time point. We plot the result using mv_plot_result. As parameters, we pass the classification result. To lay out the axes, we pass stat.time twice, once for the x-axis and once for the y-axis.

mv_plot_result(stat.mvpa, stat.time, stat.time)

In the resultant plot, each row (corresponding to a value of on the y-axis) corresponds to the time point at which the classifier was trained. Each point on the x-axis corresponds to a time point at which the respective classifier was tested. The classifier attains peak performance roughly in the 0.45-0.65s period.

Classification of time-frequency data

The techniques we explored for 3-D [samples x chan x time] data seamlessly generalize to higher-dimensional datasets. For instance, let us consider 4-D [samples x chan x freq x time] data. We create such a dataset by performing a time-frequency analysis on the timelocked data (see Time-frequency analysis using Hanning window, multitapers and wavelets for details on time-frequency analysis).

  cfg              = [];
  cfg.output       = 'pow';
  cfg.method       = 'mtmconvol';
  cfg.taper        = 'hanning';
  cfg.keeptrials   = 'yes';
  cfg.foi          = 2:1:30;
  cfg.t_ftimwin    = ones(length(cfg.foi),1) * 0.5;
  cfg.toi          = -0.5:0.05:1.5;

  freqFIC = ft_freqanalysis(cfg, dataFIC_LP);
  freqFC = ft_freqanalysis(cfg, dataFC_LP);

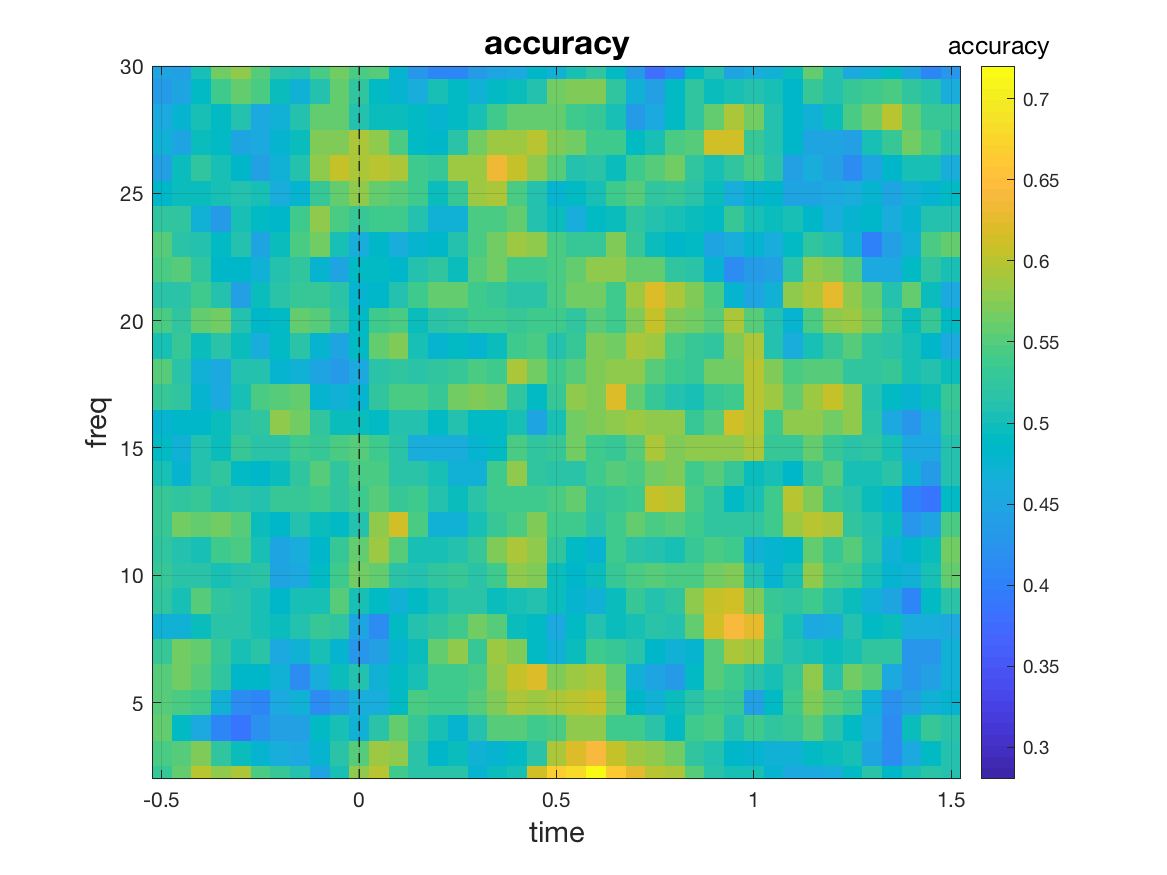
We aim to perform classification for each time-frequency point separately using channels as features. To this end, we only need to set cfg.features = 'chan'.

cfg = [] ;
cfg.method        = 'mvpa';
cfg.features      = 'chan';
cfg.design        = [ones(nFIC,1); 2*ones(nFC,1)];

stat = ft_freqstatistics(cfg, freqFIC, freqFC);

mv_plot_result(stat.mvpa, stat.time, stat.freq)

This yields a [freq x time] matrix of classification accuracies. However, we are not limited to a classification for every time-frequency point. A large array of different multivariate analyses can be realized by changing the value of cfg.features. Let us look at some of the options:

• cfg.features = 'time': if time serves as features, a search is performed across channels and frequencies. Therefore, the result is a [chan x freq] matrix of classification accuracies.
• cfg.features = 'freq': the result is a [chan x time] matrix of classification accuracies.
• cfg.features = []: in this case, a search is performed across all dimensions yielding a [chan x freq x time] array.
• cfg.features = {'chan' 'freq'}: multiple feature dimensions can be specified by providing a cell array. In this example, channels and frequencies are combined into a long feature vector and a classification is performed for every time point, yielding a [time x 1] vector.

Exercise 4

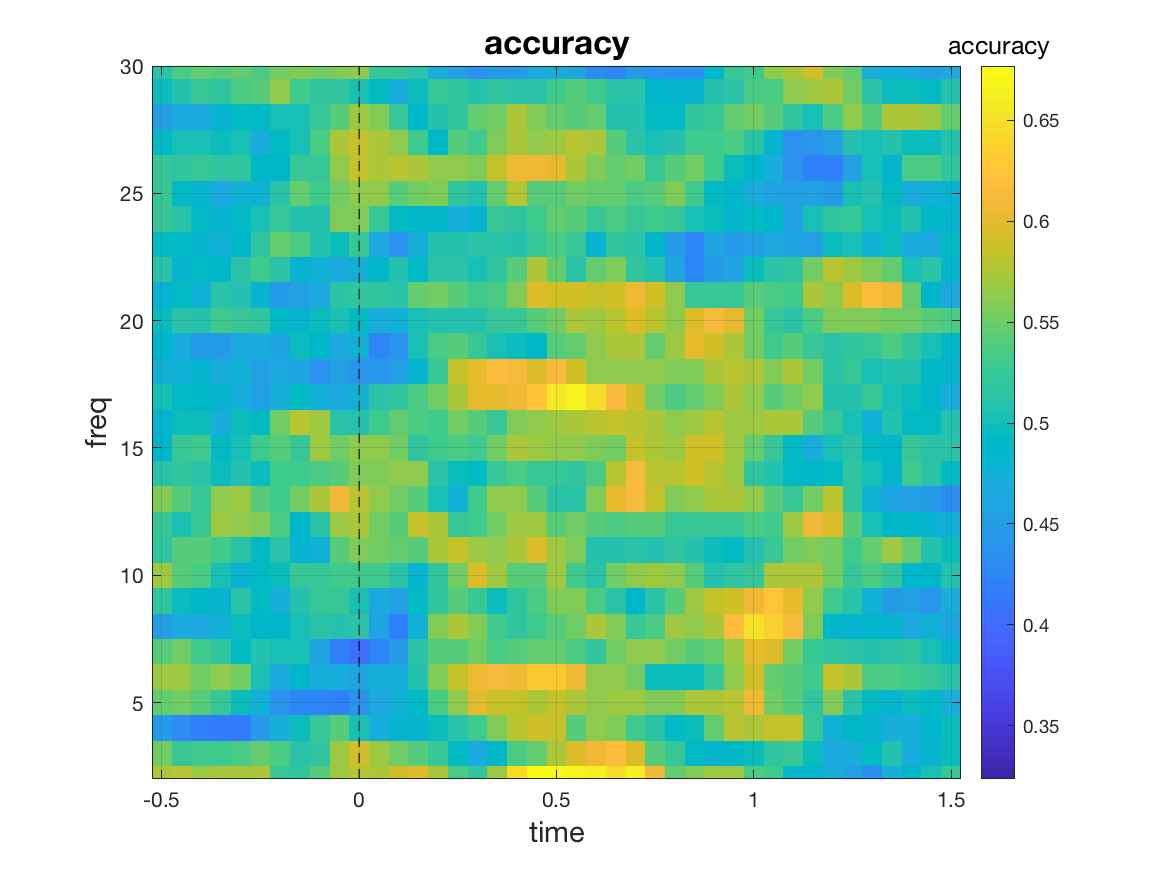
Similar to what we did in the ‘where’ analysis, we can control the size of the searchlight by specifying neighbouring channels/times/frequencies for each of the search dimensions. As an example, let us run an analysis across frequencies and time, this time taking into account neighbouring time points as well. To this end, we set cfg.timwin = 5 which means that a total of 5 time points is considered in each analysis: the given center time point and its two immediately preceding and following time points. Including neighbouring channels/frequencies/time points increases the dimensionality of the feature space. In this example, the feature space has the dimension 149 (channel) x 5 (time points) = 745. A larger feature space provides more information to the classifier but it also is more computationally demanding and potentially holds the danger of overfitting.

cfg = [] ;
cfg.method        = 'mvpa';
cfg.features      = 'chan';
cfg.design        = [ones(nFIC,1); 2*ones(nFC,1)];
cfg.timwin        = 5;

stat = ft_freqstatistics(cfg, freqFIC, freqFC);

mv_plot_result(stat.mvpa, stat.time, stat.freq)

Note that setting cfg.timwin is only useful if time is not used as features, and the same logic applies to cfg.freqwin (for frequencies) and cfg.neighbours (for channels).

Exercise 5

Hyperparameters

Many classifiers have parameters that control their properties and need to be set by the user, so-called hyperparameters. For a list of hyperparameters for each classifier, see the respective train_ functions in the model folder. The default values suffice for many scenarios, but sometimes you may want to manually change the parameters. This can be easily done using the hyperparameter substruct. For instance, in Support Vector Machines (SVM), the type of kernel is a hyperparameter. If an RBF kernel is used the parameter gamma controls the kernel width:

cfg.mvpa.hyperparameter           = [];
cfg.mvpa.hyperparameter.kernel    = 'rbf';
cfg.mvpa.hyperparameter.gamma     = 1;

See train_svm for a full list of SVM hyperparameters and their default values.

To give another example, in LDA the lambda parameter controls the amount of regularization of the covariance matrix. The default value 'auto' is usually sufficient but we can also set it to a specific value:

cfg.mvpa.hyperparameter           = [];
cfg.mvpa.hyperparameter.lambda    = 0.01;

See train_lda for a full list of LDA hyperparameters and their default values.

Exercise 6

Preprocessing

In this example we look into preprocessing pipelines. Preprocessing includes demeaning, z-scoring, PCA, sample averaging, feature extraction methods such as PCA, and any other approaches that operate on the data prior to training.

It is important to distinguish between global vs nested preprocessing. In global preprocessing, an operation is applied to the whole dataset (including both train and test data) at once before classification is done. This holds the possibility of information transfer between train and test set, since the operation applied to the train data is affected by the properties of the test data.

Nested preprocessing avoids this by obtaining the parameters for an operation solely from the train data. The parameters (e.g., principal components) extracted from the train set are then applied to the test set. This assures that no information from the test set goes into the preprocessing of the train data. Nested preprocessing can be triggered by using the cfg.mvpa.preprocess field. Let us first copy-paste the code used for the classification of the ERP peak from the beginning of this tutorial

cfg = [] ;
cfg.method          = 'mvpa';
cfg.features        = 'chan';
cfg.latency         = [0.5, 0.7];
cfg.avgovertime     = 'yes';
cfg.design          = [ones(nFIC,1); 2*ones(nFC,1); 3*ones(nIC,1)];
cfg.mvpa            = [];
cfg.mvpa.classifier = 'multiclass_lda';
cfg.mvpa.metric     = 'accuracy';
cfg.mvpa.k          = 3;

To perform nested z-scoring, we add the following line

cfg.mvpa.preprocess = 'zscore';

Nested z-scoring means that the means and standard deviations are calculated on the train data and then applied to both train and test data. This assures that no information from the test set flows into the processing of the train set. The available preprocessing functions are listed in the preprocess folder on the GitHub page. You can specify an operation by omitting mv_preprocess_. For instance, the file mv_preprocess_demean corresponds to the string 'demean'. We can follow up the z-score with a Principal Components Analysis (PCA) by providing both strings as a cell array

cfg.mvpa.preprocess = {'zscore' 'pca'};

Preprocessing functions also have parameters that control their behaviour. For instance, in PCA the number of PCs is such a parameter. Its default value is 20. Studying the help of the PCA function

help mv_preprocess_pca

we see that the parameter n controls the number of PCs. To change it, you can use the cfg.preprocess_param field. Since our preprocessing pipeline contains two operations cfg.preprocess_param is a cell array with two elements. PCA is the second preprocessing operation, so we need to set the second cell. We can provide parameters as key-value pairs. For instance, to set the number of PCs n = 10 we write:

cfg.mvpa.preprocess_param = {};
cfg.mvpa.preprocess_param{2} = {'n' 10};

Finally, let’s carry out the analysis.

stat = ft_timelockstatistics(cfg, dataFIC_LP, dataFC_LP, dataIC_LP)

The understanding preprocessing tutorial on the GitHub page covers preprocessing in more detail. Although the tutorial uses MVPA-Light directly, not through its FieldTrip interface, you can translate the code into FieldTrip by replacing all instances of cfg.preprocess by cfg.mvpa.preprocess.

Summary

In this tutorial, we explored the usage of MVPA-Light for the classification of time-locked and time-frequency data. By setting the parameters cfg.features and cfg.generalize cross-validated multivariate analyses can be flexibly designed. We further investigated the setting of hyperparameters and the construction of a nested preprocessing pipeline.