Computing and reporting the effect size
It is good practice to compute and report the size of the effect that you are studying: see for example the 2019 OHBM Committee on Best Practice in Data Analysis and Sharing (COBIDAS) recommendation Best Practices in Data Analysis and Sharing in Neuroimaging using MEEG or the 2013 Good practice for conducting and reporting MEG research guidelines.
The effect size is a way of quantifying the magnitude of an effect on your data. It can be quantified in different ways, e.g., as the uV difference in ERP amplitude on a specific channel at a specific latency following stimulus presentation, or as a standardized measure such as Cohen’s d.
This specific example starts with a ROI that is based on visual inspection, i.e. picking the channel and time window with the highest effect. Note, however, that this is only for didactical reasons. In reality it would be inappropriate to test only the largest observed effect. Rather, in the absence of an a priori region and/or latency of interest, you should test all channels and time points and correct for multiple comparisons to ensure that you are controlling the false alarm rate.
If you are doing hypothesis-driven research, you should not guide your statistical analysis by a visual inspection of the data; you should state your hypothesis up-front and avoid data dredging or p-hacking.
On the other hand: if you are doing exploratory research, you should not compute p-values. Effect sizes are interesting and relevant to report for both exploratory and hypothesis-driven research.
The ERF_orig.mat data that is used in this example script is available from our download server. The same data is used in the other statistics tutorials; the example here specifically follows the Parametric and non-parametric statistics on event-related fields tutorial.
The already preprocessed data is based on 151-channel MEG recordings from 10 subjects and consists of single-subject event-related averages for an auditory language task with two conditions: fully incongruent (FIC) and fully congruent (FC) sentence endings. See the other tutorials on the meg-language dataset for more details.
load ERF_orig; % averages for each individual subject, for each condition
Using ft_timelockgrandaverage with the cfg.keepindividual option allows us to represent the data in a more convenient format for the subsequent computations:
cfg = [];
cfg.keepindividual = 'yes';
grandavgFIC = ft_timelockgrandaverage(cfg, allsubjFIC{:});
grandavgFC = ft_timelockgrandaverage(cfg, allsubjFC{:});
In the other tutorial we have identified channel ‘MLT12’ to show the expected N400 effect in the time range from 300 to 700 ms following the onset of the critical word. We can specifically look at the effect at that channel by averaging over time, i.e. we define a “region of interest” in the data.
cfg = [];
cfg.channel = 'MLT12';
cfg.latency = [0.3 0.7];
cfg.avgoverchan = 'no'; % this "squeezes" the channel dimension out of the data
cfg.avgovertime = 'yes'; % this "squeezes" the time dimension out of the data
roiFIC = ft_selectdata(cfg, grandavgFIC);
roiFC = ft_selectdata(cfg, grandavgFC);
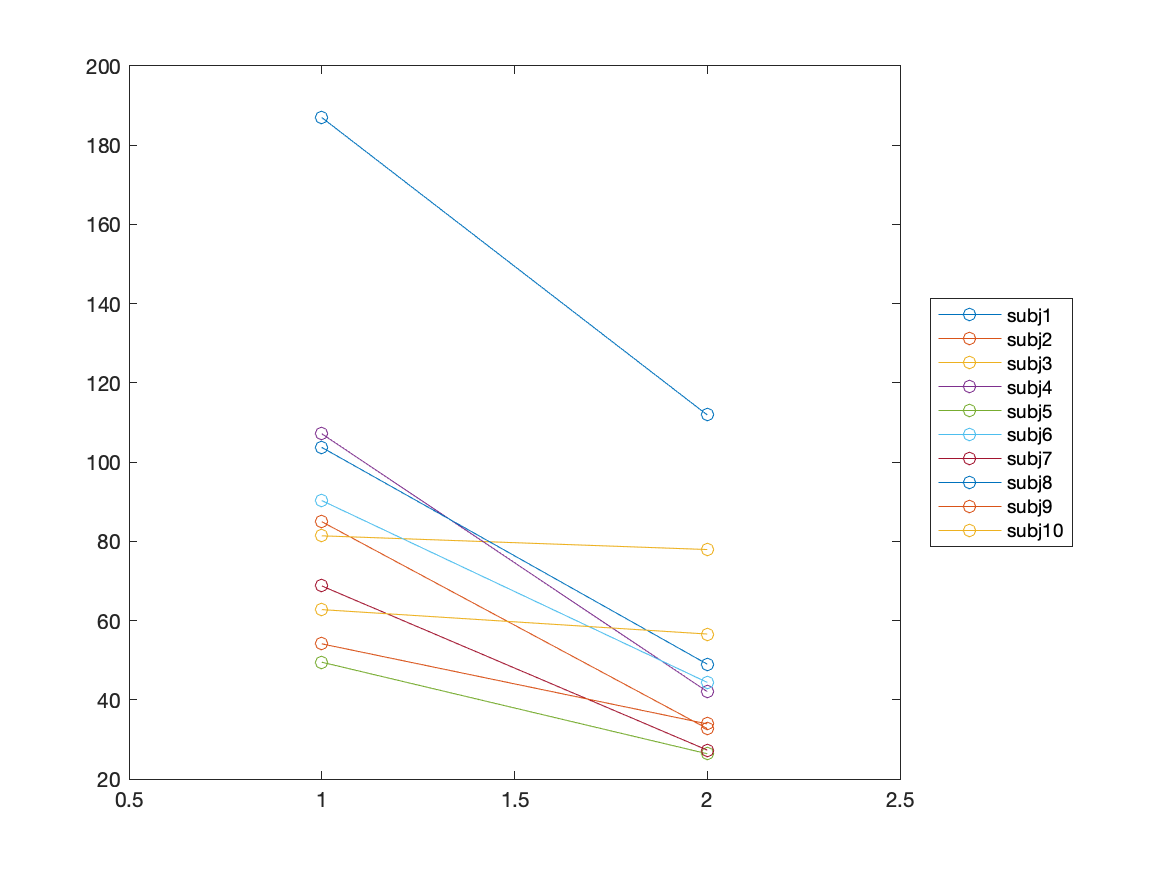
x1 = roiFIC.individual(:)*1e15; % express the data in fT
x2 = roiFC.individual(:)*1e15; % express the data in fT
n1 = length(x1);
n2 = length(x2);
figure; plot([x1 x2]', 'o-'); xlim([0.5 2.5])
legend({'subj1', 'subj2', 'subj3', 'subj4', 'subj5', 'subj6', ...
'subj7', 'subj8', 'subj9', 'subj10'}, 'location', 'EastOutside');
Computing the effect size by hand
Following the description of Cohen's d on Wikipedia we can quite easily compute the effect size as
pooled_sd = sqrt( ((n1-1)*std(x1)^2 + (n2-1)*std(x2)^2) / (n1+n2-1) );
cohensd = abs(mean(x1)-mean(x2)) / pooled_sd;
disp(cohensd)
1.1800
According to Sawilowsky, S (2009) as a rule of thumb these can be interpreted as follows.
| Qualitative | Quantitative |
|---|---|
| Very small | 0.01 |
| Small | 0.20 |
| Medium | 0.50 |
| Large | 0.80 |
| Very large | 1.20 |
| Huge | 2.00 |
The observed effect size of 1.18 can therefore be described as “large” to “very large”.
Computing the effect size using FieldTrip
Above we demonstrated how to compute it by hand. The same equation for Cohen's d is also implemented in FieldTrip and can be used like this:
cfg = [];
cfg.method = 'analytic';
cfg.statistic = 'cohensd'; % see FT_STATFUN_COHENSD
cfg.ivar = 1;
cfg.design = [
1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2
];
effect_roi_unpaired = ft_timelockstatistics(cfg, roiFIC, roiFC);
disp(effect_roi_unpaired)
stat: NaN
prob: NaN
cohensd: 1.1800
difference: 3.8744e-14
mask: 0
dimord: 'chan_time'
label: {'MLT12'}
time: 0.5000
cfg: [1x1 struct]
Note that Cohen's d is not the only way to quantify the effect size. If you look into the code of ft_statfun_cohensd, you will see that it is easy to implement other measures. You could also use a statfun to implement the Bayes factor to quantify the evidence of one hypothesis versus another.
Computing the paired effect size by hand
However, note that the computations demonstrated above are not the best way of testing, nor of reporting effect size: the experiment consists of a within-subject experimental manipulation and the observed data is “paired”. The appropriate way of computing the effect size therefore is to look at the within-subject differences:
cohensd = mean(x1-x2) ./ std(x1-x2);
disp(cohensd)
1.5811
This is larger than the previous estimate, part of the variance is explained by between-subject differences that are the same for both conditions.
The effect size is 1.58 after averaging in the time window from 300 to 700 milliseconds for a hand-picked channel (MLT12).
Computing the paired effect size using FieldTrip
Again, we can do the same computation with FieldTrip. For this we have to specify the unit of observation as cfg.uvar, which points to the 2nd row of the design matrix that contains the subject number.
cfg = [];
cfg.method = 'analytic';
cfg.statistic = 'cohensd'; % see FT_STATFUN_COHENSD
cfg.ivar = 1;
cfg.uvar = 2;
cfg.design = [
1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
];
effect_roi = ft_timelockstatistics(cfg, roiFIC, roiFC);
disp(effect_roi)
stat: NaN
prob: NaN
cohensd: 1.5811
difference: 3.8744e-14
mask: 0
dimord: 'chan_time'
label: {'MLT12'}
time: 0.5000
cfg: [1x1 struct]
Computing the maximum effect size
It is convenient to use FieldTrip for the channel and latency selection when computing the effect size, as we can make sub-selections. We can also compute it for all channels and time points in one go.
cfg = [];
cfg.parameter = 'individual';
cfg.channel = 'MEG';
cfg.method = 'analytic';
cfg.statistic = 'cohensd'; % see FT_STATFUN_COHENSD
cfg.ivar = 1;
cfg.uvar = 2;
cfg.design = [
1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
];
effect_all = ft_timelockstatistics(cfg, grandavgFIC, grandavgFC);
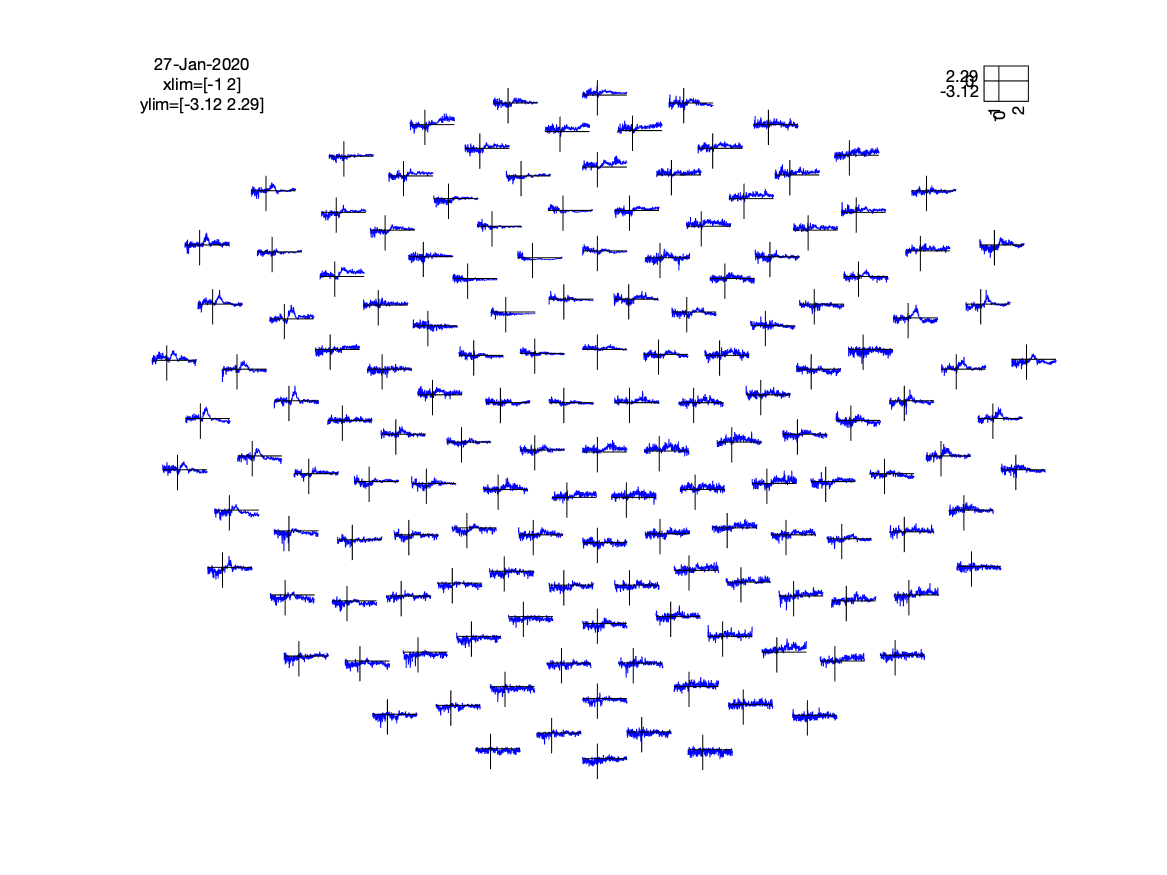
This results in a single effect size estimate for every MEG channel and for every timepoint. We can plot a distribution of the effect over all channels:
cfg = [];
cfg.layout = 'CTF151_helmet.mat';
cfg.parameter = 'cohensd';
ft_multiplotER(cfg, effect_all);
The channels with the largest effect are over the left temporal region, in line with the anticipated N400 effect. We can determine the channel and latency with the maximum effect like this:
[m, ind] = max(effect_all.cohensd(:));
[i, j] = ind2sub(size(effect_all.cohensd), ind);
fprintf('maximum effect of %g on channel %s at latency %g\n', effect_all.cohensd(i,j), effect_all.label{i}, effect_all.time(j));
maximum effect of 2.28609 on channel MLT13 at latency 0.406667
The maximum effect of 2.29 is observed on channel MLT13 at 407 milliseconds following stimulus onset.
Computing the effect size for an average over multiple channels
We can also compute the effect for an average of the data in a region of interest that consists of multiple channels and a specified time range:
cfg = [];
cfg.channel = {'MLT12', 'MLT13', 'MLT23', 'MLT24', 'MLT32', 'MLT33', 'MLT41'};
cfg.latency = [0.35 0.55];
cfg.avgoverchan = 'yes';
cfg.avgovertime = 'yes';
cfg.method = 'analytic';
cfg.statistic = 'cohensd'; % see FT_STATFUN_COHENSD
cfg.ivar = 1;
cfg.uvar = 2;
cfg.design = [
1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
];
effect_avg = ft_timelockstatistics(cfg, grandavgFIC, grandavgFC);
disp(effect_avg)
stat: NaN
prob: NaN
cohensd: 1.4708
difference: 3.1082e-14
mask: 0
dimord: 'chan_time'
label: {'mean(MLT12, MLT13, MLT23, MLT24, MLT32, MLT33, MLT41)'}
time: 0.4500
cfg: [1x1 struct]
The effect size is 1.47 when averaging over 7 left-temporal channels, and from 350 to 550 milliseconds.
Statistical inference using a cluster-based permutation test
Although we might have had a clear a priori hypothesis for the timing of the N400 effect on the basis of previous ERP research, we actually do not have such a clear expectations for the MEG channels on which the effect will show. Hence - rather than picking channels following visual inspection - the correct procedure is to test for the hypothesized effect on all channels, dealing with multiple comparison correction. Please see the Cluster-based permutation tests on event-related fields tutorial for more details.
% define neighbouring channels
load ctf151_neighb.mat
cfg = [];
cfg.method = 'montecarlo';
cfg.statistic = 'ft_statfun_depsamplesT';
cfg.channel = 'MEG';
cfg.latency = [0.3 0.7];
cfg.avgovertime = 'no';
cfg.alpha = 0.05;
cfg.numrandomization = 'all';
cfg.neighbours = neighbours; % from the mat file
cfg.minnbchan = 2; % minimal neighbouring channels
cfg.correctm = 'cluster';
cfg.correcttail = 'prob';
cfg.spmversion = 'spm12';
cfg.ivar = 1; % the 1st row in cfg.design contains the independent variable
cfg.uvar = 2; % the 2nd row in cfg.design contains the subject number
cfg.design = [
1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
];
cfg.parameter = 'avg';
inference = ft_timelockstatistics(cfg, allsubjFIC{:}, allsubjFC{:});
Using this approach, we see that the null-hypothesis (H0) of the data being exchangeable between conditions is very unlikely, and therefore we reject it in favor of the alternative hypothesis (H1), which states that the data is different between conditions.
The probability is returned for each channel-time point as a matrix; which can be plotted like this:
figure
imagesc(inference.time, 1:151, -log10(inference.prob))
colorbar
A p-value of 10% corresponds here to a -log10() value of 1, a p-value of 1% corresponds to 2. The critical threshold is at 5%, which corresponds to a value of 1.3 in this figure. There is one cluster displayed in yellow with a p-value smaller than 5%.
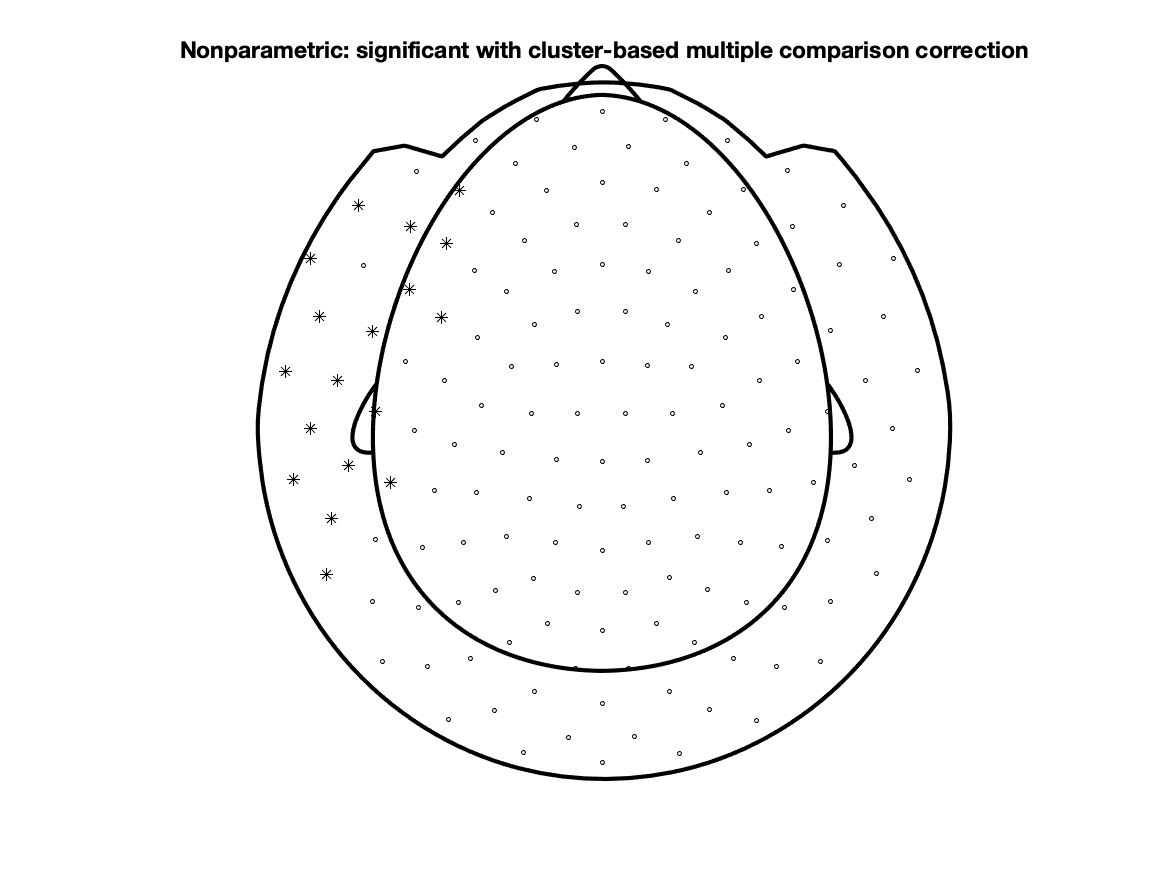
We can also make a plot of the spatial distribution of MEG channels that are part of the largest cluster:
cfg = [];
cfg.style = 'blank';
cfg.layout = 'CTF151_helmet.mat';
cfg.highlight = 'on';
cfg.highlightchannel = find(any(inference.mask,2));
cfg.comment = 'no';
figure; ft_topoplotER(cfg, grandavgFIC)
title('Nonparametric: significant with cluster-based multiple comparison correction')
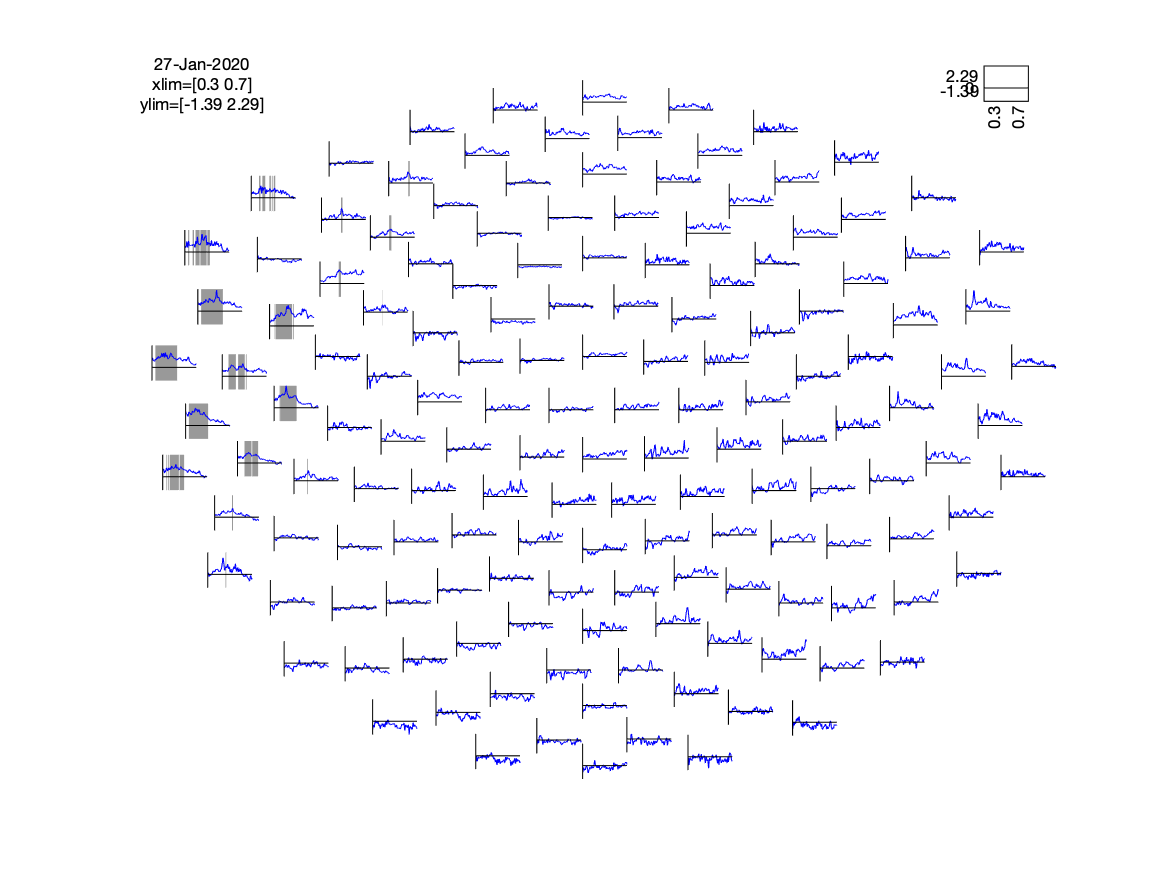
We can also combine the statistical mask - which corresponds to the clusters that are unlikely given the permutation distribution - with the estimated effect size and plot them together:
cfg = [];
cfg.channel = 'MEG';
cfg.latency = [0.3 0.7];
effect_with_mask = ft_selectdata(cfg, effect_all);
effect_with_mask.mask = inference.mask;
cfg = [];
cfg.layout = 'CTF151_helmet.mat';
cfg.parameter = 'cohensd';
cfg.maskparameter = 'mask';
ft_multiplotER(cfg, effect_with_mask);
The cluster on the basis of which H0 was rejected does not have a nice rectangular shape, i.e. some channels are part of the cluster for a longer time, some for a shorter time, and some of them are only on and off part of the cluster.
Computing the effect size for the average over the cluster
We can select and average the data in the cluster for both conditions in each of our participants:
% first make the same selection as used in the inferential statistics
cfg = [];
cfg.channel = 'MEG';
cfg.latency = [0.300 0.700];
grandavgFIC_sel = ft_selectdata(cfg, grandavgFIC);
grandavgFC_sel = ft_selectdata(cfg, grandavgFC);
x1 = nan(10,1);
x2 = nan(10,1);
for i=1:10
% construct a 3-dimensional Boolean array to select the data from this participant
sel3d = false(size(grandavgFIC_sel.individual));
sel3d(i,:,:) = inference.mask;
% select the FIC data in the cluster for this participant, represent it as a vector
tmp = grandavgFIC_sel.individual(sel3d(:));
% compute the average over the cluster
x1(i) = mean(tmp);
% select the FC data in the cluster for this participant, represent it as a vector
tmp = grandavgFC_sel.individual(sel3d(:));
% compute the average over the cluster
x2(i) = mean(tmp);
end
n1 = length(x1);
n2 = length(x2);
figure; plot([x1 x2]', 'o-'); xlim([0.5 2.5])
legend({'subj1', 'subj2', 'subj3', 'subj4', 'subj5', 'subj6', ...
'subj7', 'subj8', 'subj9', 'subj10'}, 'location', 'EastOutside');
title('individual scores, averaged over cluster');
Comparing this to the initial hand-picked channel, we can see that the effect is slightly “steeper” and more consistent over all subjects.
And again we can compute the effect size:
cohensd = mean(x1-x2) ./ std(x1-x2);
disp(cohensd)
1.7369
When averaging the data over the largest cluster, i.e. the one on the basis of which we rejected H0, we see that the estimated effect size is 1.74.
Which effect size to report?
We have demonstrated that there are different ways to estimate the effect size.
- effect size for a hand-picked single channel (1.58)
- maximum effect over all channels and latencies (2.29)
- effect size for an average over multiple channels (1.47)
- effect size for an average over the cluster (1.74)
Neither of these estimates is per se correct or incorrect; the one to report depends on what you expect the readers of your manuscript to do with it. For example, if you expect your readers to do a follow up experiment with precisely the same experimental setup, i.e., the same EEG or MEG system (although for MEG it will be unlikely that the subjects will be seated exactly the same), then you can report the value at one specific channel. If your readers want to follow up with a system that for example has fewer channels (say 19 channels instead of 64), the effect size averaged over multiple channels might be more informative for them as they can pick a channel in their system that falls within the group that you averaged.
The maximum effect can unambiguously be determined over all observations, but will always be positively biased. If the data preprocessing would have been done slightly different (e.g., different filter settings), the maximum effect size might already be quite different.
The effect size after averaging the data in the largest cluster is the one that most closely relates to the statistical inference that was done here using a cluster-based permutation test. However, it is very difficult to report the precise details of the cluster due to its ragged shape. Furthermore, there is no reason to assume that exactly the same cluster would be found in a follow-up study with independent data; although we would expect a similar effect, the edges of the cluster and its extend would be different.
More important perhaps is to consider the effect that the cluster-forming-threshold (the cfg.clusterthreshold option in ft_statistics_montecarlo, for which we used the default here) would have on the effect size. If the cluster threshold is higher, the cluster would have a smaller spatial and temporal extent and would only contain the peak, hence the effect within that cluster would be larger. With a lower cluster threshold, the cluster would be larger, and the effect computed over the average in the cluster would be smaller. The cluster threshold has a complex relationship to the statistical sensitivity of the test and to the effect size for the average over the resulting cluster. Note that in a hypothesis-driven study you should not use the cluster threshold to “optimize” (or p-hack) your statistical inference.
Average over the circumscribed rectangle
Another way of computing and reporting the effect size following a cluster-based test is to determine the circumscribed square area that spans the cluster, i.e. a rectangle (in channels and time and/or frequency) that fits tightly around the cluster. See also https://en.wikipedia.org/wiki/Circumscribed_circle for an explanation. This can be computed by converting the Boolean mask into a logical row-vector and finding the minimum and maximum corresponding time points like this:
min(inference.time(any(inference.mask,1)))
ans =
0.3300
max(inference.time(any(inference.mask,1)))
ans =
0.5267
For the channels it is similar, except that we form a Boolean column-vector to find all channels that are part of the cluster at any given time.
inference.label(any(inference.mask,2))
ans =
18x1 cell array
{'MLF23'}
{'MLF33'}
{'MLF34'}
{'MLF44'}
{'MLT11'}
{'MLT12'}
{'MLT13'}
{'MLT14'}
{'MLT23'}
{'MLT24'}
{'MLT31'}
{'MLT32'}
{'MLT33'}
{'MLT34'}
{'MLT41'}
{'MLT42'}
{'MLT43'}
{'MLT44'}
The advantage of the list of channels and the begin- and end-latency is that these are easy to report in a written manuscript/paper. As before, these can be used to compute the average in the region of interest, and to compute the effect size for that rectangle:
cfg = [];
cfg.channel = inference.label(any(inference.mask,2));
cfg.latency = [min(inference.time(any(inference.mask,1))) max(inference.time(any(inference.mask,1)))];
cfg.avgoverchan = 'yes';
cfg.avgovertime = 'yes';
cfg.method = 'analytic';
cfg.statistic = 'cohensd'; % see FT_STATFUN_COHENSD
cfg.ivar = 1;
cfg.uvar = 2;
cfg.design = [
1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
];
effect_rectangle = ft_timelockstatistics(cfg, grandavgFIC, grandavgFC);
disp(effect_rectangle)
stat: NaN
prob: NaN
cohensd: 1.4356
difference: 1.9677e-14
mask: 0
dimord: 'chan_time'
label: {'mean(MLF23, MLF33, MLF34, MLF44, MLT11, MLT12, MLT13, MLT14, MLT23, MLT24, MLT31, MLT32, MLT33, MLT34, MLT41, MLT42, MLT43, MLT44)'}
time: 0.4283
cfg: [1x1 struct]
The effect size for the data averaged in the circumscribed rectangle is 1.43.
Summary
Following some discussion in the MEG lab meeting at the Donders Centre for Cognitive Neuroimaging (DCCN), we think that both the effect size for the circumscribed rectangle and the size of the maximum effect are interesting to report. Usually the first will give a conservative lower bound on the effect size, whereas the second gives an upper bound on the effect size. Furthermore, for both it is easy to report the area or location (in channels and time and/or frequency).
Regardless of how you compute the effect size that you report: as long as you compute and report the effect size, plus some details that help the reader interpret the effect size and use it in building upon your work, you are contributing to making science better and more reproducible!
See also
- There is an interesting crowdsourced document on Effect size, confidence intervals, and power analyses with practical guidance
- Other pages on this website that are tagged with statistics