Solving the EEG inverse problem
Introduction
In this tutorial you can find information about how to fit dipole models and how to do source reconstruction using minimum-norm estimation to the somatosensory evoked potentials (SEPs) of a single subject from the preprocessing.
We will be working on the dataset from the previous hands on sessions, and we will use the functional and anatomical data from these tutorials to deal with the inverse problem. As you already noticed we have prepared two different mathematical models from the forward problem. We will use both to solve the inverse problem and compare the results. You’ve either got the relevant data already processed yourself or can find in the data directory.
This tutorial will not show how to combine source-level data over multiple subjects. It will also not describe how to do source-localization of oscillatory activation. You can check the Localizing oscillatory sources using beamformer techniques tutorial if you are interested in the later.
Background
Dipole fit
In this tutorial we will use the dipole fitting approach (1) to localise the neuronal activity and (2) to estimate the time course of the activity. This approach is most suitable for relatively early cortical activity which is not spread over many or large cortical areas. Dipole fitting assumes that a small number of point-like equivalent current dipoles (ECDs) can describe the measured topography. It optimises the location, the orientation and the amplitude of the model dipoles in order to minimise the difference between the model and measured topography. A good introduction to dipole fitting is provided by Scherg in Fundamentals of dipole source potential analysis.
Minimum norm estimate
To calculate distributed neuronal activation we will use the minimum-norm estimation. This approach is favored for analyzing evoked responses and for tracking the wide-spread activation over time. It is a distributed inverse solution that discretizes the source space into locations on the cortical surface or in the brain volume using a large number of equivalent current dipoles. It estimates the amplitude of all modeled source locations simultaneously and recovers a source distribution with minimum overall energy that produces data consistent with the measurement (Ou, W., Hämäläinen, M., Golland, P., 2008, A Distributed Spatio-temporal EEG/MEG Inverse Solver. Jensen, O., Hesse, C., 2010, Estimating distributed representation of evoked responses and oscillatory brain activity, In: MEG: An Introduction to Methods, ed. by Hansen, P., Kringelbach, M., Salmelin, R., doi:10.1093/acprof:oso/9780195307238.001.0001). The reference for the implemented method is Dale et al. (2000).
Dipole fit
For this tutorial you should have already computed everything need in advance.
load elec
load headmodel_fem_eeg_tr
load leadfield_fem_eeg
load mri_resliced
load EEG_avg
load MEG_avg
load mesh_surf
If you can use duneuro you should already computed this files. If not you can load them here.
load leadfield_fem_meg
EEG
We start with a grid search. In our case, this should be enough. The resolution of the source model is fine enough so that a further nonlinear fitting is not necessary.
% Dipole fit
cfg = [];
cfg.numdipoles = 1; % number of expected
cfg.headmodel = headmodel_fem_eeg_tr; % the head model
cfg.grid = leadfield_fem_eeg; % the precomputed leadfield
cfg.nonlinear = 'no'; % only dipole scan
cfg.elec = elec; % the electrode model
cfg.latency = 0.025; % the latency of interest
dipfit_fem_eeg = ft_dipolefitting(cfg,EEG_avg);
A quick look dipfit_bem.dip gives us information about the dipole fit. Especially a low residual variance (rv) shows us that the fitted dipole quite well explains the data.
disp(dipfit_fem_eeg.dip)
ans =
pos: [10 26 90] % dipole position
mom: [3x1 double] % dipole moment
pot: [74x1 double] % potential at the electrodes
rv: 0.027147418310096 % residual variance
unit: 'mm'
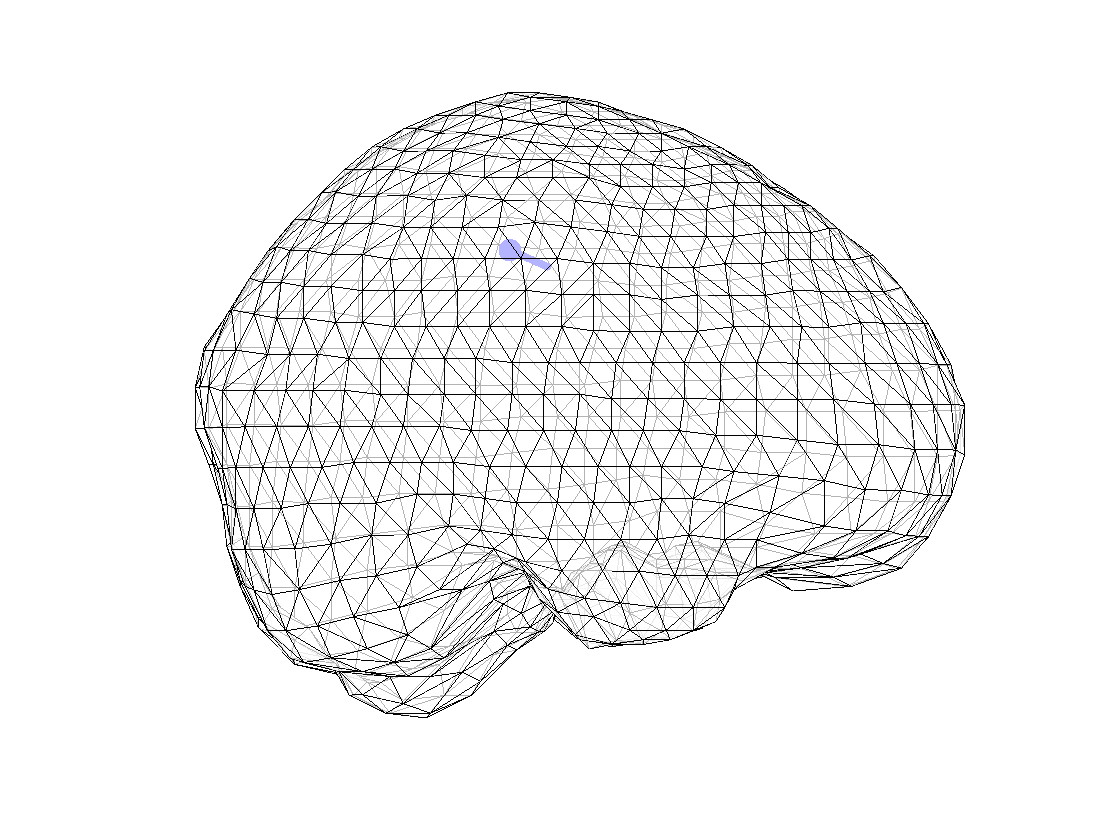
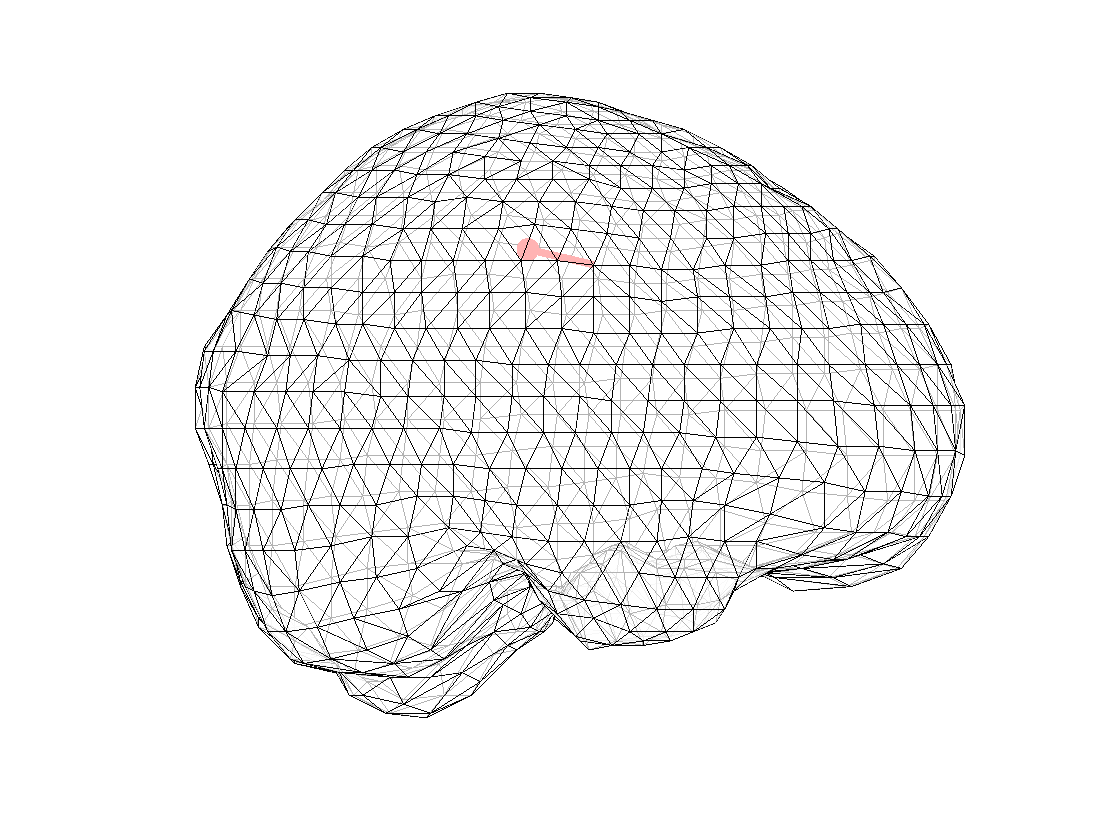
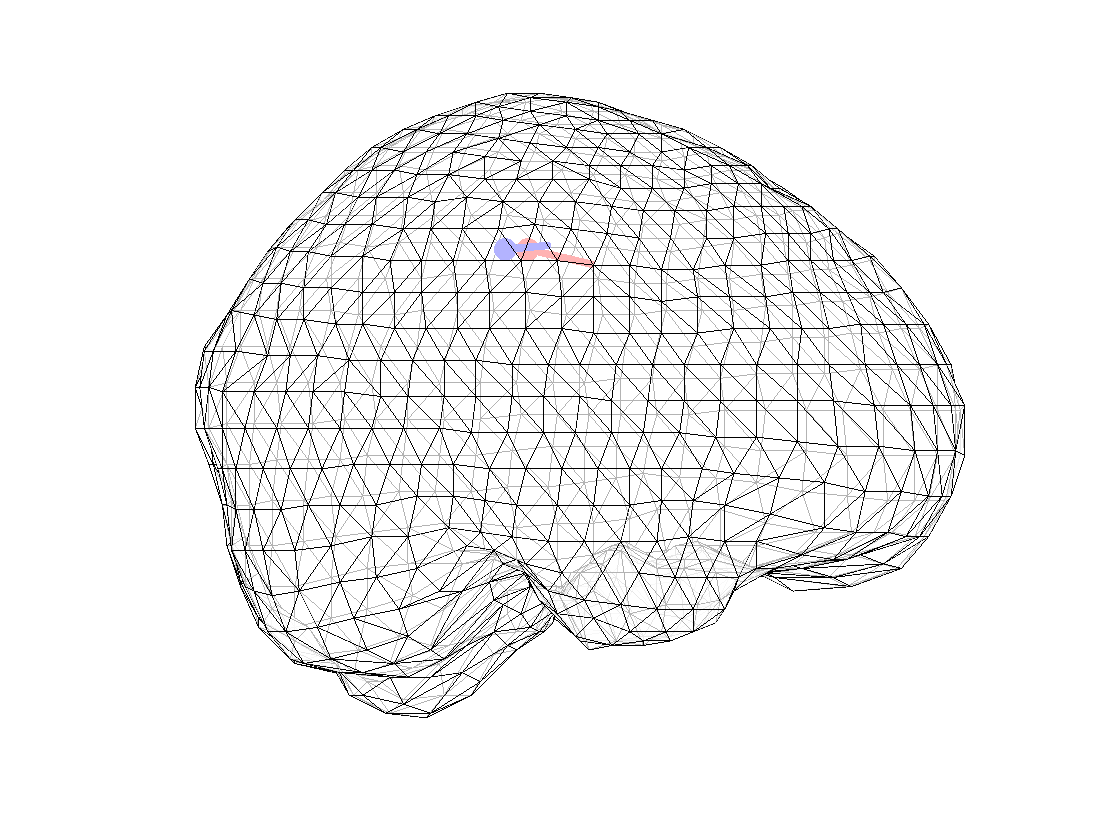
And we visualize the dipole and see where it was localized in the brain.
% Visualise dipole fit
ft_plot_mesh(mesh_surf(3));
alpha 0.7;
ft_plot_dipole(dipfit_fem_eeg.dip.pos(1,:), mean(dipfit_fem_eeg.dip.mom(1:3,:),2), 'color', 'b', 'unit', 'mm')
Figure 1. Dipole computed with FEM model for EEG
MEG
Now we do a grid search with MEG.
Be aware that this step only works, if you can use Duneuro. Otherwise just load dipfit_fem_meg and skip ft_dipolefitting.
% Dipole fit
cfg = [];
cfg.numdipoles = 1; % number of expected
cfg.headmodel = headmodel_fem_meg_tr; % the head model
cfg.grid = leadfield_fem_meg; % the precomputed leadfield
cfg.nonlinear = 'no'; % only dipole scan
cfg.grad = grad; % the electrode model
cfg.latency = 0.025; % the latency of interest
dipfit_fem_meg = ft_dipolefitting(cfg, MEG_avg);
Again we look at dipfit_bem.dip to see the information about the reconstructed dipole. The residual variance again is very low.
disp(dipfit_fem_meg.dip)
ans =
pos: [14 52 90] % dipole position
mom: [3x1 double] % dipole moment
pot: [271x1 double] % potential at the electrodes
rv: 0.023526877979900 % residual variance
unit: 'mm'
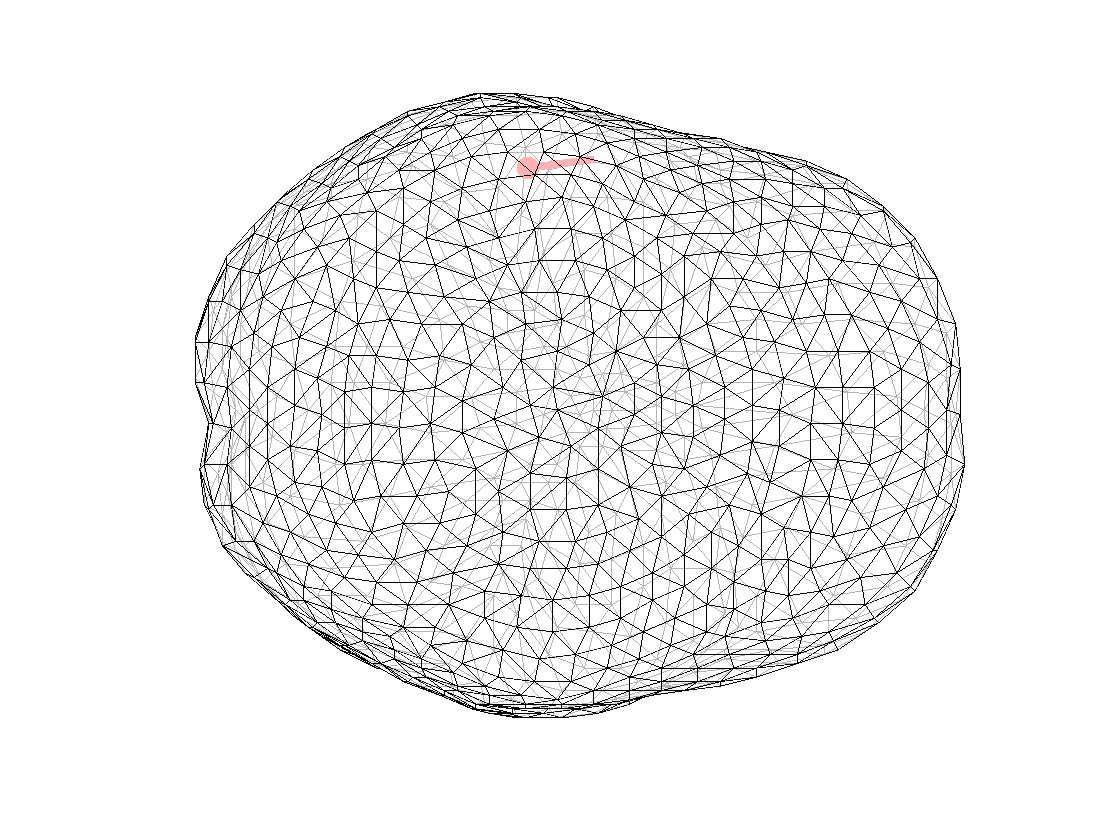
And we visualize the dipole and see where it was localized in the brain.
% Visualise dipole fit
ft_plot_mesh(mesh_surf(3));
alpha 0.7;
ft_plot_dipole(dipfit_fem_meg.dip.pos(1,:), mean(dipfit_fem_meg.dip.mom(1:3,:),2), 'color', 'r', 'unit', 'mm')
Figure 2. Dipole computed with FEM model for MEG
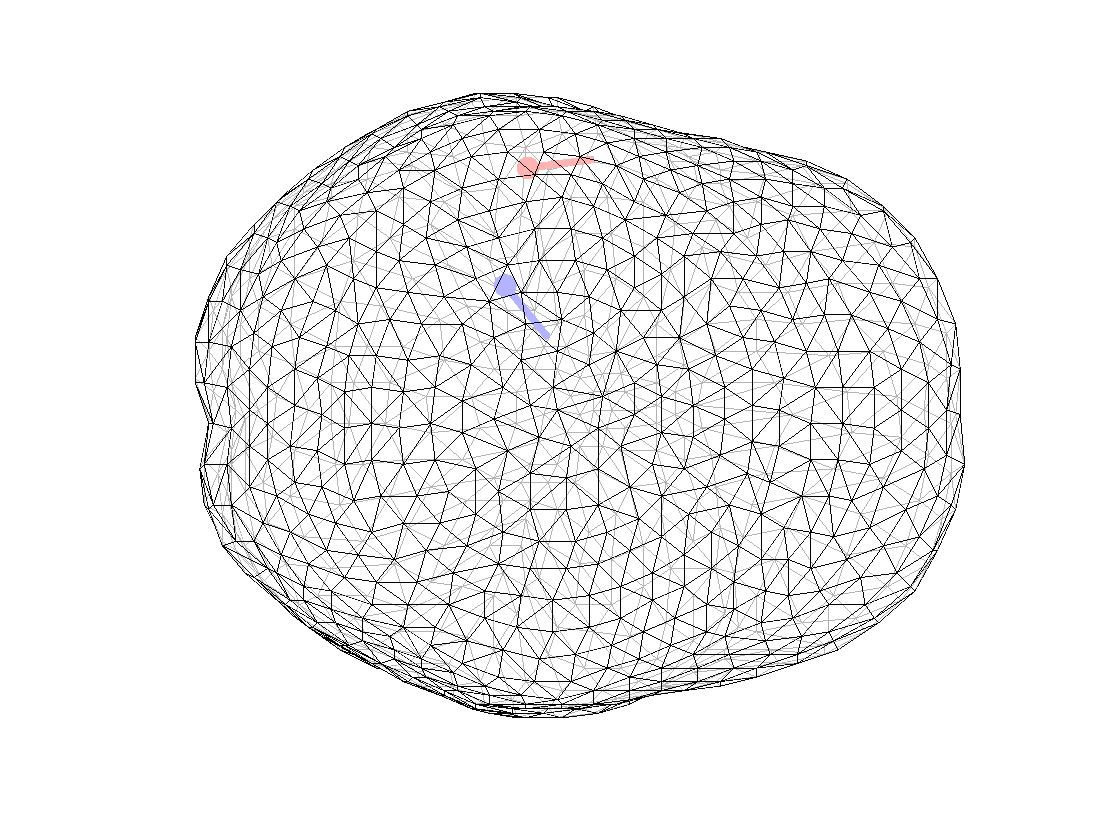
Comparison of EEG and MEG
ft_plot_mesh(mesh_surf(3));alpha 0.7;
ft_plot_dipole(dipfit_fem_eeg.dip.pos(1,:), mean(dipfit_fem_eeg.dip.mom(1:3,:),2), 'color', 'b', 'unit', 'mm')
ft_plot_dipole(dipfit_fem_meg.dip.pos(1,:), mean(dipfit_fem_meg.dip.mom(1:3,:),2), 'color', 'r', 'unit', 'mm')
Minimum norm estimate
EEG
We now start with a MNE in EEG.
cfg = [];
cfg.method = 'mne'; % specify minimum norm estimate as method
cfg.latency = 0.025; % latency of interest
cfg.grid = leadfield_fem_eeg; % the precomputed leadfield
cfg.headmodel = headmodel_fem_eeg_tr; % the head model
cfg.mne.prewhiten = 'yes'; % prewhiten data
cfg.mne.lambda = 0.1; % regularisation parameter
cfg.mne.scalesourcecov = 'yes'; % scaling the source covariance matrix
minimum_norm_eeg = ft_sourceanalysis(cfg, EEG_avg);
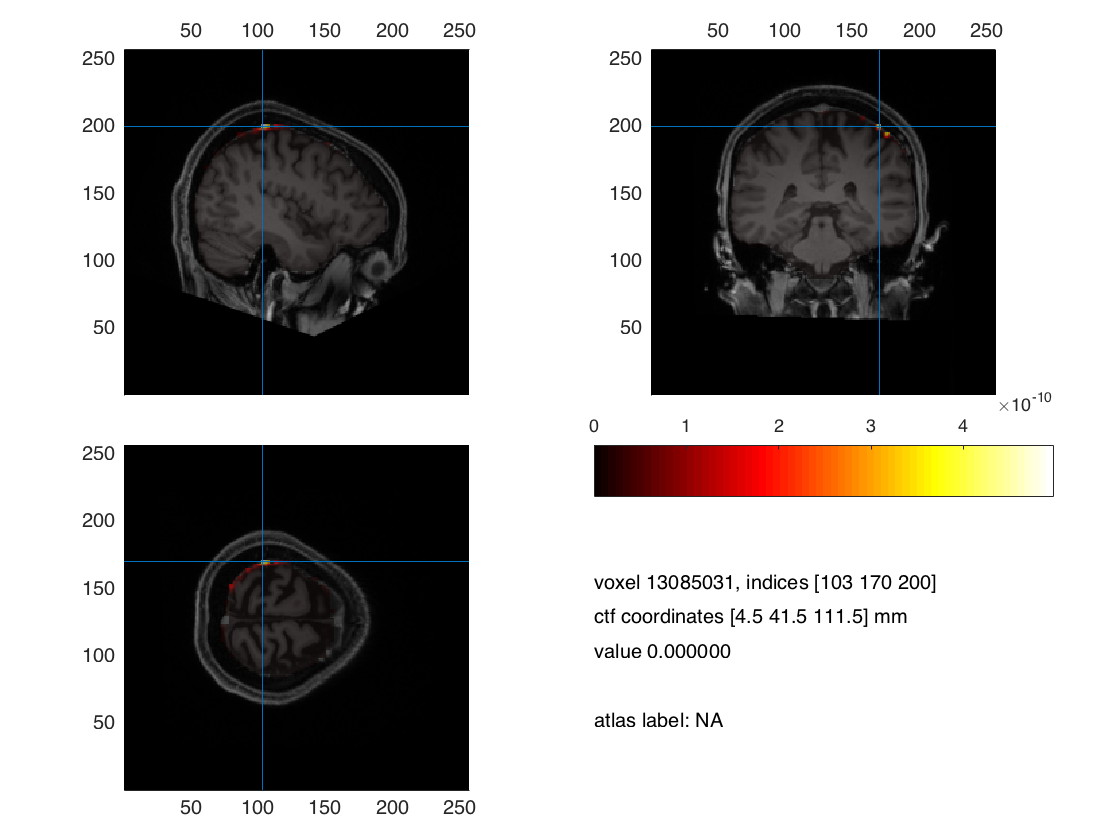
For the purpose of visualization, we interpolate the MNE results onto the replaced anatomical MRI.
cfg = [];
cfg.parameter = 'avg.pow';
interpolate = ft_sourceinterpolate(cfg, minimum_norm_eeg , mri_resliced);
cfg = [];
cfg.method = 'ortho';
cfg.funparameter = 'pow';
ft_sourceplot(cfg,interpolate);
Figure 3. Minimum norm estimation with FEM model for EEG
MEG
cfg = [];
cfg.method = 'mne'; % specify minimum norm estimate as method
cfg.latency = 0.025; % latency of interest
cfg.grid = leadfield_fem_meg; % the precomputed leadfield
cfg.headmodel = headmodel_fem_meg_tr; % the head model
cfg.mne.prewhiten = 'yes'; % prewhiten data
cfg.mne.lambda = 0.1; % regularisation parameter
cfg.mne.scalesourcecov = 'yes'; % scaling the source covariance matrix
minimum_norm_meg = ft_sourceanalysis(cfg, MEG_avg);
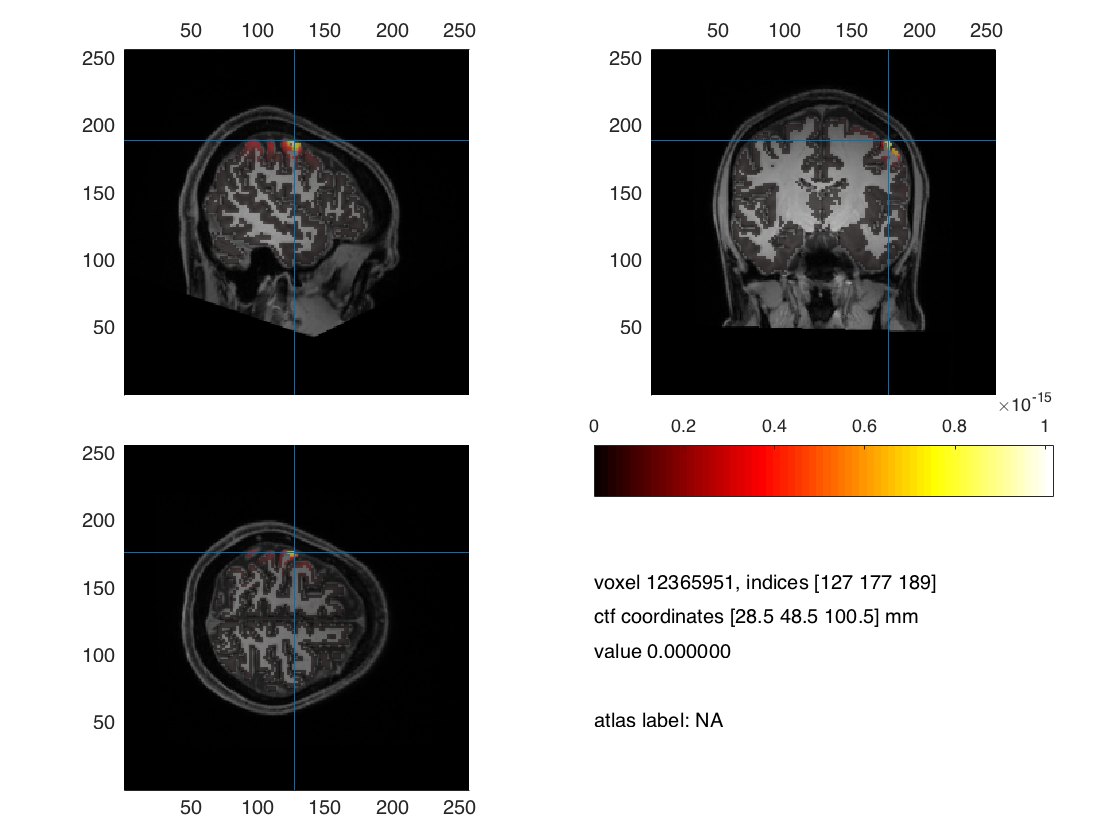
For the purpose of visualization, we interpolate the MNE results onto the replaced anatomical MRI.
cfg = [];
cfg.parameter = 'avg.pow';
interpolate = ft_sourceinterpolate(cfg, minimum_norm_meg, mri_resliced);
cfg = [];
cfg.method = 'ortho';
cfg.funparameter = 'pow';
ft_sourceplot(cfg,interpolate);
Figure 4. Minimum norm estimation with FEM model for MEG
Exercises
Exercise 1
Can you think of reasons why the dipoles are at different locations?
Exercise 2
You can play around with cfg.mne.lambda? Do you see the influence of different lambdas on the MNE solution?
Exercise 3
You can also play around with other parameters for the MNE. To find out more about MNE just type “help minimumnormestimate” into Matlab
Exercise 4
Changing parameters of the forward model influences the Inverse solutions. Play around with different parameters of the FEM forward model (e.g., changing conductivity values, move electrodes or play around with the segmentation) and redo the inverse solution. If you need more input for this please ask us!
Summary and suggested further reading
In this tutorial, we learned how to solve the inverse problem. For this, we used the preprocessed functional data and the forward model. The inverse techniques we used in this tutorial were “Dipole Fit” and “Minimum Norm Estimation”. We used both techniques with the different parameters for EEG and MEG.
Here are some related FAQs
- Can I compare EEG channels between different electrode caps?
- How should I specify the fiducials for electrode realignment?
- How are electrodes, magnetometers or gradiometers described?
- How can I inspect the electrode impedances of my data?
- How should I report the positions of the fiducial points on the head?
- Should I use a Polhemus or a Structure Sensor to record electrode positions?
- Can I do combined EEG and MEG source reconstruction?
- How is the segmentation defined?
- How to coregister an anatomical MRI with the gradiometer or electrode positions?
and some related examples:
- Combined EEG and MEG source reconstruction
- Compute forward simulated data using ft_dipolesimulation
- Compute forward simulated data with the low-level ft_compute_leadfield
- Align EEG electrode positions to BEM headmodel
- Compute EEG leadfields using a FEM headmodel
- Testing BEM created EEG lead fields
and other tutorials