Simulate an oscillatory signal with phase resetting
Narrow-band oscillation
The following code simulates a clean oscillating signal with a phase reset at time zero.
clear all
close all
f = 5;
t = (-1000:1:1000)/1000;
figure
for i=1:10 % repeat 10 times
s = nan(size(t));
s(t<0 ) = cos(2*pi*f*t(t<0 ) + 2*pi*rand(1)); % random phase
s(t>=0) = cos(2*pi*f*t(t>=0) ); % constant phase
s = 0.2*s+i;
d(i,:) = s; % remember the signal on each repetition
plot(t, s);
hold on;
end
axis auto
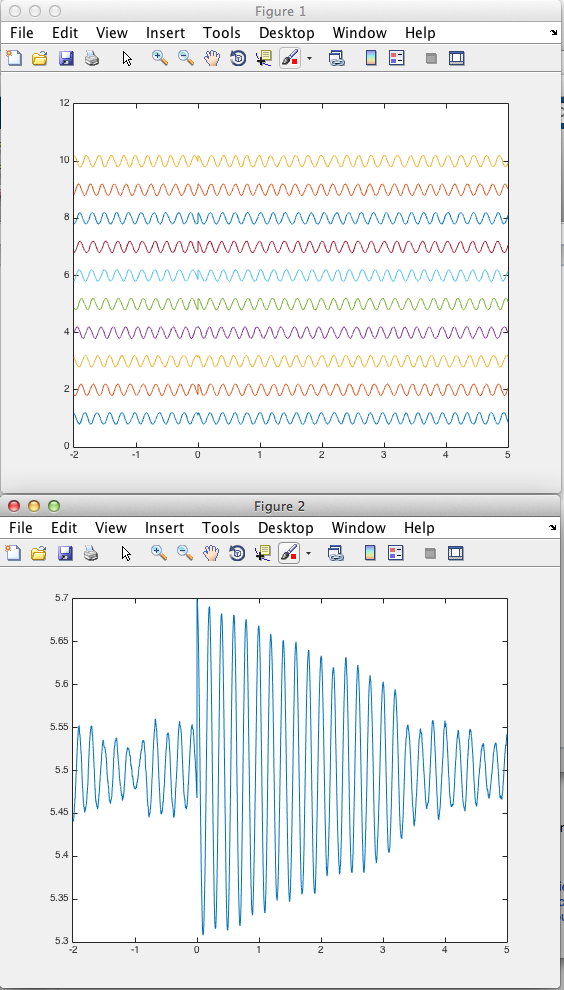
figure;
plot(t, mean(d,1))
Broad-band oscillation
The following code also includes a small “random walk” in the phase, i.e. the signal is a little bit broad-band and over time there is some phase dispersion. At t=0 there is still a phase reset. The phase dispersion causes the average ERF again to disappear some time following the phase reset.
clear all
close all
f = 5;
t = (-2000:1:5000)/1000;
figure
for i=1:10 % repeat 10 times
p = 2*pi*f*t; % linear phase increase
p(t<0) = p(t<0) + 2*pi*rand(1); % random phase prior to TMS pulse
p = p + cumsum(2*pi*(rand(size(p))-0.5)*0.01); % random walk
p = p - p(t==0);
s = cos(p);
s = 0.2*s+i;
d(i,:) = s; % remember the signal on each repetition
plot(t, s);
hold on;
end
axis auto
figure;
plot(t, mean(d,1))