How can I fine-tune my BEM volume conduction model?
The construction of a BEM volume conduction model is not always straight forward, especially if the quality of the MRI is not optimal or if the model needs to be very accurate. For example, getting an accurate estimate of the thickness of the skull or incorporating the CSF layer is difficult.
The strategy employed in FieldTrip for constructing the BEM model boils down to the manipulation of geometrical data. The following qualitatively different classes of data are distinguished:
- anatomical MRI, described as voxels in a regular 3-D lattice, grey values
- segmented MRI, described as voxels in a regular 3-D lattice, boolean or probabilistic values
- mesh, consisting of vertices and elements (triangles, tetrahedra, hexahedra)
In case of the BEM, the volume conduction model consists of one or multiple homogenous and isotropic compartments. The compartment boundaries are closed and non-intersecting surfaces that are described by triangulated meshes. Furthermore, each of the compartments is described by a conductivity.
To make the highest quality BEM volume conduction model, FieldTrip offers a number of functions to manipulate these three classes of geometrical data. If we summarize the geometrical data as anatomy, segmentation and mesh, then we can consider functions that take one type of geometrical data as input, and return the same or another type.
We will refrain from using “head model” in the subsequent explanation, since each of the representations can be thought of as a “model describing the head”.
Converting anatomy to anatomy
Converting anatomy to segmentation
Converting segmentation to segmentation
Here it helps to distinguish the different representations. Examples of these are given in ft_datatype_segmentation.
- probabilistic, also known as tissue probability map (tpm): there is a value between 0 and 1 for each tissue at each of the voxels. This requires each tissue to be described in a separate 3-D array.
- indexed: the segmentation serves as a look-up table, each voxel is assigned to one class of tissue. This requires a set of labels for each tissue type.
The probabilistic representation can also be used to make a binary or boolean representation, i.e. one in which the probability is either 0% (false) or 100% (true).
Inside ft_prepare_mesh there are some helper functions that do some sanity checks on the segmentation and that can convert one representation to another.
The MATLAB image processing toolbox includes a number of morphological operations that are very useful for manipulating binary segmentations. Some of the most common operators are imfill, imdilate, bwlabeln, etc.
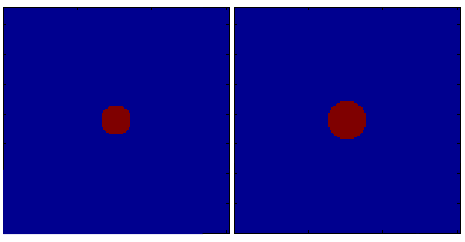
In particular imdilate can be used to augment the volume of a closed surface (e.g., the inner skull) in order to render the other surrounding tissues (e.g., the outer skull). An example is shown below:
The code used to generate the figure is:
seg = imdilate(seg,strel_bol(3));
figure
volplot(seg);
An example of the imfill function is given below. This is the case, for example, in which we want to fill the volume so that it constitutes a single entity. It results in being useful for triangulation, as explained in one of the techniques to obtain the outer-most surface (i.e. the skin).
The code used to generate the figure is:
seg = imfill(seg,'holes');
figure
volplot(seg);
The same effect can be reached with the use of another morphology function: bwlabeln. This function classifies the cluster of neighboring voxels and attaches a label to them, so that different objects can be easily distinguished (and processed) in the successive steps.
Converting anatomy to mesh
The ft_prepare_mesh function allows you to interactively make a mesh, i.e. by manually clicking in an anatomical MRI, by specifying cfg.method=’interactive’. It will give you a simple user interface that allows you to add and remove points in each of the slices. The vertices in each of the slices are connected together to form a closed triangulated mesh.
Converting segmentation to mesh
The ft_prepare_mesh function has the ‘projectmesh’, ‘iso2mesh’ and ‘isosurface’ methods for constructing a mesh from a segmentation.
The projectmesh method works by projecting lines from the center of an icosahedron or other nice spherical mesh through the vertices, to obtain the points of the volume that correspond to the transition between inside (true) and outside (false of the binary volume. The resulting surface is closed and topologically equivalent to a sphere. However, the triangles are not uniformly sized over the whole surface.
The isosurface method corresponds to the marching cubes algorithm implemented by the MATLAB isosurface.m function. This results in a very detailed description of the surface. The level of detail is typically too large for BEM, making it computationally too slow. Furthermore, the resulting mesh is not guaranteed to be closed (i.e. topologically equivalent to a sphere).
The iso2mesh method uses the vol2surf function from the iso2mesh toolbox.
Converting mesh to mesh
The iso2mesh toolbox includes very useful functions for mesh manipulations.
Also SPM includes functions for triangular mesh manipulation:
- spm_mesh_adjacency.m
- spm_mesh_clusters.m
- spm_mesh_curvature.m
- spm_mesh_distmtx.m
- spm_mesh_get_lm.m
- spm_mesh_inflate.m
- spm_mesh_label.m
- spm_mesh_normals.m
- spm_mesh_project.m
- spm_mesh_render.m
Converting mesh to volume conduction model
The ft_prepare_headmodel function can take a single or the combination of multiple meshes as input and make a volume conduction model out of it. This construction of the volume conduction model can for example consist of fitting spheres to the mesh for a concentric sphere model, or the computation of a BEM system matrix.
After constructing the volume conduction model of the head, FieldTrip can compute leadfields and estimate sources by solving the inverse problem. Please see the tutorial documentation for complete examples.