Solving the EEG and MEG forward problem using the finite element method
Introduction
The aim of this tutorial is to solve the EEG and MEG forward problems using the Finite Element Method (FEM).
Background
The EEG/MEG signals measured on or around the scalp do not directly reflect the activated neurons in the brain. To reconstruct the actual activity in the brain, source reconstruction techniques are used. You can read more about the different methods in the review papers that are listed here.
The activity in the brain is estimated from the EEG or MEG signals using
- the EEG/MEG activity itself that is measured on or around the scalp
- the spatial arrangement of the electrodes/gradiometers relative to the brain (sensor positions),
- the geometrical and conductive properties of the head (head model)
- the location of the source (source model)
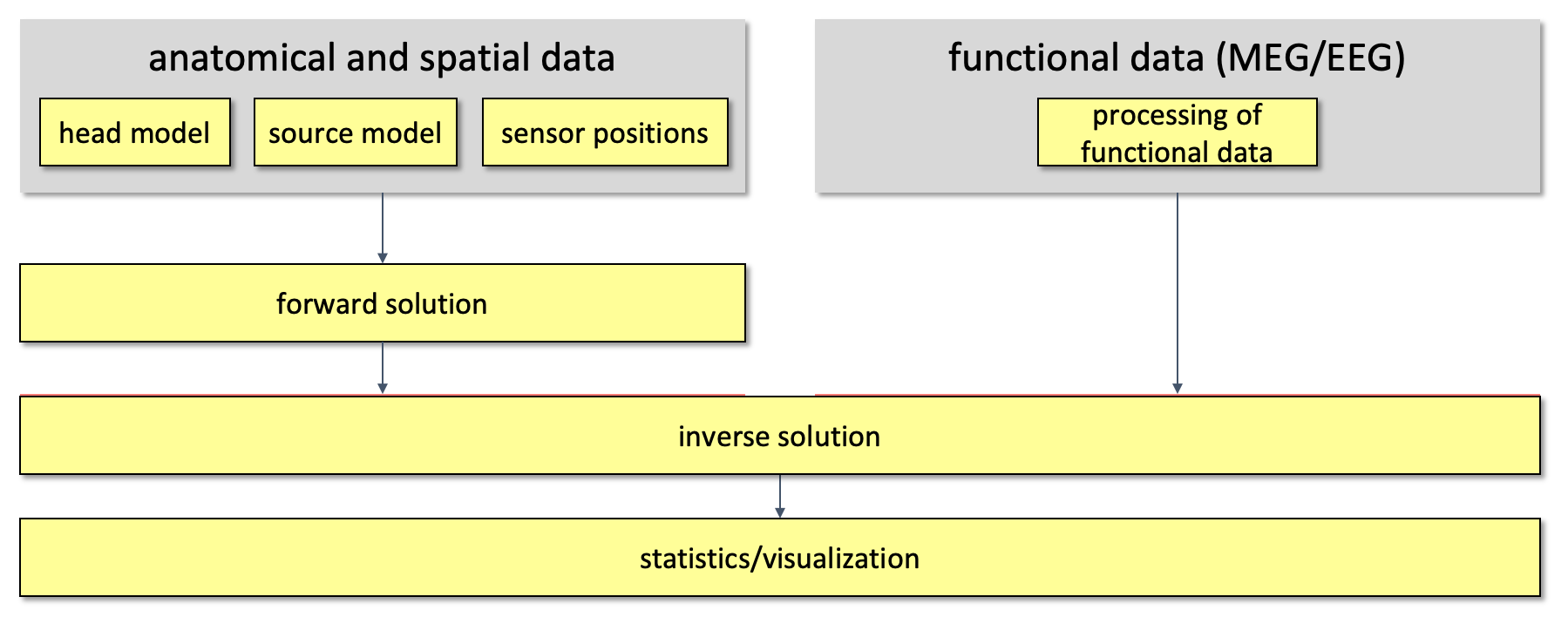
Using this information, source estimation comprises two major steps: (1) Estimation of the EEG potential or MEG field distribution for a known source is referred to as forward modeling. (2) Estimation of the unknown sources corresponding to the measured EEG or MEG is referred to as inverse modeling.
The forward solution can be computed when the head model, the sensor positions and a model for the source are given. For distributed source models and for scanning approaches such as beamforming, the source model consists of a discrete description of the the brain volume or of the cortical sheet in many voxels or vertices. When the forward solution is computed, the lead field matrix (with dimensions Nchan * Nsources) is calculated for each point, taking into account the head model and the sensor positions.
A prerequisite of forward modeling is that the geometrical description of the sensor positions, head model and source model are expressed in the same coordinate system (e.g., CTF, MNI, Talairach) and with the same units (mm, cm, or m). There are different conventions for coordinate systems. The precise coordinate system is not relevant, as long as all data is consistent. Here you can read how the different head and MRI coordinate systems are defined. For most MEG systems, the gradiometers are by default defined relative to head localizer coils or anatomical landmarks, therefore when the anatomical MRI are aligned to the same landmarks, the position of the MEG sensors directly matches the MRI. As EEG data is typically not explicitly aligned relatively to the head, therefore, the EEG electrodes usually have to be explicitly realigned prior to source reconstruction (see also this faq and this example).
Figure 1. Overall outline of the pipeline used for source reconstruction
Procedure
As already mentioned, the goal of this session is to solve the EEG and MEG forward problem, more precisely we want to compute EEG and MEG leadfields so that the inverse problem can be solved in the next session (inverse problem).
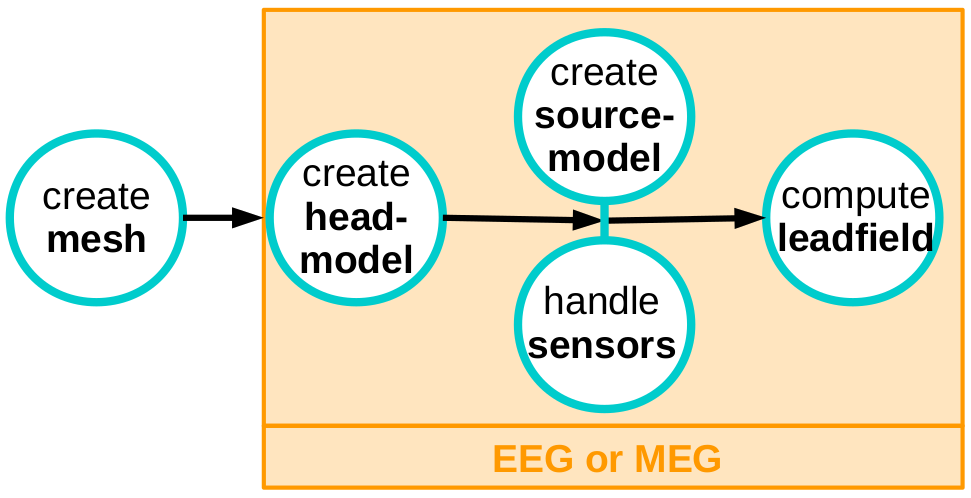
To compute the leadfields, there are five main steps that have to be followed.
- create the mesh: in this step the MRI is loaded and processed, the segmentation is performed and finally the mesh is generated;
- create the headmodel: in this step the geometrical (mesh) and electrical (tissue conductivities) features are merged together;
- create the sourcemodel: in this step a grid of source positions in the gray matter is created;
- handle the sensors: loading the electrodes and the gradiometers and aligning the electrodes to the scalp surface if needed;
- compute the leadfield, i.e., solve the forward problem: this steps consists of two procedures. First, the so-called transfer matrix is computed; second, the leadfield matrix is estimated.
The first step is the same for solving both the EEG and MEG forward problem, the other four have to be executed separately for EEG and MEG. See Figure1.
Figure: pipeline for forward computation using FEM, in the orange box there are the steps which differ between EEG and MEG
In particular, the EEG forward solution is computed via the method so-called simbio which relies on the code that you can find here, while the MEG forward solution calls the duneuro method, which makes use of the code developed in the University of Münster, visit this for further details.
The integration of SimBio with FieldTrip is described in the reference below. Please cite this reference if you use the FieldTrip-SimBio pipeline in your research.
Vorwerk, J., Oostenveld, R., Piastra, M.C., Magyari, L., & Wolters, C. H. The FieldTrip‐SimBio pipeline for EEG forward solutions. BioMed Eng OnLine (2018) 17:37. DOI: 10.1186/s12938-018-0463-y.
1. Create the mesh
This procedure consists in six steps. The input is a T1 weighted MRI and the output is a volumetric mesh with five compartments, i.e., scalp, skull, cerebrospinal fluid (CSF), gray and white matter.
a. load the MRI
mri_orig = ft_read_mri('subject01.nii');
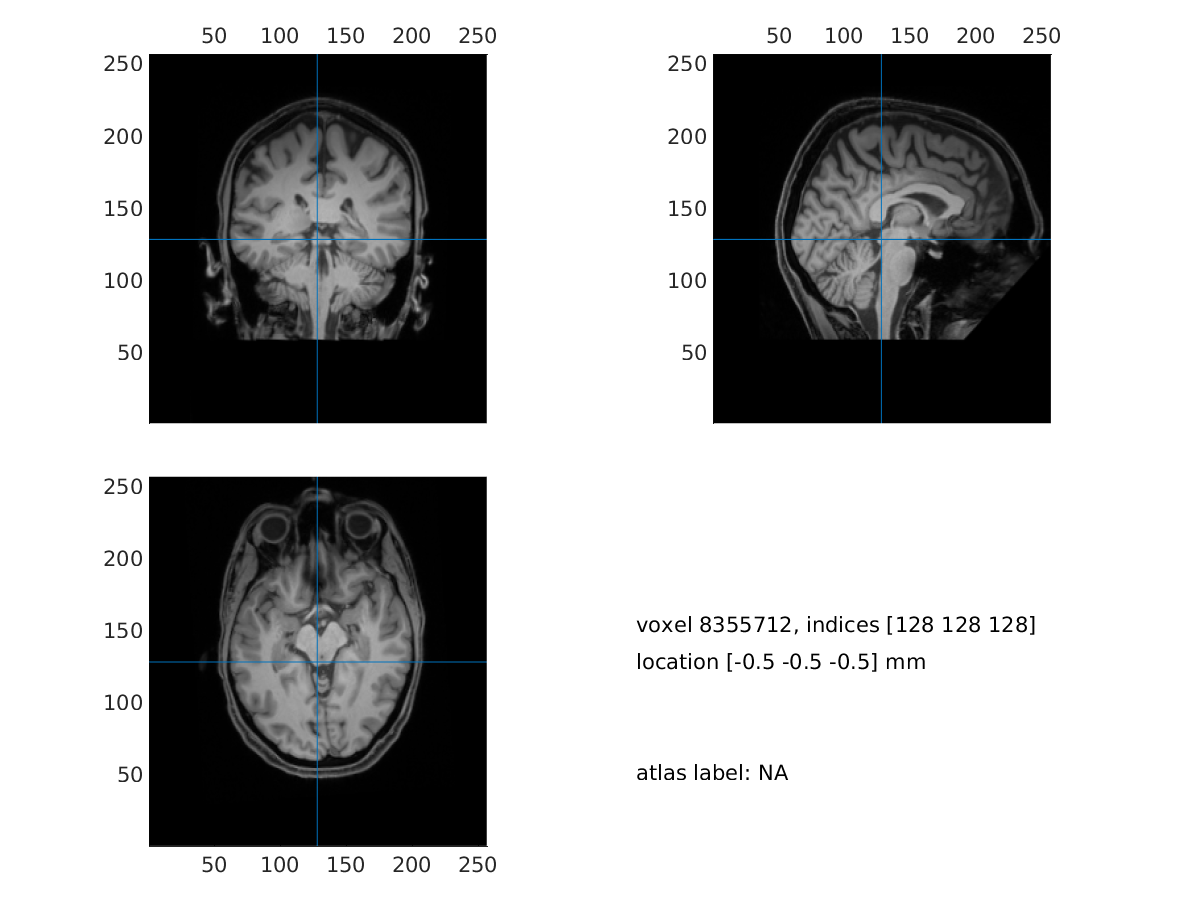
Visualize the MRI
cfg = [];
ft_sourceplot(cfg,mri_orig);
Figure: visualization of the MRI
b. realign the MRI
In this step we will interactively align the MRI to the CTF space. We will be asked to identify the three CTF landmarks (nasion, NAS; right pre-auricular point, RPA; left pre-auricular point, LPA) in the MRI.
cfg = [];
cfg.method = 'interactive';
cfg.coordsys = 'ctf';
mri_realigned = ft_volumerealign(cfg, mri_orig);
We can visualize the realigned MRI
cfg = [];
ft_sourceplot(cfg, mri_realigned);
c. reslice the MRI
cfg = [];
mri_resliced = ft_volumereslice(cfg, mri_realigned);
We can visualize the resliced MRI
cfg = [];
ft_sourceplot(cfg, mri_resliced);
Figure: visualization of the replaced MRI
d. create surface meshes
For visualization purposes, we produce surface meshes for three compartments: scalp, skull and brain. In order to do that, we first have to segment the MRI into the three compartments.
cfg = [];
cfg.output = {'scalp', 'skull', 'brain'};
mri_segmented_3_compartment = ft_volumesegment(cfg, mri_resliced);
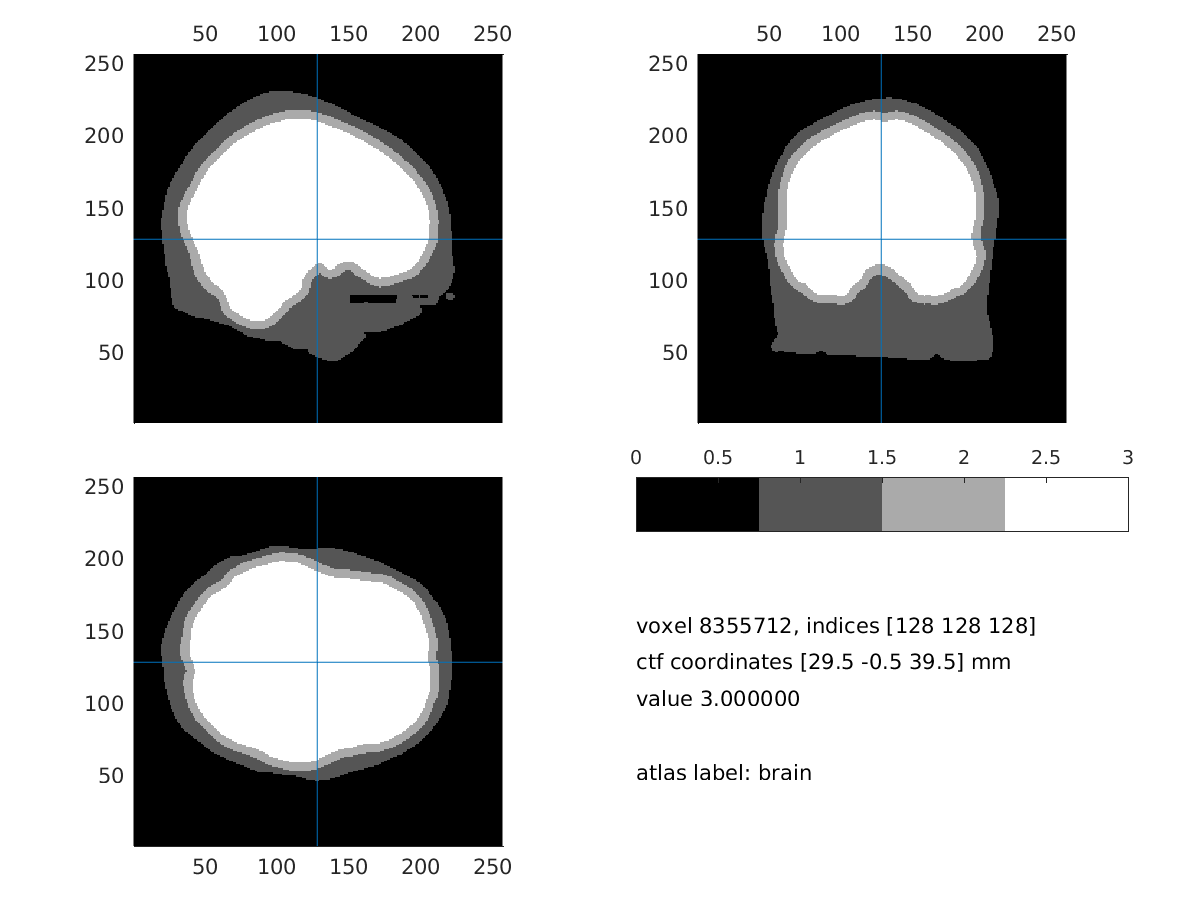
Visualize the segmentation
seg_i = ft_datatype_segmentation(mri_segmented_3_compartment, 'segmentationstyle', 'indexed');
cfg = [];
cfg.funparameter = 'seg';
cfg.funcolormap = gray(4); % distinct color per tissue
cfg.location = 'center';
cfg.atlas = seg_i;
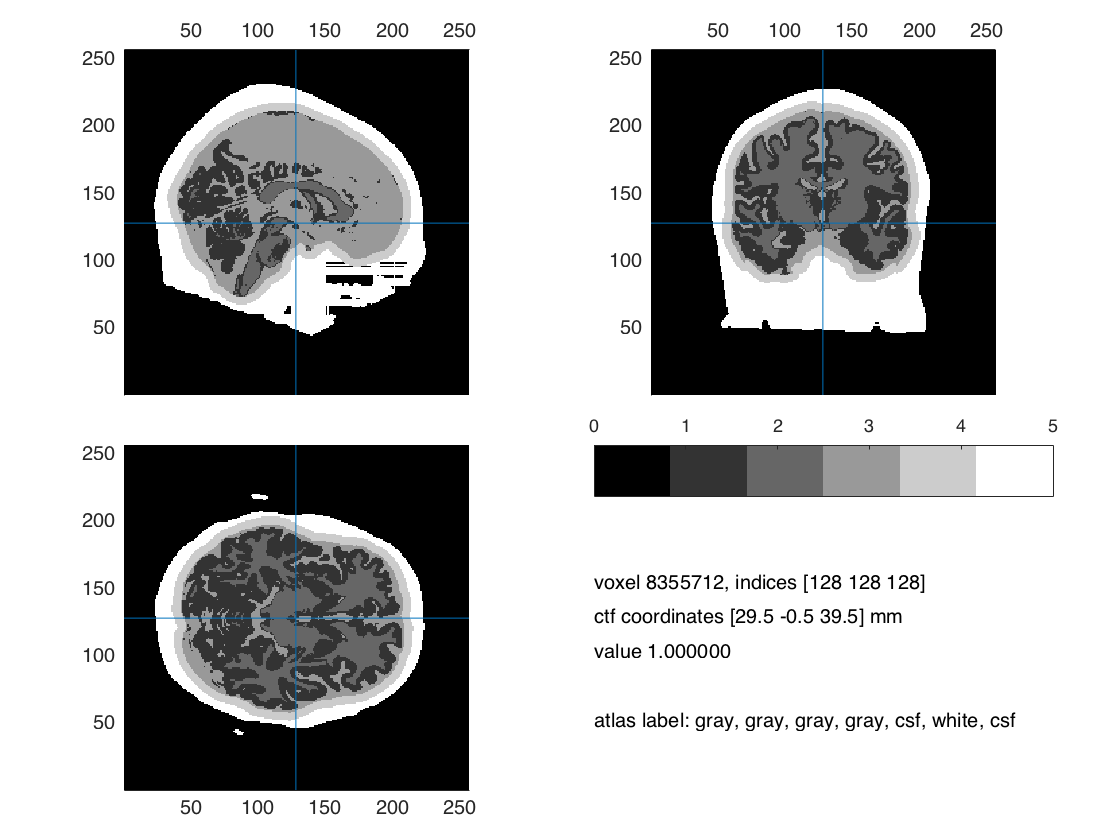
ft_sourceplot(cfg, seg_i);
Figure: three compartment segmentation output
Once the segmentation is completed, the three surface meshes can be computed.
cfg =[];
cfg.tissue = {'scalp', 'skull', 'brain'};
cfg.numvertices = [3000 2000 1000];
mesh_surf = ft_prepare_mesh(cfg,mri_segmented_3_compartment);
We can save the mesh obtained
save mesh_surf mesh_surf
e. segment the MRI
cfg = [];
cfg.output = {'scalp', 'skull', 'csf', 'gray', 'white'};
cfg.brainsmooth = 2;
cfg.skullsmooth = 2;
cfg.scalpsmooth = 2;
mri_segmented_5_compartment = ft_volumesegment(cfg, mri_resliced);
Visualize the segmentation result
seg_i = ft_datatype_segmentation(mri_segmented_5_compartment, 'segmentationstyle', 'indexed');
seg_i = ft_datatype_segmentation(mri_segmented_5_compartment, 'segmentationstyle', 'indexed');
cfg = [];
cfg.funparameter = 'seg';
cfg.funcolormap = gray(6); % distinct color per tissue (air is included)
cfg.location = 'center';
cfg.atlas = seg_i; % the segmentation can also be used as atlas
ft_sourceplot(cfg, seg_i);
Figure: 5 compartment segmentation output.
f. create the mesh
cfg = [];
cfg.shift = 0.3;
cfg.method = 'hexahedral';
cfg.resolution = 2; % this is in mm
cfg.tissue = {'scalp', 'skull', 'csf', 'gray', 'white'};
mesh_fem = ft_prepare_mesh(cfg,mri_segmented_5_compartment);
For this tutorial we downsample the mesh to 2mm resolution, in order to reduce the computation time of the following steps.
EEG and MEG forward solution computation
Once the volumetric mesh has been created, the forward solution can be computed. In the following, steps 2-5 are described for EEG and MEG separately.
Currently, the pipeline for computing the MEG forward problem solution has been tested on Ubuntu systems, where MATLAB should be started with the following command:
BLAS_VERSION=/usr/lib/libblas.so
LD_PRELOAD=/usr/lib/x86_64-linux-gnu/libstdc++.so.6
./matlab
2(EEG). Create the headmodel
cfg = [];
cfg.method = 'simbio';
cfg.conductivity = [0.43 0.01 1.79 0.33 14];
cfg.tissuelabel = {'scalp', 'skull', 'csf', 'gray', 'white'};
headmodel_fem_eeg = ft_prepare_headmodel(cfg, mesh_fem);
Visualize the headmodel and the electrodes (it might take time and memory)
% scalp: 1, skull: 2, csf: 3, gray: 4, wm: 5
ts = 1;
figure
mesh2 =[];
mesh2.hex = headmodel_fem_eeg.hex(headmodel_fem_eeg.tissue==ts,:); %mesh2.hex(1:size(mesh2.hex),:);
mesh2.pos = headmodel_fem_eeg.pos;
mesh2.tissue = headmodel_fem_eeg.tissue(headmodel_fem_eeg.tissue==ts,:); %mesh.tissue(1:size(mesh2.hex),:);
mesh_ed = mesh2edge(mesh2);
patch('Faces',mesh_ed.poly,...
'Vertices',mesh_ed.pos,...
'FaceAlpha',.5,...
'LineStyle', 'none',...
'FaceColor',[1 1 1],...
'FaceLighting', 'gouraud');
xlabel('coronal');
ylabel('sagital');
zlabel('axial')
camlight;
axis on;
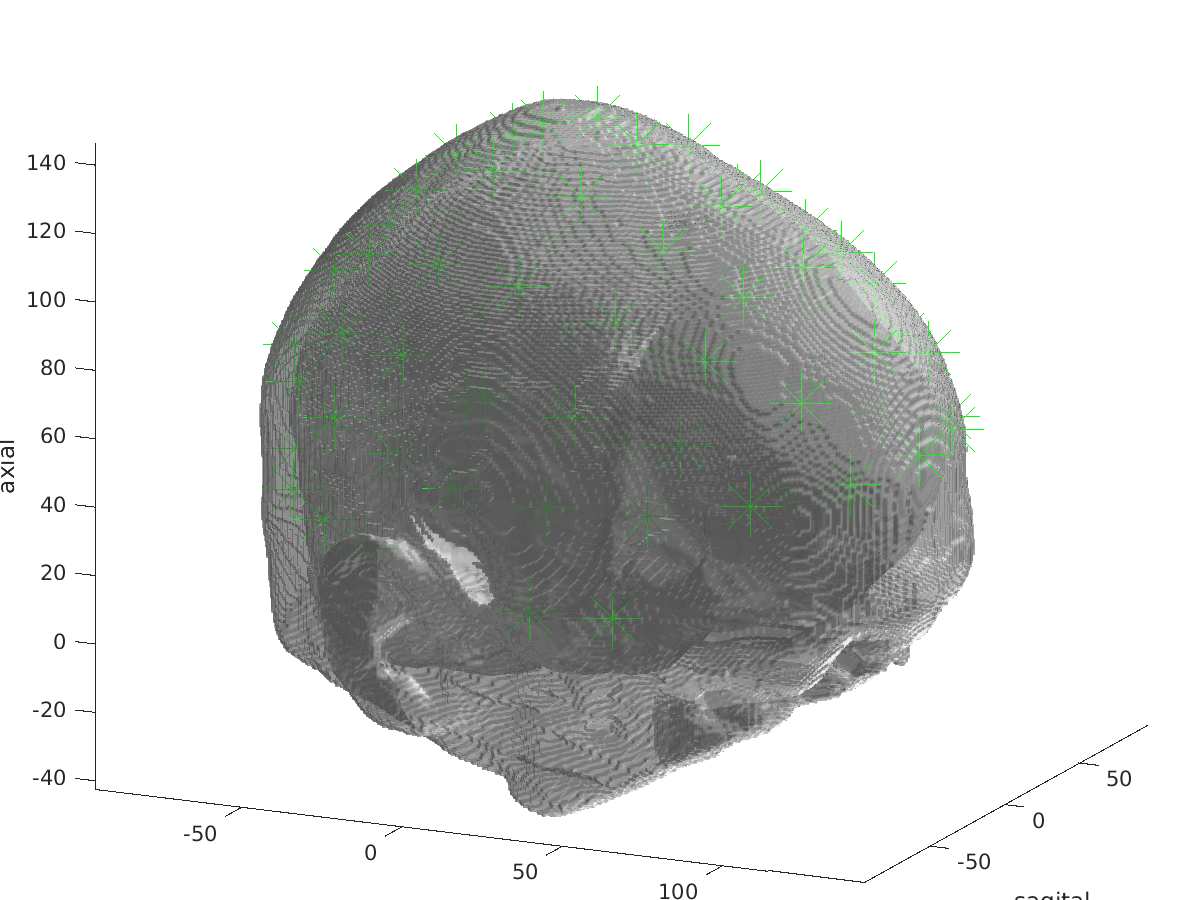
ft_plot_sens(elec, 'style', '*g');
Figure: visualization of headmodel_fem_eeg and electrodes
3(EEG). Create the sourcemodel
In this phase, source locations are selected within the gray matter compartment. During this tutorial we recommend to create a rather coarse grid (cfg.resolution = 5;), in order to be able to compute the forward solution in the time available in this course.
cfg = [];
cfg.resolution = 5; %in mm
cfg.headmodel = headmodel_fem_eeg;
cfg.inwardshift = 1; %shifts dipoles away from surfaces
sourcemodel = ft_prepare_sourcemodel(cfg, headmodel_fem_eeg);
We can visualize the sources and the scalp surface mes
figure, ft_plot_mesh(sourcemodel.pos(sourcemodel.inside,:))
hold on, ft_plot_mesh(mesh_surf(1), 'surfaceonly', 'yes', 'vertexcolor', 'none', 'facecolor',...
'skin', 'facealpha',0.5, 'edgealpha',0.1)
Figure: visualization of the source model
4(EEG). Handle the sensors
In case the electrodes are not aligned to the MRI (i.e., CTF space), we can use the interactive function as follows
cfg = [];
cfg.method = 'interactive';
cfg.elec = elec;
cfg.headshape = mesh_surf(1);
elec = ft_electroderealign(cfg);
Figure: visualization of headmodel_fem_eeg and electrodes
5(EEG). Compute the leadfield
Please DO NOT run ft_prepare_vol_sens in this tutorial session! It will take too much time and memory. Load “headmodel_fem_eeg_tr”.
%% compute the transfer matrix
[headmodel_fem_eeg_tr, elec] = ft_prepare_vol_sens(headmodel_fem_eeg, elec);
%% compute the leadfield
cfg = [];
cfg.grid = sourcemodel;
cfg.headmodel = headmodel_fem_eeg_tr;
cfg.elec = elec;
cfg.reducerank = 3;
leadfield_fem_eeg = ft_prepare_leadfield(cfg);
2(MEG). Create the headmodel
cfg = [];
cfg.method = 'duneuro';
cfg.conductivity = [0.43 0.01 1.79 0.33 0.14]; % check that the order is the same as the one i the mesh_fem
headmodel_fem_meg = ft_prepare_headmodel(cfg, mesh_fem);
3(MEG). Create the sourcemodel
If the sourcemodel was already created at the step 3(EEG), it can be simply loaded for this step.
cfg = [];
cfg.resolution = 5; %in mm
cfg.headmodel = headmodel_fem_meg;
cfg.inwardshift = 1; %shifts dipoles away from surfaces
sourcemodel = ft_prepare_sourcemodel(cfg, headmodel_fem_meg);
We can visualize the sources and the scalp surface mes
figure, ft_plot_mesh(sourcemodel.pos(sourcemodel.inside,:))
hold on, ft_plot_mesh(mesh_surf(1), 'surfaceonly', 'yes', 'vertexcolor', 'none', 'facecolor',...
'skin', 'facealpha',0.5, 'edgealpha',0.1)
4(MEG). Handle the sensors
As already mentioned, the MRI was realigned to the CTF space, therefore there is no need to realign the sensors. We load them from the data.
hdr = ft_read_header('subject01.ds', 'headerformat', 'ctf_ds');
grad_cm = hdr.grad;
grad = ft_convert_units(grad_cm, 'mm');
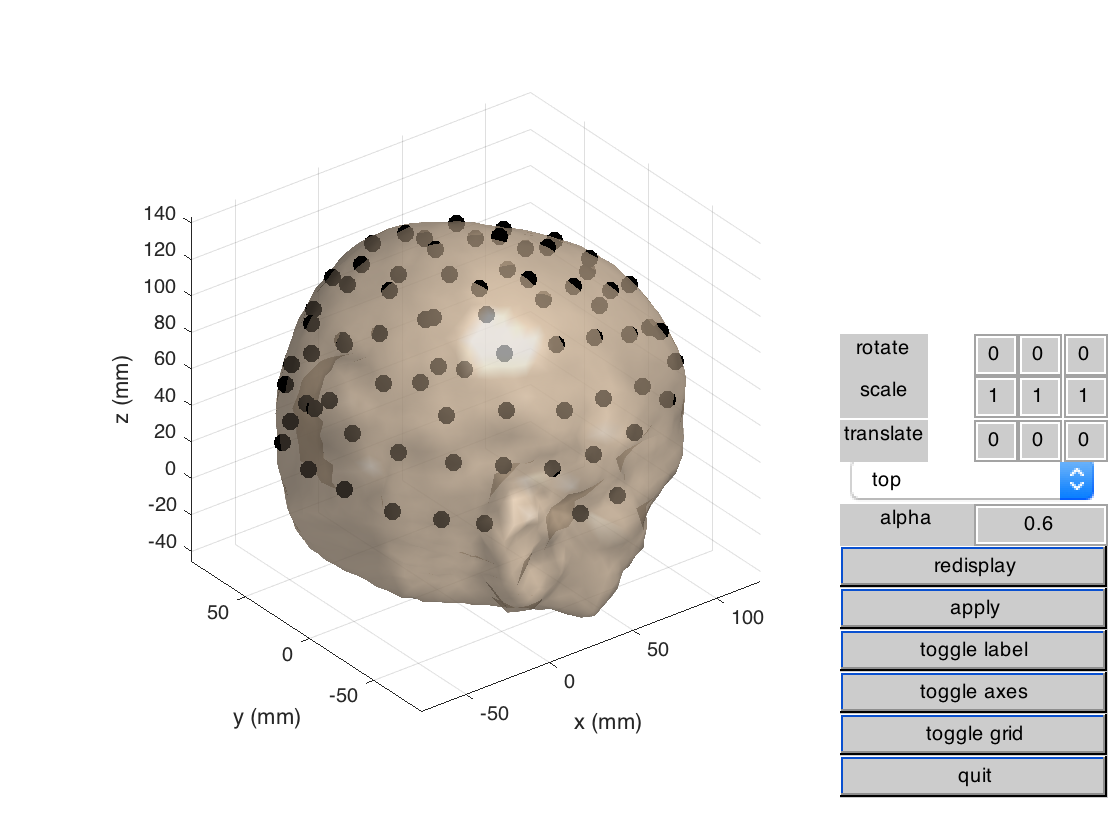
We can visualize both EEG and MEG sensors, together with the scalp surface mesh
figure
hold on
ft_plot_mesh(mesh_fem, 'surfaceonly', 'yes', 'vertexcolor', 'none', 'edgecolor', 'none', 'facecolor',[0.5 0.5 0.5], 'facealpha',0.1, 'edgealpha', 0.1);
camlight
axis on
ft_plot_sens(grad, 'style', 'sr', 'coil', 'yes');
ft_plot_sens(elec);
5(MEG). Compute the leadfield
Please DO NOT run ft_prepare_vol_sens in this tutorial session! It will take too much time and memory. Load the file headmodel_fem_eeg_tr.mat from disk.
%% compute the transfer matrix
[headmodel_fem_meg_tr, grad] = ft_prepare_vol_sens(headmodel_fem_meg, grad, 'channel', MEG_avg.label);
load headmodel_fem_meg_tr
meg_transfer = headmodel_fem_meg_tr.meg_transfer;
headmodel_fem_meg_tr =headmodel_fem_meg;
headmodel_fem_meg_tr.meg_transfer = meg_transfer;
%% compute the leadfield
cfg = [];
cfg.grid = sourcemodel;
cfg.headmodel = headmodel_fem_meg_tr;
cfg.grad = grad;
cfg.reducerank = 2;
leadfield_fem_meg = ft_prepare_leadfield(cfg);
Exercises
Exercise 1
Realign the electrodes in the file elec_shifted.mat to the headmodel you created.
Exercise 2
Compute a finer sourcemodel, e.g., 2 mm resolution and compute the respective EEG and MEG forward solutions.
Exercise 3
Compute the EEG and MEG forward solution using the Boundary Element Method (BEM), e.g., following this tutorial.
Summary and Comments
This tutorial was about the computation of leadfields that could be feed into the inverse problem which will be explain in the part on the inverse problem.
This tutorial was last tested on 14-06-2018 by Simon Homölle on Mac, Matlab 2015b.