Event-related averaging and MEG planar gradient

Introduction

This tutorial works on the MEG-language dataset, you can click here for details on the dataset. This tutorial is a continuation from the preprocessing tutorials. We will begin by repeating some code used to select the trials and preprocess the data as described in the earlier tutorials (trigger-based trial selection, visual artifact rejection).

In this tutorial you will learn how to compute an event-related potential (ERP) or event-related field (ERF) and how to calculate the planar gradient (in case the MEG data was acquired by axial-gradiometer sensors). You will also learn how to visualize the results of the ERP/ERF analysis, and how to average the results across subjects.

This tutorial assumes that the steps of preprocessing are already clear for the reader. This tutorial does not show how to do statistical analysis on the ERF/ERPs. You can find more information about the statistics in the Parametric and non-parametric statistics on event-related fields tutorial. If you are interested in the event-related changes in the oscillatory components of the EEG/MEG signal, you can check out the Time-frequency analysis using Hanning window, multitapers and wavelets tutorial.

Background

ERP / ERF

When analyzing EEG or MEG signals, the aim is to investigate the modulation of the measured brain signals with respect to a certain event. However, due to intrinsic and extrinsic noise in the signals - which in single trials is often higher than the signal evoked by the brain - it is typically required to average data from several trials to increase the signal-to-noise ratio(SNR). One approach is to repeat a given event in your experiment and average the corresponding EEG/MEG signals. The assumption is that the noise is independent of the events and thus reduced when averaging, while the effect of interest is time-locked to the event. The approach results in ERPs and ERFs for respectively EEG and MEG. Timelock analysis can be used to calculate ERPs/ ERFs.

Planar gradient

The CTF MEG system has (151 in this dataset, or 275 in newer systems) first-order axial gradiometer sensors that measure the gradient of the magnetic field in the radial direction, i.e. orthogonal to the scalp. Often it is helpful to interpret the MEG fields after transforming the data to a planar gradient configuration, i.e. by computing the gradient tangential to the scalp. This representation of MEG data is comparable to the field measured by planar gradiometer sensors. One advantage of the planar gradient transformation is that the signal amplitude typically is largest directly above a source.

The dataset used for this tutorial

The dataset that we use in this (and many other) tutorial(s), is the Subject01.ds dataset. This is data obtained with a 151-channel CTF MEG system, while the participant listened to Dutch sentences. The experimental manipulation was designed to investigate the brain effects of semantic (in)congruency.

Procedure

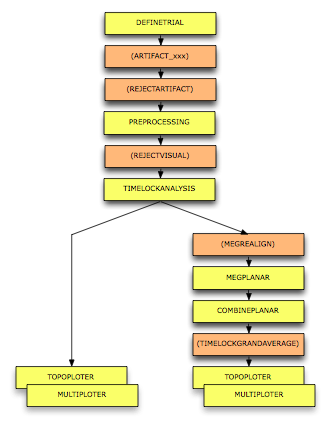
To calculate the event-related field / potential for the example dataset we will perform the following steps:

• Read the data into MATLAB using ft_definetrial and ft_preprocessing
• Seperate the trials from each condition using ft_selectdata
• Compute the average over trials using the function ft_timelockanalysis
• Calculate the planar gradient with the functions ft_megplanar and ft_combineplanar
• Visualize the results. You can plot the ERF/ ERP of one channel with ft_singleplotER or several channels with ft_multiplotER, or by creating a topographic plot for a specified time- interval with ft_topoplotER
• Grandaverage and realignment (optional). When you have data from more than one subject you can make a grand average of the ERPs / ERFs with ft_timelockgrandaverage.

Figure: A schematic overview of the steps in averaging of event-related fields.

Preprocessing

Reading in the data

We will now read and preprocess the data. If you would like to continue directly with the already preprocessed data, you can download dataFIC_LP.mat, dataFC_LP.mat and dataIC_LP.mat. Load the data into MATLAB with the command load and skip to Timelockanalysis.

Otherwise run the following code:

The ft_definetrial and ft_preprocessing functions require the original MEG dataset, which is available here

Do the trial definition for the all conditions together:

cfg                         = [];
cfg.dataset                 = 'Subject01.ds';
cfg.trialfun                = 'ft_trialfun_general'; % this is the default
cfg.trialdef.eventtype      = 'backpanel trigger';
cfg.trialdef.eventvalue     = [3 5 9]; % the values of the stimulus trigger for the three conditions
% 3 = fully incongruent (FIC), 5 = initially congruent (IC), 9 = fully congruent (FC)
cfg.trialdef.prestim        = 1; % in seconds
cfg.trialdef.poststim       = 2; % in seconds

cfg = ft_definetrial(cfg);

Cleaning

% remove the trials that have artifacts from the trl
cfg.trl([2, 5, 6, 8, 9, 10, 12, 39, 43, 46, 49, 52, 58, 84, 102, 107, 114, 115, 116, 119, 121, 123, 126, 127, 128, 133, 137, 143, 144, 147, 149, 158, 181, 229, 230, 233, 241, 243, 245, 250, 254, 260],:) = [];

% preprocess the data
cfg.channel    = {'MEG', '-MLP31', '-MLO12'};        % read all MEG channels except MLP31 and MLO12
cfg.demean     = 'yes';
cfg.baselinewindow  = [-0.2 0];
cfg.lpfilter   = 'yes';                              % apply lowpass filter
cfg.lpfreq     = 35;                                 % lowpass at 35 Hz.

data_all = ft_preprocessing(cfg);

These data have been cleaned from artifacts by removing several trials and two sensors; see the visual artifact rejection tutorial.

For subsequent analysis we split the data into three different data structures, one for each condition (fully incongruent condition FIC, fully congruent condition FC, and initially congruent IC).

cfg = [];
cfg.trials = data_all.trialinfo == 3;
dataFIC_LP = ft_selectdata(cfg, data_all);

cfg = [];
cfg.trials = data_all.trialinfo == 5;
dataIC_LP = ft_selectdata(cfg, data_all);

cfg = [];
cfg.trials = data_all.trialinfo == 9;
dataFC_LP = ft_selectdata(cfg, data_all);

Subsequently you can save the data to disk.

  save dataFIC_LP dataFIC_LP
  save dataFC_LP dataFC_LP
  save dataIC_LP dataIC_LP

If preprocessing was done as described, the data structure will have the following fields:

dataFIC_LP =
         hdr: [1x1 struct]
       label: {149x1 cell}
        time: {1x77 cell}
       trial: {1x77 cell}
     fsample: 300
  sampleinfo: [77x2 double]
   trialinfo: [77x1 double]
        grad: [1x1 struct]
        elec: [1x1 struct]
         cfg: [1x1 struct]

Note that ‘dataFIC_LP.label’ has 149 in stead of 151 labels since channels MLP31 and MLO12 were excluded. ‘dataFIC-LP.trial’ has 76 in stead of 87 trials because 10 trials were rejected because of artifacts.

The most important fields are ‘dataFIC_LP.trial’ containing the individual trials and ‘data.time’ containing the time vector for each trial. To visualize the single trial data (trial 1) of a single channel (channel 130) you can do the following:

plot(dataFIC_LP.time{1}, dataFIC_LP.trial{1}(130,:))

Figure: The MEG data from a single trial in a single sensor obtained after ft_preprocessing.

Timelockanalysis

The function ft_timelockanalysis makes averages of all the trials in a data structure. It requires preprocessed data (see above), which is available from dataFIC_LP.mat, dataFC_LP.mat and dataIC_LP.mat.

load dataFIC_LP
load dataFC_LP
load dataIC_LP

The trials belonging to one condition will now be averaged with the onset of the stimulus time aligned to the zero-time point (the onset of the last word in the sentence). This is done with the function ft_timelockanalysis. The input to this procedure is the dataFIC_LP structure generated by ft_preprocessing. No special settings are necessary here. Thus specify an empty configuration.

cfg = [];
avgFIC = ft_timelockanalysis(cfg, dataFIC_LP);
avgFC = ft_timelockanalysis(cfg, dataFC_LP);
avgIC = ft_timelockanalysis(cfg, dataIC_LP);

The output is the data structure avgFIC with the following fields:

avgFIC =
      time: [-1 -0.9967 -0.9933 -0.9900 -0.9867 … ]
     label: {149x1 cell}
      elec: [1x1 struct]
      grad: [1x1 struct]
       avg: [149x900 double]
       var: [149x900 double]
       dof: [149x900 double]
    dimord: 'chan_time'
       cfg: [1x1 struct]

The most important field is avgFIC.avg, containing the average over all trials for each sensor.

Plot the results (axial gradients)

Using the plot functions ft_multiplotER, ft_singleplotER and ft_topoplotER you can make plots of the average. You can find information about plotting also in the Plotting data at the channel and source level tutorial.

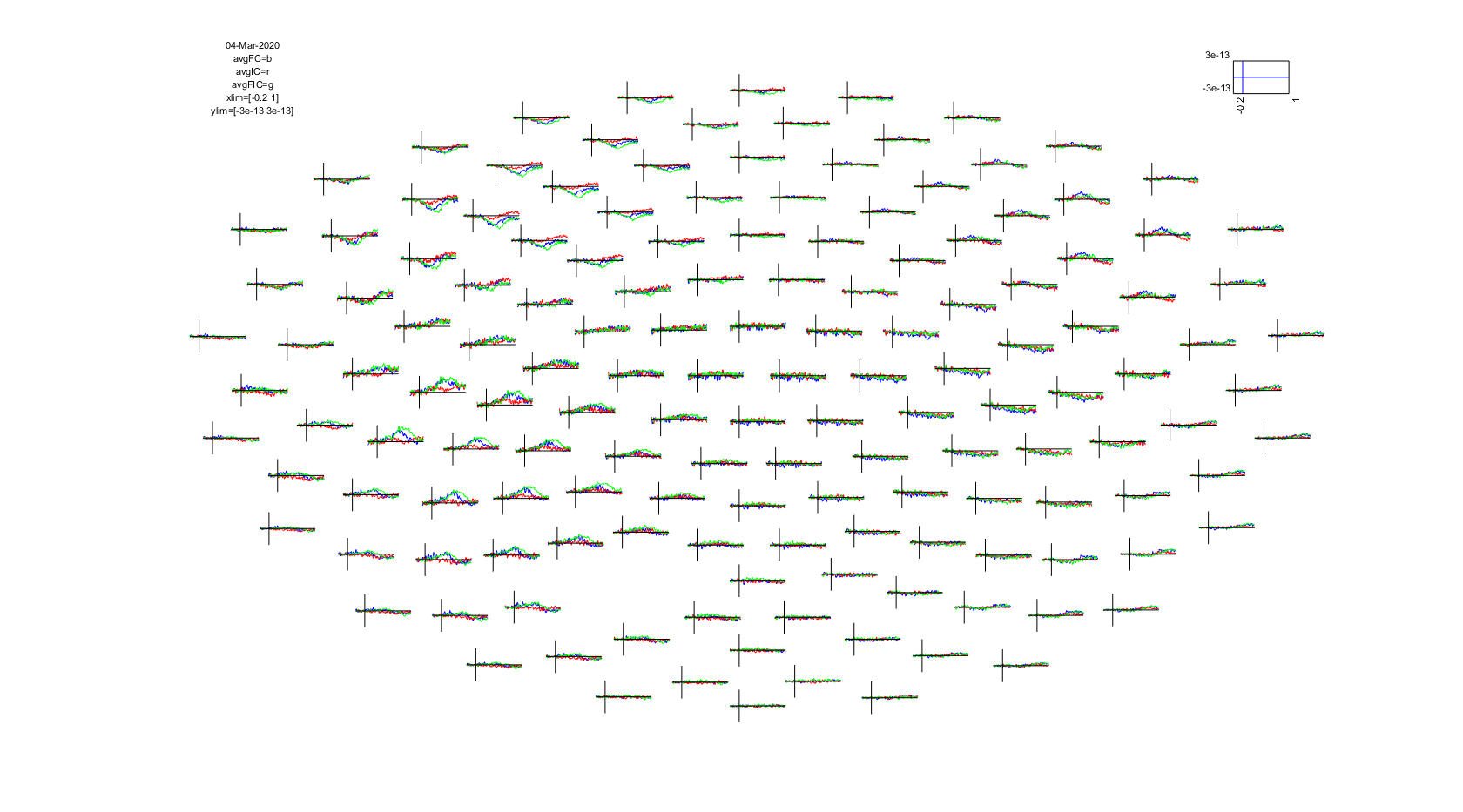
Use ft_multiplotER to plot all sensors in one figure:

cfg = [];
cfg.showlabels = 'yes';
cfg.fontsize = 6;
cfg.layout = 'CTF151_helmet.mat';
cfg.ylim = [-3e-13 3e-13];
ft_multiplotER(cfg, avgFIC);

Figure: The event-related fields plotted using ft_multiplotER. The event-related fields were calculated using ft_preprocessing followed by ft_timelockanalysis.

This plots the event-related fields for all sensors arranged topographically according to their position in the helmet. You can use the zoom button (magnifying glass) to enlarge parts of the figure. You can use multiple data arguments in the input, and these will be displayed together:

cfg = [];
cfg.showlabels = 'no';
cfg.fontsize = 6;
cfg.layout = 'CTF151_helmet.mat';
cfg.baseline = [-0.2 0];
cfg.xlim = [-0.2 1.0];
cfg.ylim = [-3e-13 3e-13];
ft_multiplotER(cfg, avgFC, avgIC, avgFIC);

Figure: The event-related fields for three conditions plotted simultaneously using ft_multiplotER.

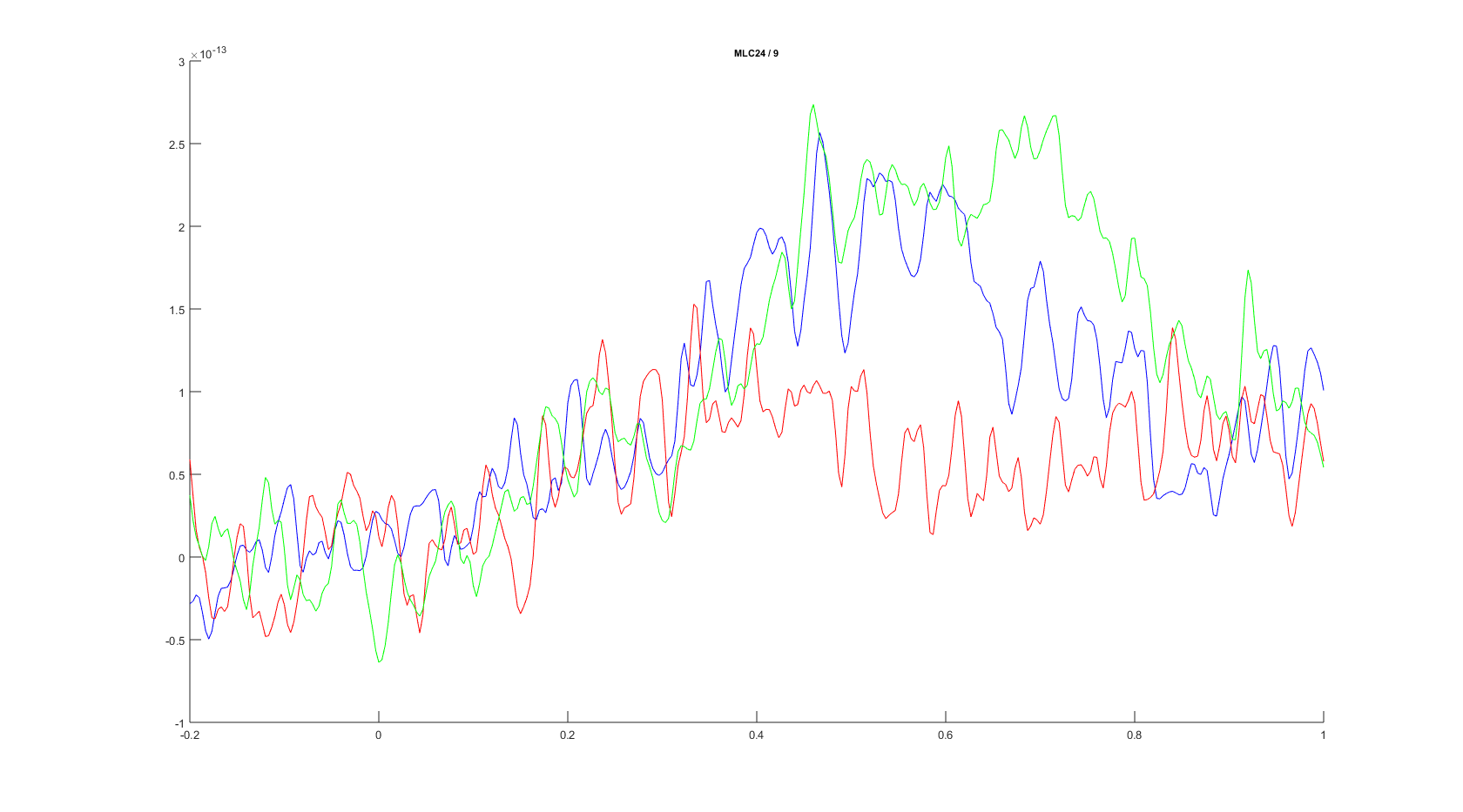
To plot the data of a single sensor you can use ft_singleplotER while specifying the name of the channel you are interested in, for instance MLC24:

cfg = [];
cfg.xlim = [-0.2 1.0];
cfg.ylim = [-1e-13 3e-13];
cfg.channel = 'MLC24';
ft_singleplotER(cfg, avgFC, avgIC, avgFIC);

Figure: The event-related fields plotted for three conditions for sensor MLC24 using ft_singleplotER.

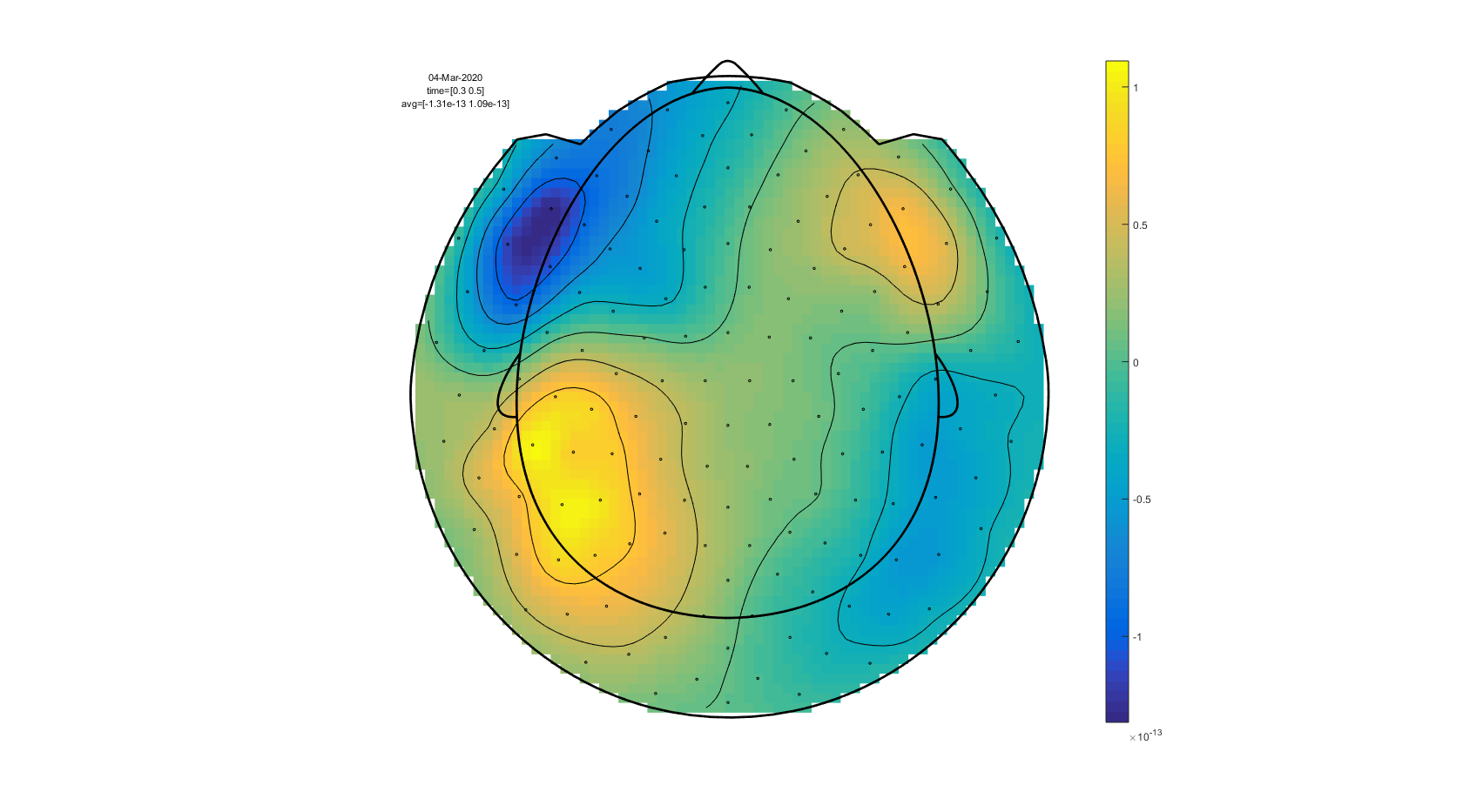
To plot the topographic distribution of the data averaged over the time interval from 0.3 to 0.5 seconds you can use the following command:

cfg = [];
cfg.xlim = [0.3 0.5];
cfg.colorbar = 'yes';
cfg.layout = 'CTF151_helmet.mat';
ft_topoplotER(cfg, avgFIC);

Figure: A topographic plot of the event-related fields obtained using ft_topoplotER.

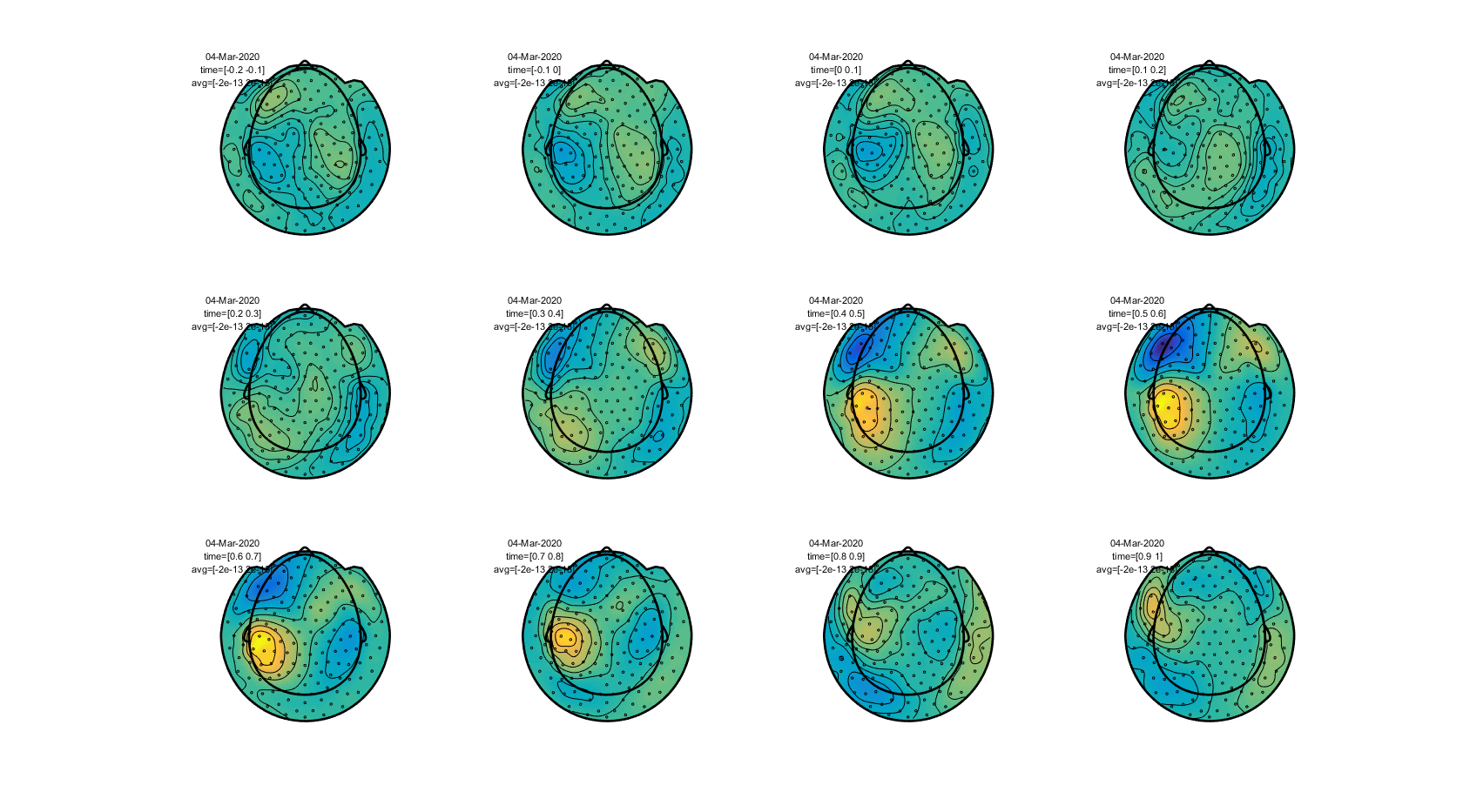
To plot a sequence of topographic plots you can define cfg.xlim to be a vector:

cfg        = [];
cfg.xlim   = [-0.2 : 0.1 : 1.0];  % Define 12 time intervals
cfg.zlim   = [-2e-13 2e-13];      % Set the 'color' limits.
cfg.layout = 'CTF151_helmet.mat';
ft_topoplotER(cfg, avgFIC);

Figure: The topography of event-related fields over time obtained using ft_topoplotER.

Exercise 1

Exercise 2

Calculate the planar gradient

With ft_megplanar we calculate the planar gradient of the averaged data. Ft_megplanar is used to compute the gradient of the magnetic field that is tangential to the head surface. This leads to a 2-dimensional signal at each of the sensor locations, which are denoted as ‘horizontal’ and ‘vertical’ components of the planar gradient. This terminology is based on the analogy with a 2-dimensional Cartesian coordinate system, with a horizontal and vertical axis: the gradient axes are not ‘horizontal’ and ‘vertical’ w.r.t. the surroundings.

The planar gradient at a given sensor location can be approximated by comparing the field at that sensor with its neighbors (i.e. by means of a finite difference estimate of the derivative). To compute the magnitude of the gradient, the two orthogonal gradients on a single sensor location can be combined using Pythagoras rule with the FieldTrip function ft_combineplanar.

Calculate the planar gradient of the averaged data:

cfg                 = [];
cfg.feedback        = 'yes';
cfg.method          = 'template';
cfg.neighbours      = ft_prepare_neighbours(cfg, avgFIC);

cfg.planarmethod    = 'sincos';
avgFICplanar        = ft_megplanar(cfg, avgFIC);

Compute the magnitude of the planar gradient by combining the horizontal and vertical components of the planar gradient according to Pythagoras rule:

cfg = [];
avgFICplanarComb = ft_combineplanar(cfg, avgFICplanar);

Plot the results (planar gradients)

To compare the axial gradient data to the planar gradient data we plot them both in one figure here.

Plot the results of the field of the axial gradiometers and the planar gradient to compare the topographies:

cfg = [];
cfg.xlim = [0.3 0.5];
cfg.zlim = 'maxmin';
cfg.colorbar = 'yes';
cfg.layout = 'CTF151_helmet.mat';
cfg.figure  = subplot(121);
ft_topoplotER(cfg, avgFIC)

colorbar; % you can also try out cfg.colorbar = 'south'

cfg.zlim = 'maxabs';
cfg.layout = 'CTF151_helmet.mat';
cfg.figure  = subplot(122);
ft_topoplotER(cfg, avgFICplanarComb);

Figure: A comparison of event-related fields from the axial gradiometers (left) and the planar gradient (right). The planar gradient was calculated using ft_megplanar and ft_combineplanar.

Exercise 3

Grand average over subjects

Finally you can make a grand-average over all our four subjects with ft_timelockgrandaverage. Before calculating the grand average, the data of each subject can be realigned to standard sensor positions with ft_megrealign. For this step, there are the additional datasets Subject02.zip, Subject03.zip, and Subject04.zip.

For more information about this, type the following commands in the MATLAB command window.

help ft_timelockgrandaverage
help ft_megrealign

Summary and suggested further reading

This tutorial covered how to do event-related averaging on EEG/MEG data, and on how to plot the results. The tutorial gave also information about how to average the results across subjects. After calculating the ERPs/ERFs for each subject and for each condition in an experiment, it is a relevant next step to see if there are statistically significant differences in the amplitude of the ERPs/ERFs between the conditions. If you are interested in this, you can continue with the event-related statistics tutorial.

If you are interested in a different analysis of your data that shows event-related changes in the oscillatory components of the signal, you can continue with the time-frequency analysis tutorial.

See also

• What kind of filters can I apply to my data?

• Fit a dipole to the tactile ERF after mechanical stimulation