Group-level statistics with parametric and non-parametric methods
This tutorial was written specifically for the PracticalMEEG workshop in Aix-en-Provence in December 2022 and is part of a coherent sequence of tutorials. It is an adjusted version of the event-related statistics tutorial and an updated version of the corresponding tutorial for Paris 2019.
Introduction
This tutorial provides an introduction into different options for statistical analysis. Here we will use event-related fields (ERFs) that are estimated at the source level for a cortical-sheet parcellation. This type of data representation can also be referred to as “virtual channels”, since the source activity is represented in the same way as if there were iEEG electrodes placed in the brain.
To introduce the issue of multiple comparisons, we will start with an analysis for a single hand-picked channel/parcel analysis. After that we will consider analyses that take all virtual channels and all timepoints into account. We will start with some basic statistical testing using the MATLAB statistics toolbox and compare the results with that from using the FieldTrip ft_timelockstatistics function. Topics that will be covered are parametric statistics on a single channel and time-window, the multiple comparison problem (MCP), non-parametric randomization testing and cluster-based testing.
This tutorial uses the same multimodal faces as the other tutorials in this series. However, here we will deal with (statistical) analyses on the group level. We will look at differences between the familiar, unfamiliar and scrambled face conditions in a within-subjects design. The processed dataset in this tutorial contains source reconstructed data from all 20 subjects. The virtual-channel ERFs were obtained using ft_sourceanalysis and ft_sourceparcellate. For the purpose of inspecting your data visually, we also use the channel-level plotting functions and ft_timelockgrandaverage to calculate the grand average across participants.
Note that in this tutorial we will not provide detailed information about statistics on channel-level power spectra, time-frequency representations of power (as obtained from ft_freqanalysis), nor on high-density volumetric or cortical sheet source reconstruction results. However, FieldTrip does have similar statistical options for this as well: at the sensor-level we have the ft_freqstatistics function, and on the source-level (statistics on source reconstructed activity), we have the ft_sourcestatistics function.
A more thorough discussion of randomization tests and cluster-based statistics is presented in the Cluster-based permutation tests on event-related fields and the Cluster-based permutation tests on time-frequency data tutorials.
Background
The topic of this tutorial is the statistical analysis of MEG and EEG data. In experiments, the data is usually collected in different experimental conditions, and the experimenter wants to know, by means of statistical testing, whether there is a difference in the data observed in these conditions. Such a comparison between conditions is considered statistically significant if it is unlikely to have occurred by chance according to a predetermined threshold probability, the significance level.
An important feature of the MEG and EEG data is that it has a spatial temporal structure, i.e. the data is sampled at multiple time-points and sensors, or after source reconstruction: multiple locations in the brain. The nature of the data influences which kind of statistics is the most suitable for comparing conditions. If the experimenter is interested in a difference in the signal at a pre-specified time-point and sensor, then the more widely used parametric tests are applicable. If it is not possible to predict a-priori where the differences are, then many statistical comparisons are necessary, which lead to the multiple comparisons problem (MCP). The MCP arises from the fact that the effect of interest (i.e., a difference between experimental conditions) is evaluated at a very large number of (channel,time)-pairs. This number is usually in the order of several thousands. Now, the MCP involves that, due to the large number of comparisons (one per (channel,time)-pair). It is not possible to control the so called family-wise error rate (FWER) by means of the standard statistical procedures that operate at the level of single (channel,time)-pairs. The FWER is the probability, under the hypothesis of no effect, of falsely concluding that there is a difference between the experimental conditions at one or more (channel,time)-pairs. A solution of the MCP requires a procedure that controls the FWER at some critical alpha-level (typically, 0.05 or 0.01). The FWER is also called the false alarm rate.
When parametric statistics are used, one method that addresses this problem is the so-called Bonferroni correction. The idea is if the experimenter is conducting n number of statistical tests then each of the individual tests should be tested under a significance level that is divided by n. The Bonferroni correction was derived from the observation that if n tests are performed with an alpha significance level, then the probability that one comes out significantly is smaller than or equal to n times alpha (Boole’s inequality). In order to keep this probability lower, we can use an alpha that is divided by n for each test. However, the correction comes at the cost of increasing the probability of false negatives, i.e. the test does not have enough power to reveal differences among conditions.
In contrast to the familiar parametric statistical framework, it is straightforward to solve the MCP in the nonparametric framework. Nonparametric tests offer more freedom to the experimenter regarding which test statistics are used for comparing conditions, and help to maximize the sensitivity to the expected effect. For more details see the publication by Maris and Oostenveld (2007) and the Cluster-based permutation tests on event-related fields and the Cluster-based permutation tests on time-frequency data tutorials.
Procedure
To do parametric or non-parametric statistics on virtual-channel event-related fields in a within-subject design, we will use the dataset of 20 subjects that has been preprocessed, source-reconstructed, and averaged over cortical parcels.
We will perform the following steps in this tutorial:
- We will visually inspect the data and look where are differences between the conditions by plotting the grand-averages and subject-averages using the ft_multiplotER, the ft_singleplotER and the MATLAB plot functions. Note that in practice you should not guide your statistical analysis by a visual inspection of the data; you should state your hypothesis up-front and avoid data dredging or p-hacking.
- We will use the standard MATLAB functions for statistical testing in the channel and time of interest
- We will use ft_timelockstatistics for statistical testing in the channel and time of interest
- We will test all channels and latencies and consider multiple comparison corrections
- We will do a non-parametric test with clustering
Reading-in preprocessed and time-locked data in planar gradient format, and grand averaged data
To begin with we will load the source reconstructed and parcellated results from all individual subjects. These result from the source analysis pipeline. The result of the source analysis pipeline is represented in the variable mom, which stands for “dipole moment”. However, the FieldTrip code that we will use in this hands-on session expects channel-level data; hence we will rename the mon variable into avg to make the data appear as if it is the result of a straightforward channel-level analysis.
% load individual subject data
clear subj
iSub = 0;
for k = [1:8 10:16]
iSub = iSub+1;
subj(iSub) = datainfo_subject(k);
end
for k = 1:numel(subj)
filename = fullfile(subj(k).outputpath, 'sourceanalysis', subj(k).name, sprintf('%s_source_parc', subj(k).name));
% load the data from the file, organize each condition in a cell-array
dum = load(filename, 'avg_famous', 'avg_unfamiliar', 'avg_scrambled');
% the parameter of interst is "mom", which we rename here to "avg" for convenience
dum.avg_famous.avg = dum.avg_famous.mom;
dum.avg_famous.dimord = dum.avg_famous.momdimord;
dum.avg_famous = removefields(dum.avg_famous, {'mom', 'momdimord'});
dum.avg_unfamiliar.avg = dum.avg_unfamiliar.mom;
dum.avg_unfamiliar.dimord = dum.avg_unfamiliar.momdimord;
dum.avg_unfamiliar = removefields(dum.avg_unfamiliar, {'mom', 'momdimord'});
dum.avg_scrambled.avg = dum.avg_scrambled.mom;
dum.avg_scrambled.dimord = dum.avg_scrambled.momdimord;
dum.avg_scrambled = removefields(dum.avg_scrambled, {'mom', 'momdimord'});
avg_famous{k} = dum.avg_famous;
avg_unfamiliar{k} = dum.avg_unfamiliar;
avg_scrambled{k} = dum.avg_scrambled;
clear dum
end
On a technical note, it is preferred to represent the multi-subject data as a cell-array of structures, rather than a so-called struct-array. The reason for this is that the cell-array representation allows for easy expansion into a MATLAB function that allows for a variable number of input arguments (which is how the ft_XXXstatistics functions have been designed).
Parametric statistics
A single comparison (t-test)
Plotting the grand-average and the subject-averages
As you might be familiar with, it is always a good idea to visually inspect your data prior to applying any statistical analyses. Below we show a couple ways of plotting data: the grand average across all (subjects) for all sensors and one specific sensor, as well as plotting the individual average for multiple subjects next to each other.
We can calculate the grand-average over subjects for each of the conditions.
% calculate grand average for each condition
cfg = [];
cfg.channel = 'all';
cfg.latency = 'all';
cfg.parameter = 'avg';
grandavg_famous = ft_timelockgrandaverage(cfg, avg_famous{:});
grandavg_unfamiliar = ft_timelockgrandaverage(cfg, avg_unfamiliar{:});
grandavg_scrambled = ft_timelockgrandaverage(cfg, avg_scrambled{:});
% "{:}" means to use data from all elements of the cell-array
Now we plot all channels with ft_multiplotER to find a channel of interest. Since the data represents virtual-channel timeseries, we cannot use a standard (helmet or head-like) layout. Instead we use a regular ordered layout. See also this section in the plotting tutorial. Using the inflated representation of the cortical surface, it would be possible to make a nicer layout, but that is out of scope for this tutorial.
%% virtual channels are not arranged according to a known layout
cfg = [];
cfg.rows = 20;
cfg.columns = 20;
cfg.layout = 'ordered';
layout = ft_prepare_layout(cfg, grandavg_famous);
ft_plot_layout(layout, 'interpreter', 'none', 'fontsize', 8)
Using this layout, we can plot all channels:
cfg = [];
cfg.layout = layout;
ft_multiplotER(cfg, grandavg_famous, grandavg_unfamiliar, grandavg_scrambled);
Figure; ERPs for each virtual channel (parcel)
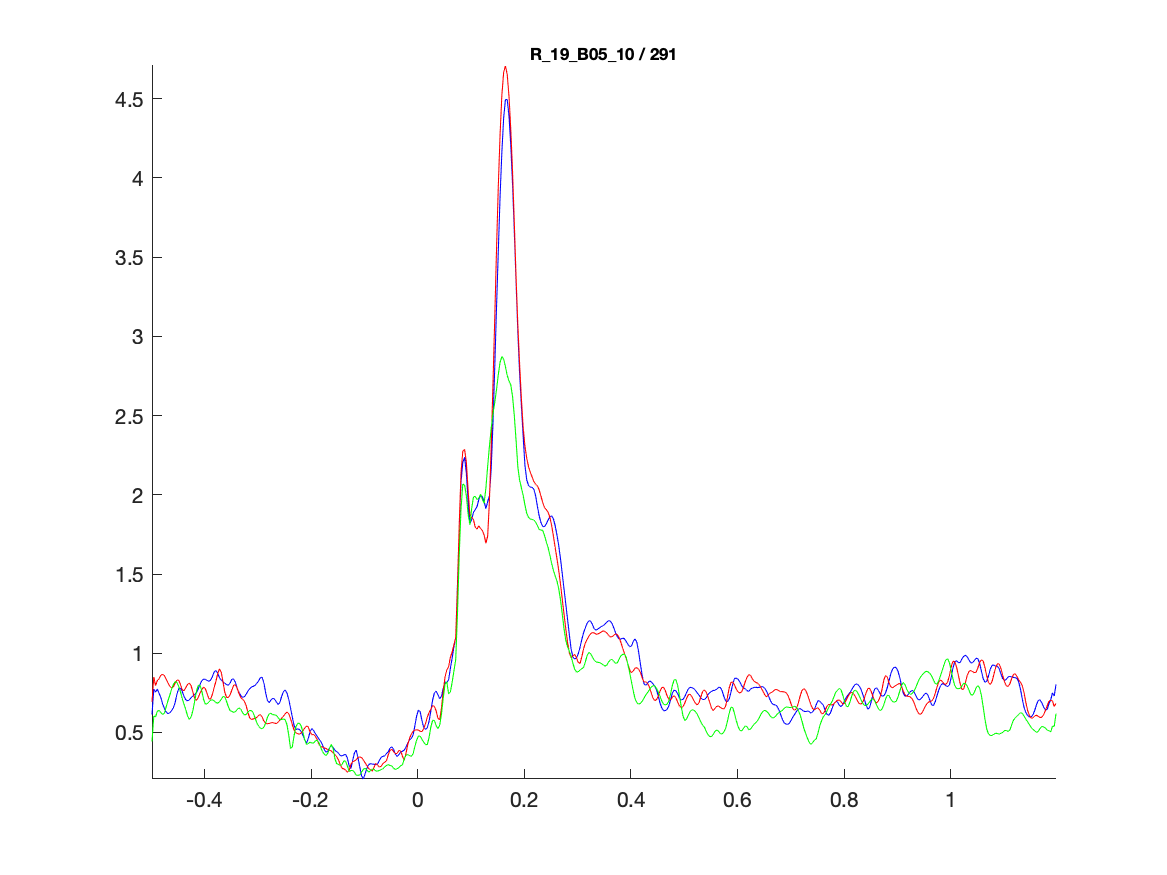
Channel/parcel number 291 has a clear ERP, which is different between the face conditions and the scrambled condition. Let us look at this channel in more detail:
cfg = [];
cfg.channel = 291;
ft_singleplotER(cfg, grandavg_famous, grandavg_unfamiliar, grandavg_scrambled);
Note that you can also very easily make this figure using the standard MATLAB plot function.
Figure; Comparing the ERPs on the virtual channel (parcel) of interest
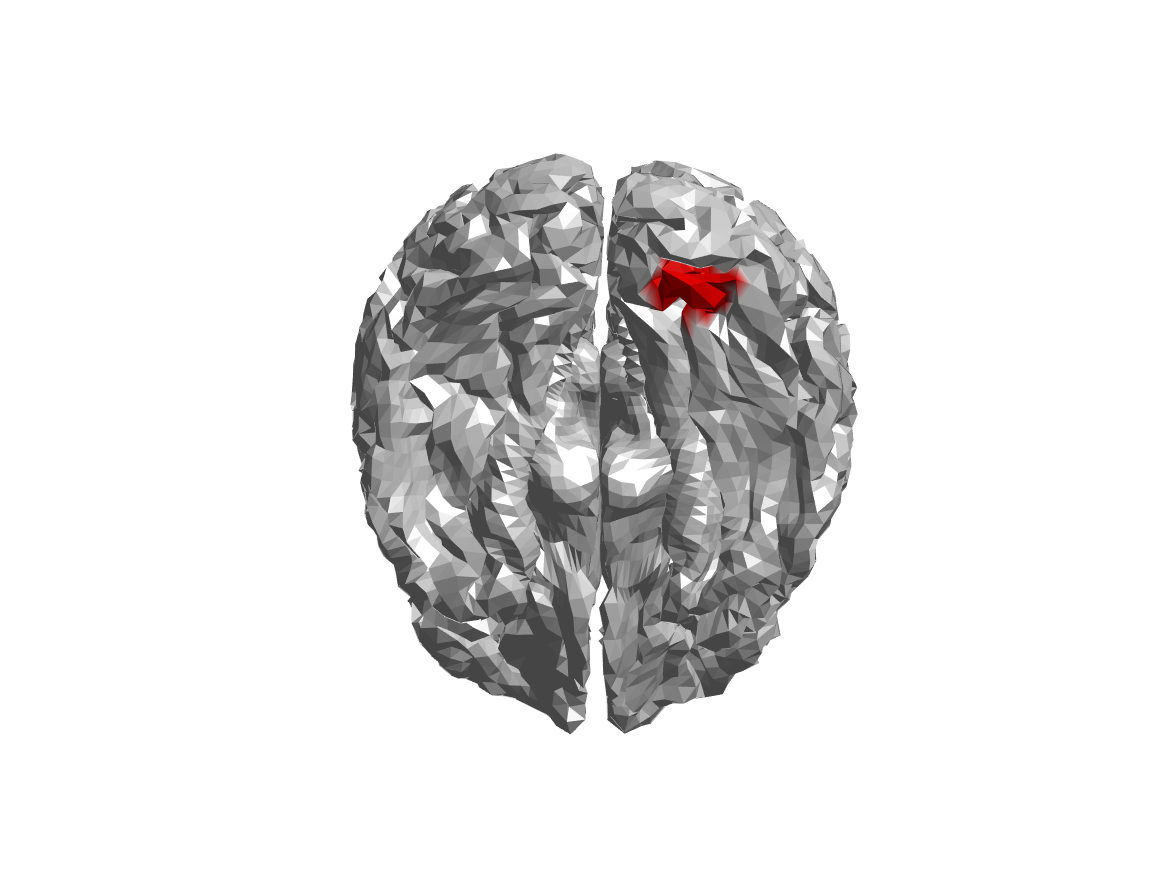
We can use the brainordinate field of one of the subjects to determine where the parcel is located on the cortical sheet:
chan = 291;
brainordinate = avg_scrambled{1}.brainordinate;
color = ones(length(brainordinate.parcellation), 3) * 0.9; % light grey
color(brainordinate.parcellation==chan, 1) = 1; % red
color(brainordinate.parcellation==chan, 2) = 0;
color(brainordinate.parcellation==chan, 3) = 0;
% all vertices are grey, except for the ones that belong to the parcel of interest
ft_plot_mesh(brainordinate, 'vertexcolor', color)
view(0, -45)
camlight
Figure; Location of the parcel corresponding to the virtual channel of interest
We will continue with a single parcel here. However, there is no reason to assume that the effect of face recognition is lateralized to the right, so a better approach might be to average the corresponding parcels in both hemispheres.
From the grand average plot we can zoom in on our comparison of interest and only plot the ERF of channel/parcel 291 for all subjects, using the individual subject averaged data.
chan = 291;
time = [0.150 0.200];
% Scaling of the vertical axis for the plots below
ymax = 10;
figure;
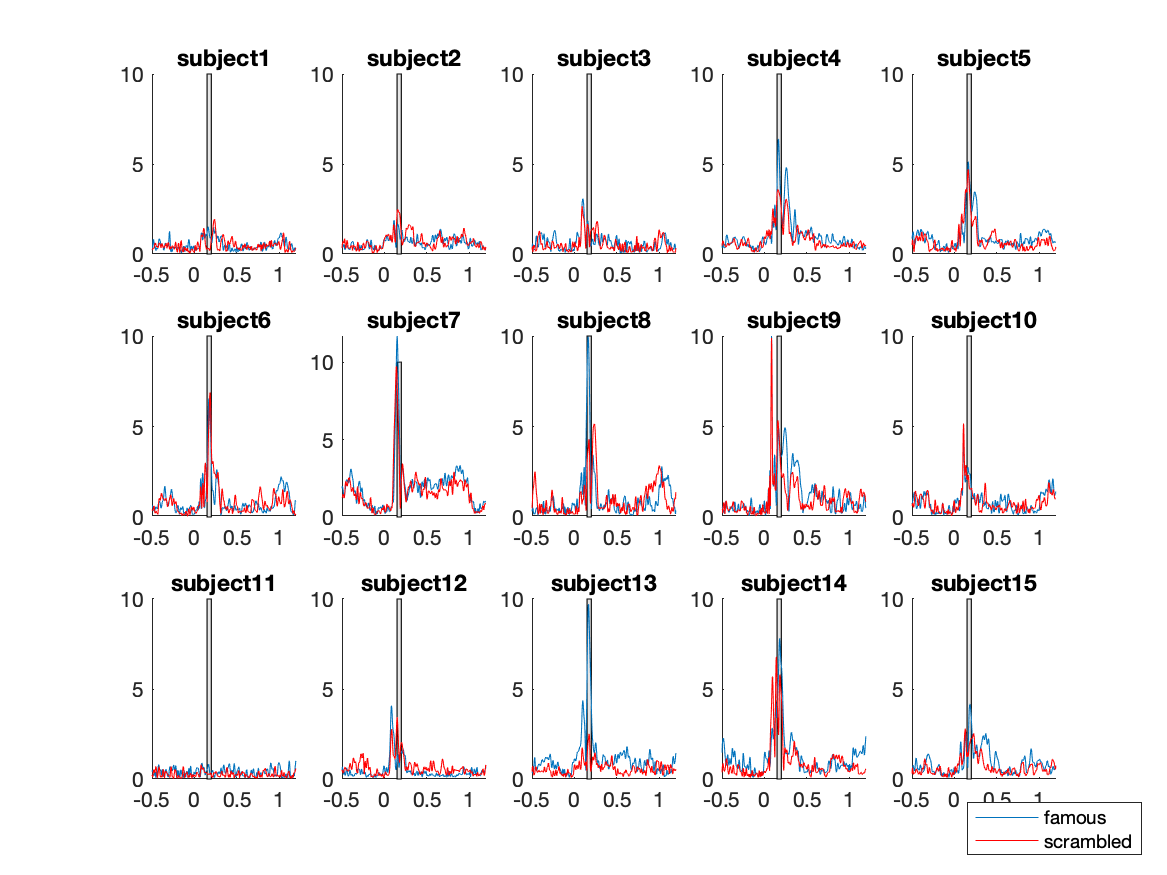
for iSub = 1:numel(subj)
subplot(3, 5, iSub)
% use the rectangle to indicate the time range used later
rectangle('Position', [time(1) 0 (time(2)-time(1)) ymax], 'FaceColor', [1 1 1]*0.9);
hold on;
% plot the lines in front of the rectangle
plot(avg_famous{iSub}.time, avg_famous{iSub}.avg(chan, :));
plot(avg_scrambled{iSub}.time, avg_scrambled{iSub}.avg(chan, :), 'r');
title(strcat('subject ', num2str(iSub)))
% ylim([0 ymax])
xlim([-0.5 1.2])
end
legend({'famous', 'scrambled'})
Figure; Single subject results, the time window of interest is highlighted
From the individual plots and the grand average plots above, it appears that between 150ms and 200ms there is a difference between the conditions in channel 291. That should not come as a surprise, it is the N170 component which reflects the neural processing of faces.
We can also plot the differences between conditions, for each subject, in a different manner to further highlight the difference between conditions, using the code below:
% find the data points for the effect of interest in the grand average
chan = 291;
time = [0.150 0.200];
timesel = find(grandavg_famous.time >= time(1) & grandavg_famous.time <= time(2));
% select the individual subject data and calculate the mean
for iSub = 1:numel(subj)
values_famous(iSub) = mean(avg_famous{iSub}.avg(chan, timesel));
values_scrambled(iSub) = mean(avg_scrambled{iSub}.avg(chan, timesel));
end
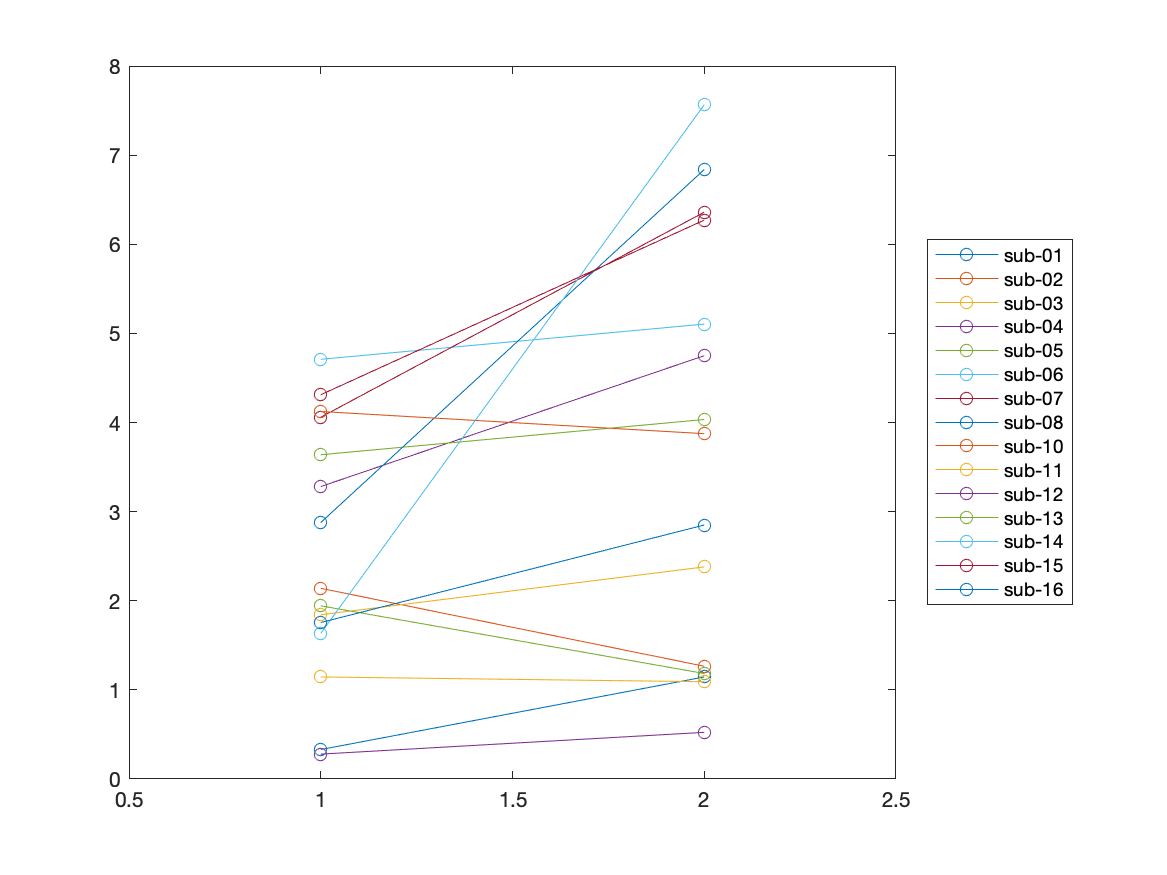
% plot to see the effect in each subject
M = [values_scrambled', values_famous'];
figure; plot(M', 'o-'); xlim([0.5 2.5])
legend({subj.name}, 'location', 'EastOutside');
Figure; Single subject results, averaged for the channel of interest and the time window of interest
We are starting with a single-channel analysis here for purely didactical reasons, i.e. start with a simple test without multiple comparisons, and then build up the complexity by adding multiple time points and parcels.
In practice you should not guide your statistical analysis by a visual inspection of the data; you should state your hypothesis up-front and avoid data dredging or p-hacking.
T-test with MATLAB function
You can do a dependent samples t-test with the MATLAB ttest function (in the Statistics toolbox) where you average over this time window for each condition, and compare the average between conditions. From the output, we look at the output variable ‘stats’ and see that the effect on the selected time and channel is significant with a t-value of 2.4332 and a p-value of 0.029.
% dependent samples ttest
famous_minus_scrambled = values_famous - values_scrambled;
[h, p, ci, stats] = ttest(famous_minus_scrambled, 0, 0.05) % H0: mean = 0, alpha 0.05
T-test with FieldTrip function
You can do the same thing in FieldTrip (which does not require the statistics toolbox) using the ft_timelockstatistics function. This should give you the same p-value.
% define the parameters for the statistical comparison
cfg = [];
cfg.channel = 291;
cfg.latency = [0.150 0.200];
cfg.avgovertime = 'yes';
cfg.parameter = 'avg';
cfg.method = 'analytic';
cfg.statistic = 'ft_statfun_depsamplesT';
cfg.alpha = 0.05;
cfg.correctm = 'no';
Nsub = 15;
cfg.design(1, 1:2*Nsub) = [ones(1, Nsub) 2*ones(1, Nsub)];
cfg.design(2, 1:2*Nsub) = [1:Nsub 1:Nsub];
cfg.ivar = 1; % the 1st row in cfg.design contains the independent variable
cfg.uvar = 2; % the 2nd row in cfg.design contains the subject number
stat = ft_timelockstatistics(cfg, avg_famous{:}, avg_scrambled{:}); % don't forget the {:}
From the code above you can see that the statistical comparison is between conditions (famous and scrambled), and that in order to do this you must provide the individual time-locked averages from each subject.
Exercise 1
Look at the temporal evolution of the effect by changing cfg.latency and cfg.avgovertime in ft_timelockstatistics. You can plot the t-value versus time, the probability versus time and the statistical mask versus time. Note that the output of the ft_timelockstatistics function closely resembles the output of the ft_timelockanalysis function.
Multiple comparisons
In the previous paragraph we picked a channel/parcel and time window by hand after eyeballing the effect. If you would like to test the significance of the effect in all channels/parcels, you could make a for-loop over channels.
time = [0.150 0.200];
timesel = find(grandavg_famous.time >= time(1) & grandavg_famous.time <= time(2));
clear h p
famous_minus_scrambled = zeros(1, 15);
% loop over channels
for iChan = 1:374
for iSub = 1:15
famous_minus_scrambled(iSub) = ...
mean(avg_famous{iSub}.avg(iChan, timesel)) - ...
mean(avg_scrambled{iSub}.avg(iChan, timesel));
end
[h(iChan), p(iChan)] = ttest(famous_minus_scrambled, 0, 0.05 ); % test each channel separately
end
% plot uncorrected "significant" channels
cfg = [];
cfg.operation = 'subtract';
cfg.parameter = 'avg';
grandavg_effect = ft_math(cfg, grandavg_famous, grandavg_scrambled);
cfg = [];
cfg.layout = layout;
cfg.colorgroups = 1:374;
cfg.linecolor = ones(374, 3) * 0.5; % light grey
cfg.linecolor(find(h), 1) = 1; % red
cfg.linecolor(find(h), 2) = 0;
cfg.linecolor(find(h), 3) = 0;
cfg.comment = 'no';
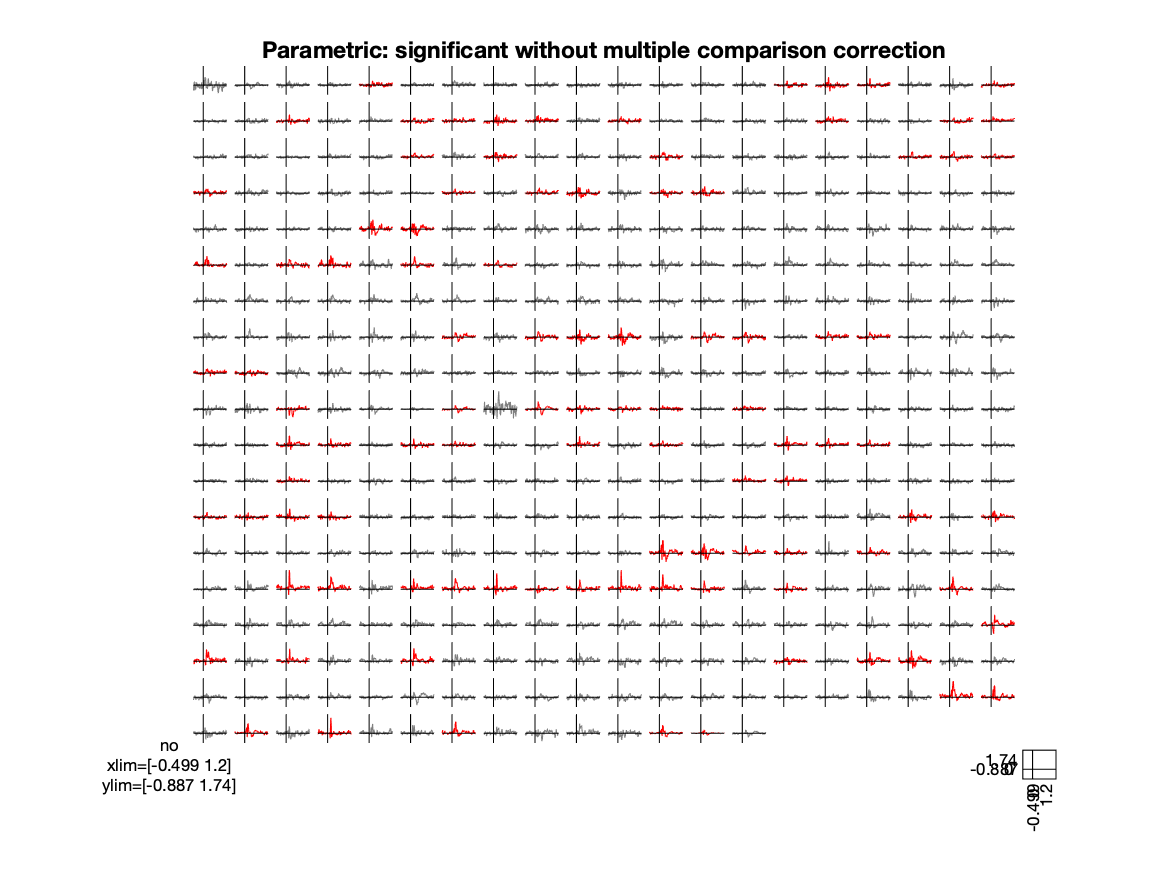
figure; ft_multiplotER(cfg, grandavg_effect)
title('Parametric: significant without multiple comparison correction')
Figure; Parametric test, plot of the effect size with significant channels in red
However, since now you are performing 374 individual tests, you are no longer controlling the false alarm rate. Given the null-hypothesis and an alpha of 5%, you have a 5% chance of making a false alarm in every channel, and incorrectly concluding that the null-hypothesis should be rejected. As the 5% false alarm rate applies to each test that you perform, the chance of making a false alarm for 374 tests at the same time is much larger than the desired 5%. This is the multiple comparison problem.
To ensure that the false alarm rate is controlled at the desired alpha level over all channels, you should do a correction for multiple comparisons. The best known correction is the Bonferroni correction, which controls the false alarm rate for multiple independent tests. To do this, divide your initial alpha level (i.e. the desired upper boundary for the false alarm rate) by the number of tests that you perform. In this case with 374 channels the alpha level would become 0.05/374 which is 0.00013369. With this alpha value the effect is no longer significant on any channel. In some cases, as in this one, a Bonferroni correction is too conservative, because the effect on one channel is highly correlated with neighboring channels (in space, and also in time). In sum, even though the Bonferroni correction achieves the desired control of the type-I error (false alarm rate), the type-II error (chance of not rejecting H0 when in fact it should be rejected) is much larger than desired.
Below you can see the means by which to implement a Bonferroni correction. However, there are other options on FieldTrip to control for multiple comparisons which are less conservative, and hence more sensitive.
Bonferroni correction with MATLAB function
% with Bonferroni correction for multiple comparisons
famous_minus_scrambled = zeros(1, 15);
for iChan = 1:374
for iSub = 1:15
famous_minus_scrambled(iSub) = ...
mean(avg_famous{iSub}.avg(iChan, timesel)) - ...
mean(avg_scrambled{iSub}.avg(iChan, timesel));
end
[h(iChan), p(iChan)] = ttest(famous_minus_scrambled, 0, 0.05/374); % test each channel separately
end
Bonferroni correction with FieldTrip function
cfg = [];
cfg.channel = 'all';
cfg.latency = [0.150 0.200];
cfg.avgovertime = 'yes';
cfg.parameter = 'avg';
cfg.method = 'analytic';
cfg.statistic = 'ft_statfun_depsamplesT';
cfg.alpha = 0.05;
cfg.correctm = 'bonferroni';
Nsub = 15;
cfg.design(1, 1:2*Nsub) = [ones(1, Nsub) 2*ones(1, Nsub)];
cfg.design(2, 1:2*Nsub) = [1:Nsub 1:Nsub];
cfg.ivar = 1; % the 1st row in cfg.design contains the independent variable
cfg.uvar = 2; % the 2nd row in cfg.design contains the subject number
stat_bonferroni = ft_timelockstatistics(cfg, avg_famous{:}, avg_scrambled{:});
FieldTrip also has other methods implemented for performing a multiple comparison correction, such as the FDR. See the ft_statistics_analytic function for the options to cfg.correctm when you are doing a parametric test.
Non-parametric statistics
Permutation test based on t statistics
Instead of using the analytic t-distribution to calculate the appropriate p-value for your effect, you can use a nonparametric randomization test to obtain the p-value.
This is implemented in FieldTrip in the function ft_statistics_montecarlo, which is called by ft_timelockstatistics when you set cfg.method = 'montecarlo'. A Monte-Carlo estimate of the significance probabilities and/or critical values is calculated based on randomizing (or permuting) your data many times between the conditions.
cfg = [];
cfg.channel = 'all';
cfg.latency = [0.150 0.200]; % see below for exercise
cfg.avgovertime = 'yes'; % see below for exercise
cfg.parameter = 'avg';
cfg.method = 'montecarlo';
cfg.statistic = 'ft_statfun_depsamplesT';
cfg.alpha = 0.05;
cfg.correctm = 'no';
cfg.correcttail = 'prob';
cfg.numrandomization = 1000;
Nsub = 15;
cfg.design(1, 1:2*Nsub) = [ones(1, Nsub) 2*ones(1, Nsub)];
cfg.design(2, 1:2*Nsub) = [1:Nsub 1:Nsub];
cfg.ivar = 1; % the 1st row in cfg.design contains the independent variable
cfg.uvar = 2; % the 2nd row in cfg.design contains the subject number
stat_nonparametric = ft_timelockstatistics(cfg, avg_famous{:}, avg_scrambled{:});
% make the plot
cfg = [];
cfg.layout = layout;
cfg.colorgroups = 1:374;
cfg.linecolor = ones(374, 3) * 0.5; % light grey
cfg.linecolor(find(stat_nonparametric.mask), 1) = 1; % red
cfg.linecolor(find(stat_nonparametric.mask), 2) = 0;
cfg.linecolor(find(stat_nonparametric.mask), 3) = 0;
cfg.comment = 'no';
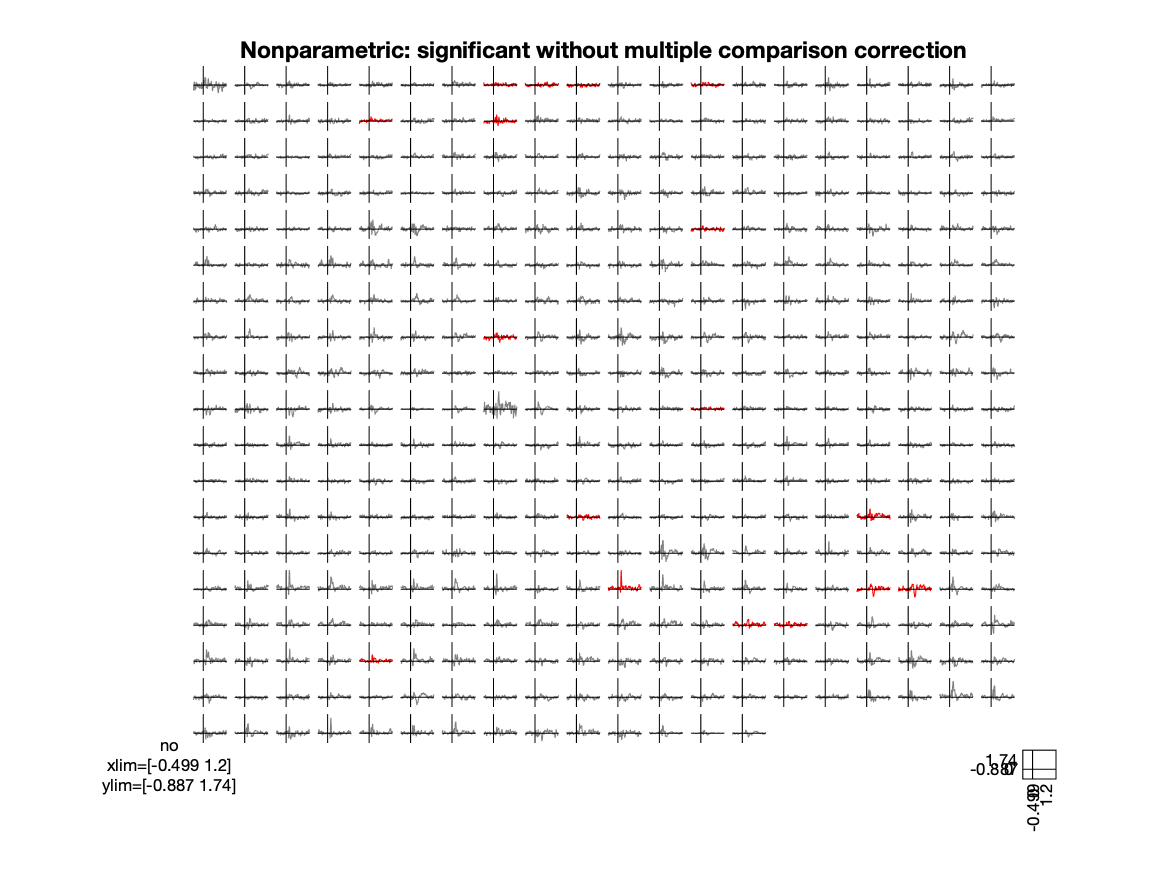
figure; ft_multiplotER(cfg, grandavg_effect)
title('Nonparametric: significant without multiple comparison correction')
Figure; Nonparametric test, plot of the effect size with significant channels in red
Exercise 2
Perform the same statistical test, but now without selecting the time range of interest and without averaging over time. This increases the number of statistical comparisons from Nchan to Nchan x Ntime. The statistics function also returns a Boolean mask that you can use for plotting:
% make the plot
cfg = [];
cfg.layout = layout;
cfg.maskparameter = 'mask';
cfg.maskstyle = 'box';
% we want to plot the effect size,i.e. the difference, but also the statistical mask
grandavg_effect.mask = stat_nonparametric.mask;
figure; ft_multiplotER(cfg, grandavg_effect)
title('Nonparametric: significant without MCP for channels and time')
Also in the non-parametric approach for testing of statistical significance, different corrections for multiple comparisons such as Bonferroni, FDR, and others are implemented. See the options for cfg.correctm in ft_statistics_montecarlo.
Permutation test based on cluster statistics
FieldTrip also implements a special way to correct for multiple comparisons, which makes use of the feature in the data that the effects at neighbouring timepoints are highly correlated. For more details see the cluster permutation tutorials for ERFs and time frequency data and the publication by Maris and Oostenveld (2007).
If your channels in the data are close to each other, you can also use the feature that neighbouring channels are likely to show similar effects. This requires that you specify which channels are neighbours, see ft_prepare_neighbours. In this case we will not assume that neighbouring patches see the same thing, and will only rely on clustering over the time axis.
cfg = [];
cfg.channel = 'all';
cfg.neighbours = []; % no channel neighbours, only time
cfg.parameter = 'avg';
cfg.method = 'montecarlo';
cfg.statistic = 'ft_statfun_depsamplesT';
cfg.alpha = 0.05;
cfg.correctm = 'cluster';
cfg.correcttail = 'prob';
cfg.numrandomization = 500;
Nsub = 15;
cfg.design(1, 1:2*Nsub) = [ones(1, Nsub) 2*ones(1, Nsub)];
cfg.design(2, 1:2*Nsub) = [1:Nsub 1:Nsub];
cfg.ivar = 1; % the 1st row in cfg.design contains the independent variable
cfg.uvar = 2; % the 2nd row in cfg.design contains the subject number
cfg.spmversion = 'spm12';
stat_cluster = ft_timelockstatistics(cfg, avg_famous{:}, avg_scrambled{:});
% make a plot
cfg = [];
cfg.layout = layout;
cfg.maskparameter = 'mask';
cfg.maskstyle = 'box';
grandavg_effect.mask = stat_cluster.mask;
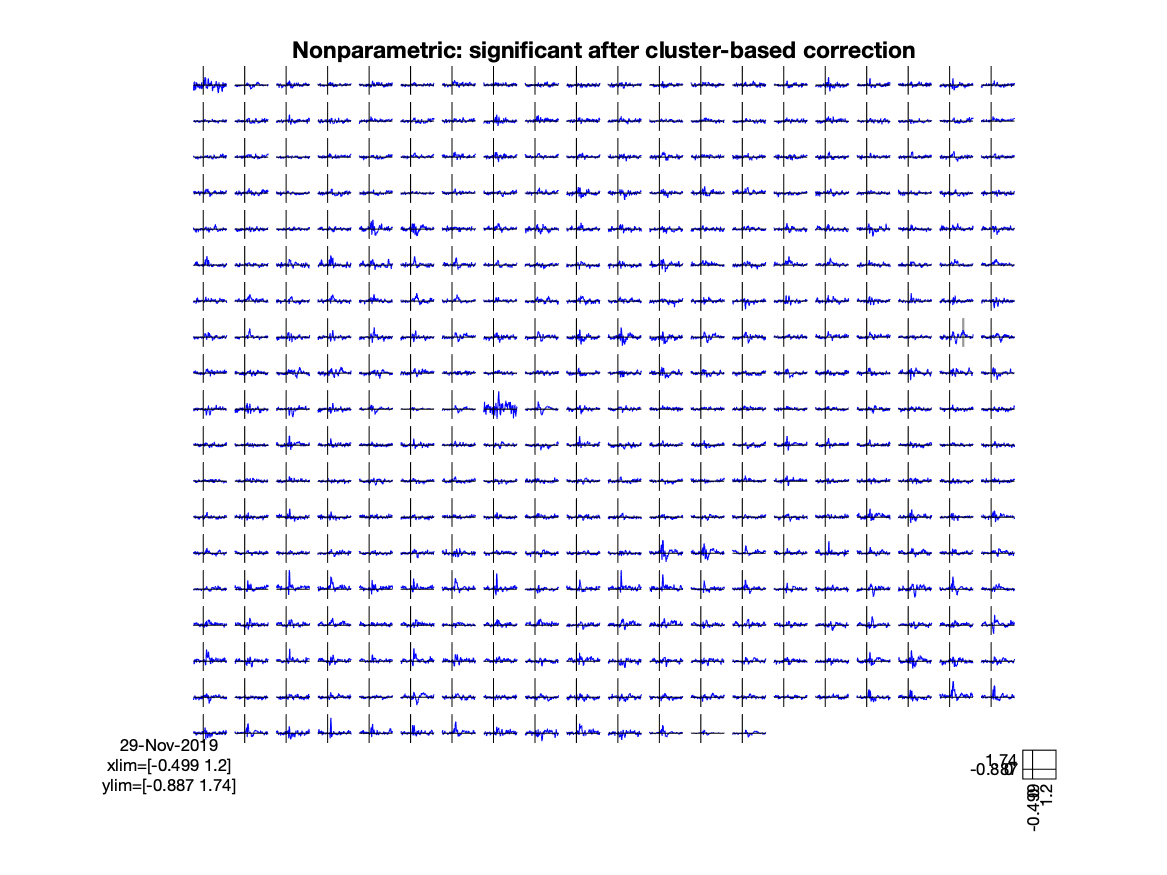
figure; ft_multiplotER(cfg, grandavg_effect)
title('Nonparametric: significant after cluster-based correction')
Figure; Nonparametric test, cluster-based correction for multiple comparisons
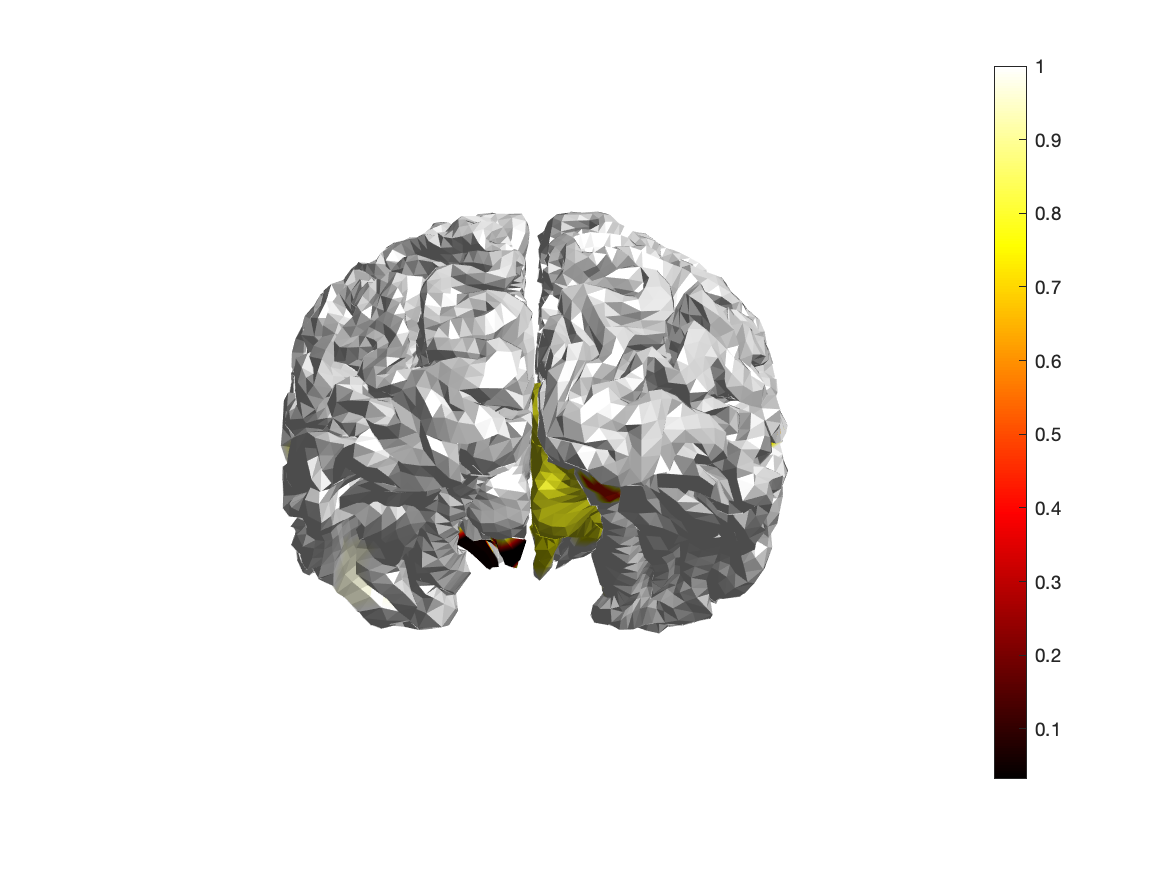
Although a single test is performed to test exchangeability of the whole data over conditions, each data element (channel time point) can be assigned to a cluster, and for each cluster the likelihood of observing the cluster-mass under the H0 is computed. You can visualize the spatial distribution of probabilities on the parcels that together form the cortical sheet.
brainordinate = avg_scrambled{1}.brainordinate;
% we take the minimum value (over time) for each channel
% and compute the -log10(), which causes 10% to be mapped onto 1, 1% onto 2, etc.
% the threshold of 5% corresponds to a log-transformed value of 1.3
color = -log10(min(stat_cluster.prob, [], 2));
color = nan(size(brainordinate.pos,1),1);
for i=1:374
color(brainordinate.parcellation==i) = min(stat_cluster.prob(i,:),[],2);
end
ft_plot_mesh(brainordinate, 'vertexcolor', color)
view(0, -45)
colormap('hot')
colorbar
camlight
Figure; Spatial distribution of p-values over the parcels
Exercise 3
Explain why the results of the cluster-based permutation test are not showing the same as the statistical tests for the region of interest and/or the time window of interest. What can you learn from the outcome of this statistical test?
Although the distribution of the p-values can be informative to learn something about the distribution of the effect, the decision to reject the null-hypothesis is only based on the “largest” cluster, i.e. the most unlikely piece of evidence that you have against the H0.
To properly write up your results in a manuscript, you should check the guidelines on how NOT to interpret results from a cluster-based permutation test.