Beamforming oscillatory responses in combined MEG/EEG data
Introduction
In this tutorial we will continue working on the dataset described in the preprocessing tutorials. Below we will repeat code to select the trials and preprocess the data as described in the earlier tutorials (trigger-based trial selection, visual artifact rejection).
In this tutorial you will learn about applying beamformer techniques in the frequency domain. You will learn how to compute appropriate time-frequency windows, an appropriate head model and lead field matrix, and various options for contrasting the effect of interest against some control/baseline. Finally, you will be shown several options for plotting the results overlaid on a structural MRI.
It is expected that you understand the previous steps of preprocessing and filtering the sensor data. Some understanding of the options for computing the head model and forward lead field is also useful.
This tutorial will not cover the time-domain option for LCMV/SAM beamformers (described in Background), nor for beamformers applied to evoked/averaged data (although see an example of how to calculate virtual sensors using LCMV for an example of this).
This tutorial contains the hands-on material of the NatMEG workshop and is complemented by this lecture.
Background
In the Time-Frequency Analysis tutorial we identified strong oscillations in the beta band in a motor response paradigm. The goal of this section is to identify the sources responsible for producing this oscillatory activity. We will apply a beamformer technique. This is a spatially adaptive filter, allowing us to estimate the amount of activity at any given location in the brain. The inverse filter is based on minimizing the source power (or variance) at a given location, subject to ‘unit-gain constraint’. This latter part means that, if a source had power of amplitude 1 and was projected to the sensors by the lead field, the inverse filter applied to the sensors should then reconstruct power of amplitude 1 at that location. Beamforming assumes that sources in different parts of the brain are not temporally correlated.
The brain is divided in a regular three dimensional grid and the source strength for each grid point is computed. The method applied in this example is termed Dynamical Imaging of Coherent Sources (DICS) and the estimates are calculated in the frequency domain (Gross et al. 2001). Other beamformer methods rely on source estimates calculated in the time domain, e.g., the Linearly Constrained Minimum Variance (LCMV) and Synthetic Aperture Magnetometry (SAM) methods (van Veen et al., 1997; Robinson and Cheyne, 1997). These methods produce a 3D spatial distribution of the power of the neuronal sources. This distribution is then overlaid on a structural image of the subject’s brain. Furthermore, these distributions of source power can be subjected to statistical analysis. It is always ideal to contrast the activity of interest against some control/baseline activity. Options for this will be discussed below, but it is best to keep this in mind when designing your experiment from the start, rather than struggle to find a suitable control/baseline after data collection.
Procedure
To localize the oscillatory sources for the example dataset we will perform the following steps:
- Reading in the subject specific anatomical MRI using ft_read_mri
- Construct a forward model using ft_volumesegment and ft_prepare_headmodel
- Prepare the source model using ft_prepare_sourcemodel
Next, we head out to investigate the response to the finger movement. We will localize the sources of the motor beta-band activity following the following step
- Load the data from disk and define baseline and poststimulus period using ft_redefinetrial
- Compute the cross-spectral density matrix for all MEG channels using the function ft_freqanalysis
- Compute the lead field matrices using ft_prepare_leadfield
- Compute a common spatial filter and estimate the power of the sources using ft_sourceanalysis
- Compute the condition difference
- Visualize the result with ft_sourceplot
Note that some of the steps will be skipped in this tutorial as we have already done them in the previous days of the workshop.
Figure: An example of a pipeline to locate oscillatory sources.
Preparing the data and the forward and inverse model
Loading the data
First, we are going to load the data already preprocessed during the Time-frequency analysis tutorial.
Load the data using the following command:
load data_clean_MEG_responselocked.mat
Loading the headmodel
The first requirement for the source reconstruction procedure is that we need a forward model. The forward model allows us to calculate the distribution of the magnetic field on the MEG sensors given a hypothetical current distribution. We are going to use the forward model that was calculated in the dipole fitting tutorial.
Load the forward model using the following code:
load headmodel_meg.mat
Identifying a time window of interest
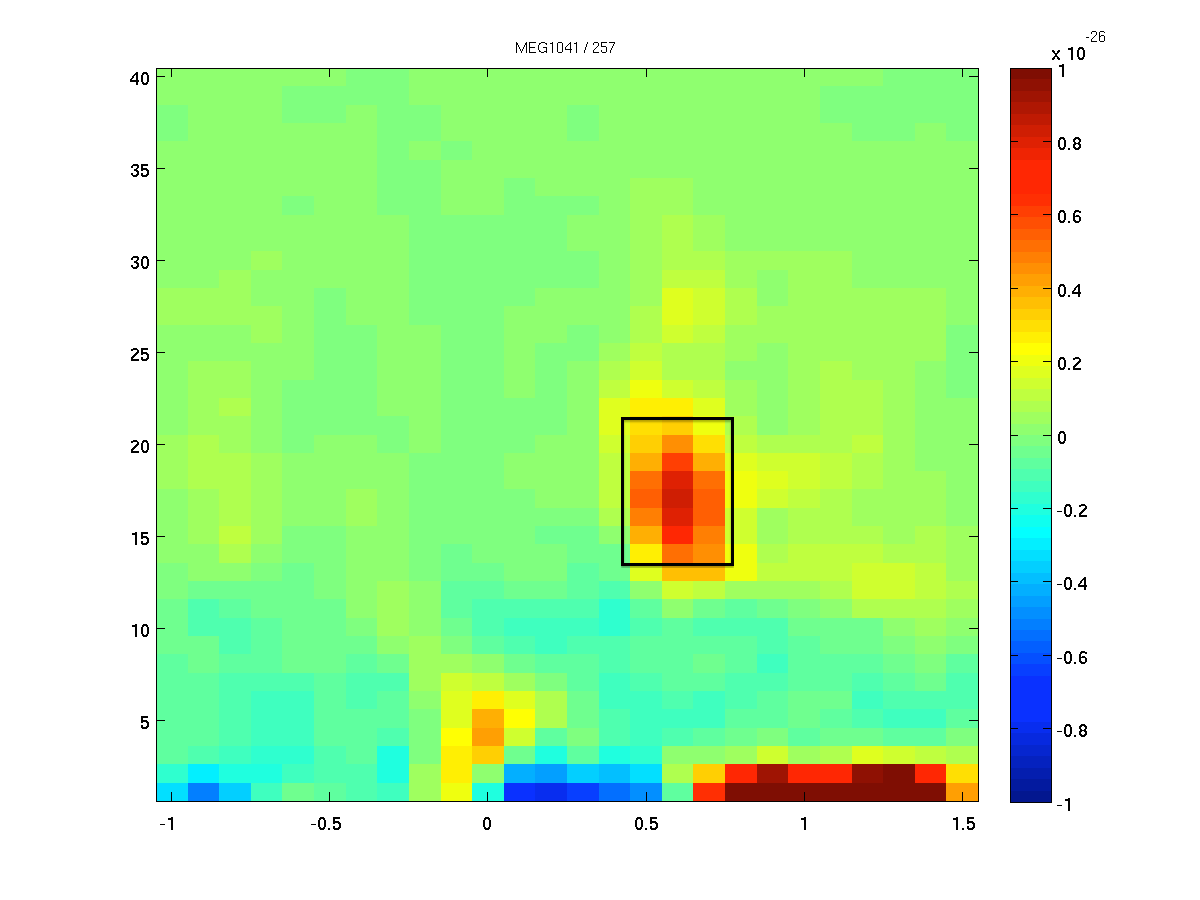
The aim is to identify the sources of oscillatory activity in the beta band. From the section time-frequency analysis we have identified 18 Hz as the center frequency for which the power estimates should be calculated. We seek to compare the activation between the response with the left finger to the activation in response to the right finger. We first use ft_preprocessing and ft_redefinetrial to extract relevant data. It is important that the length of each data piece is the length of a fixed number of oscillatory cycles. Here 9 cycles are used resulting in a 9/18 Hz = 0.5 s time window. Thus, the time window we will use ranges from 0.35 to 0.85 second after response onset (see Figure 2).
Figure: The time-frequency presentation used to determine the time- and frequency-windows prior to beamforming.
Now we select the time windows of interest, the post-response window using ft_redefinetrial.
% Select time window of interest
cfg = [];
cfg.toilim = [0.35 0.85];
data_timewindow = ft_redefinetrial(cfg,data_clean_MEG_responselocked);
As mentioned in the Background, it is ideal to contrast the activity of interest against some control.
- Suitable control windows are, for example
- Activity contrasted with baseline (example not shown)
- Activity of condition 1 contrasted with condition 2 (example shown here using left vs right)
- However, if no other suitable data condition or baseline time-window exists, then
- Activity contrasted with estimated noise (example shown below)
- Use normalized leadfields
The null hypothesis for both options within (1) is that the data in both conditions are the same, and thus the best spatial filter is the one that is computed using both data conditions together (also known as ‘common filters’). This common filter is then applied separately to each condition. To calculate the common filter, we will use the extracted time window pooled over both conditions.
Exercise 1: data length
Why is it important that the length of each data piece is the length of a fixed number of oscillatory cycles?
Exercise 2: common filter data
Why shouldn’t we calculate a spatial filter for both conditions separately in this case? Would there be a reason to do so?
(MEG) Calculating the cross spectral density matrix
The beamformer technique is based on an adaptive spatial filter. The DICS spatial filter is derived from the frequency counterpart of the covariance matrix: the cross-spectral density matrix. This matrix contains the cross-spectral densities for all sensor combinations and is computed from the Fourier transformed data of the single trials. It is given as output when cfg.output = ‘powandcsd’. The frequency of interest is 18 Hz and the smoothing window is +/- 4 Hz:
% Freqanalysis for beamformer
cfg = [];
cfg.channel = {'MEG*2', 'MEG*3'};
cfg.method = 'mtmfft';
cfg.taper = 'dpss';
cfg.output = 'powandcsd';
cfg.keeptrials = 'no';
cfg.foi = 18;
cfg.tapsmofrq = 4;
% for common filter over conditions
powcsd_all = ft_freqanalysis(cfg, data_timewindow);
% for conditions
cfg.trials = find(data_timewindow.trialinfo(:,1) == 256);
powcsd_left = ft_freqanalysis(cfg, data_timewindow);
cfg.trials = find(data_timewindow.trialinfo(:,1) == 4096);
powcsd_right = ft_freqanalysis(cfg, data_timewindow);
The cross-spectral density data structure has a similar data structure as other output out of ft_freqanalysis:
powcsd_all =
label: {204x1 cell} % Channel labels
dimord: 'chan_freq' % Dimensions in the data
freq: 17.8571 % Target frequency
powspctrm: [206x1 double] % Power spectrum
labelcmb: {20706x2 cell} % Channel combinations
crsspctrm: [20706x1 double] % Cross-spectral density matrix
elec: [1x1 struct] % EEG electrode information
grad: [1x1 struct] % MEG sensor information
cfg: [1x1 struct] % Configuration
How come our target frequency is 17.8657, didn’t we ask for 18? Hint: How large is our time window?
Compute lead field
The next step is to discretize the brain volume into a grid. For each grid point the lead field matrix is calculated. It is calculated with respect to a grid with a 0.5 cm resolution.
Sensors that were previously removed from the data set should also be removed when calculating the leadfield.
As mentioned earlier on, if you are not contrasting the activity of interest against another condition or baseline time-window, then you may choose to normalize the lead field (cfg.normalize=’yes’), which will help control against the power bias towards the center of the head.
% Create source model with leadfields
cfg = [];
cfg.channel = {'MEG*2', 'MEG*3'};
cfg.grad = powcsd_all.grad;
cfg.headmodel = headmodel_meg;
cfg.dics.reducerank = 2; % default for MEG is 2, for EEG is 3
cfg.resolution = 0.5; % use a 3-D grid with a 0.5 cm resolution
cfg.unit = 'cm';
cfg.tight = 'yes';
[grid] = ft_prepare_leadfield(cfg);
The source model has the following fields:
grid =
xgrid: [1x26 double] % X-axis grid
ygrid: [1x36 double] % Y-axis grid
zgrid: [1x28 double] % Z-axis grid
dim: [26 36 28] % Size of the dimensions in the grid
pos: [26208x3 double] % 3d coordinates of every position in the grid
unit: 'cm' % Units of the coordinates in the grid
inside: [1x13308 double] % Grid points inside the brain
outside: [1x12900 double] % Grid points outside the bain
cfg: [1x1 struct] % Configuration
leadfield: {1x26208 cell} % Leadfield for every position in grid
(MEG) Source analysis on conditions
Using the cross-spectral density and the lead field matrices a spatial filter is calculated for each grid point. By applying the filter to the Fourier transformed data we can then estimate the power for the pre- and post-stimulus activity. This results in a power estimate for each grid point. Since we want to use a common filter, we first need to input data from all conditions:
cfg = [];
cfg.channel = {'MEG*2', 'MEG*3'};
cfg.method = 'dics';
cfg.frequency = 18;
cfg.grid = grid;
cfg.headmodel = headmodel_meg;
cfg.senstype = 'MEG'; % Must me 'MEG', although we only kept MEG channels, information on EEG channels is still present in data
cfg.dics.keepfilter = 'yes'; % We wish to use the calculated filter later on
cfg.dics.projectnoise = 'yes';
cfg.dics.lambda = '5%';
source_all = ft_sourceanalysis(cfg, powcsd_all);
The source data structure has the following fields:
source_all =
dim: [26 36 28] % Dimensions of the data
freq: 18.1159 % Target frequency
pos: [26208x3 double] % 3d-coordinates of the points in the source estimate
inside: [1x13308 double] % Positions inside the brain
outside: [1x12900 double] % Positions outside the brain
method: 'average' % Operation applied over trials
avg: [1x1 struct] % Average power for each point in the source estimate
cfg: [1x1 struct] % Configuration
The purpose of lambda is discussed in Exercise 6. By using cfg.keepfilter = ‘yes’, we let ft_sourceanalysis return the filter matrix in the source structure.
Plotting sources of oscillatory beta-band activity
When plotting the source-level power now, you would realize that the power is strongest in the center of the brain. As already mentioned, there are several ways of circumventing the noise bias towards the center of the head. The most intuitive approach is to contrast two conditions, which may also both experimental conditions as we are dealing with here.
Remember that we intended to contrast the left hand to the right hand responses. Therefore, we need to estimate activity on the source level for the experiment data using the filter obtained from beaming data from both conditions (‘common filter’):
cfg = [];
cfg.channel = {'MEG*2', 'MEG*3'};
cfg.method = 'dics';
cfg.frequency = 18;
cfg.grid = grid;
cfg.sourcemodel.filter = source_all.avg.filter;
cfg.headmodel = headmodel_meg;
cfg.senstype ='MEG';
source_left = ft_sourceanalysis(cfg, powcsd_left);
source_right = ft_sourceanalysis(cfg, powcsd_right);
After successfully applying the above steps, we obtained an estimate of the beta-band suppression in both experimental conditions at each grid point in the brain volume. The grid of estimated power values can be plotted superimposed on the anatomical MRI. This requires the output of ft_sourceanalysis to match position of the MRI. The function ft_sourceinterpolate aligns the source level activity with the structural MRI. We only need to specify what parameter we want to interpolate and to specify the MRI we want to use for interpolation.
First we will load the MRI. It is important that you use the MRI realigned with the sensor or your source activity data will not match the anatomical data. We will load the realigned MRI from the dipole fitting tutorial.
load mri_realigned2.mat
Before aligning the source activity to the MRI we will reslice the MRI using ft_volumereslice. The consequence of this reslicing is that the size of the MRI is decreased (it is rather large now) and the axis are adjusted so that the image is plotted correctly. If your MRI image is plotted upside-down, try using ft_volumereslice.
mri_resliced = ft_volumereslice([], mri_realigned2);
Now we will align the source activity to the MRI:
cfg = [];
cfg.parameter = 'pow';
source_left_int = ft_sourceinterpolate(cfg, source_left, mri_resliced);
source_right_int = ft_sourceinterpolate(cfg, source_right, mri_resliced);
Now we can finally compute the difference between the two conditions. Here we take the ratio between the two conditions normalised by the sum. In this operation we assume that the noise bias is the same for both experimental conditions and it will thus cancel out when contrasting.
source_diff_int = source_left_int;
source_diff_int.pow = (source_left_int.pow - source_right_int.pow) ./ (source_left_int.pow + source_right_int.pow);
Now, we can plot the interpolated data:
cfg = [];
cfg.method = 'ortho';
cfg.funparameter = 'pow';
cfg.funcolorlim = 'maxabs';
cfg.opacitylim = [0 1e-4];
cfg.opacitymap = 'rampup';
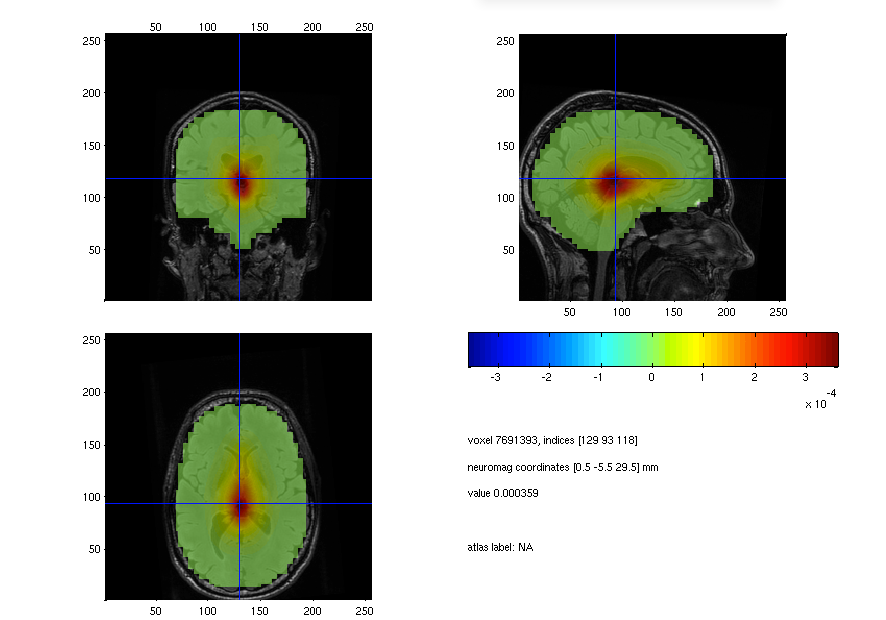
ft_sourceplot(cfg, source_left_int);
Figure: Source plot of the beta response in the left-hand condition.
As you can see the strongest motor response is located in the center of the head. Can you explain this finding?
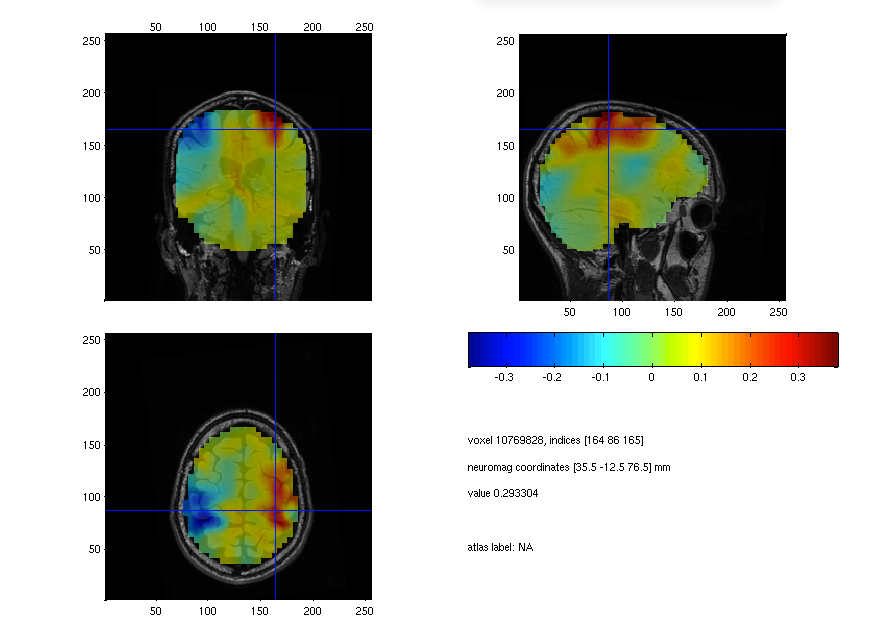
cfg.location = [35 -13 76];
ft_sourceplot(cfg, source_diff_int);
Figure: Source plot of the beta response ratio between the left- and right-hand conditions.
Try to explain the location of the red and blue blobs.
The ‘ortho’ method is not the only plotting method implemented. Use the ‘help’ of ft_sourceplot to find what other methods there are and plot the source level results. What are the benefits and drawbacks of these plotting routines?
Exercise: determining anatomical labels
If you were to name the anatomical label of the source of this motor beta, what you say? What plotting method is most appropriate for this?
With the use of cfg.atlas you can specify a lookup atlas, which ft_sourceplot will use to return appropriate anatomical labels. One for the MNI template is distributed with FieldTrip and can be found in ‘fieldtrip/template/atlas/aal/ROI_MNI_V4.nii’. Be aware that for this to work you need to realign your anatomical and functional data into MNI coordinates. An example how to achieve this is to align the leadfield grid of the individual subject to a leadfield grid in MNI space.
Exercise: regularization
The regularization parameter was lambda = ‘5%’. Change it to ‘0%’ or to ‘10%’ and plot the power estimate. How does the regularization parameter affect the properties of the spatial filter?
(EEG) The forward model and lead field matrix
We will continue to analyze the EEG data according to a series of steps similar to the MEG. Try to note the differences between analyzing the EEG and MEG data.
EEG Head model & data
As before, we will use the head model calculated in the dipole fitting tutorial and the preprocessed data from the time-frequency analysis tutorial.
Load the EEG head model and preprocessed data using the following code:
load headmodel_eeg.mat
load data_clean_EEG_responselocked.mat
(EEG) Calculating the cross spectral density matrix
As before, we are first going to extract a time window that we are interested in using ft_definetrial. Remember that we should extract a window that is a full-length of cycles of our frequency of interest.
% select time window
cfg = [];
cfg.toilim = [0.35 0.85];
data_timewindow = ft_redefinetrial(cfg,data_clean_EEG_responselocked);
Now that we have extracted the time window of interest we can continue with calculating the cross-spectral density matrix:
% Freqanalysis for beamformer
cfg = [];
cfg.method = 'mtmfft';
cfg.taper = 'dpss';
cfg.output = 'powandcsd';
cfg.keeptrials = 'no';
cfg.foi = 18;
cfg.tapsmofrq = 4;
% for common filter over conditions and full duration
powcsd_all = ft_freqanalysis(cfg, data_timewindow);
% for conditions
cfg.trials = find(data_timewindow.trialinfo(:,1) == 256);
powcsd_left = ft_freqanalysis(cfg, data_timewindow);
cfg.trials = find(data_timewindow.trialinfo(:,1) == 4096);
powcsd_right = ft_freqanalysis(cfg, data_timewindow);
(EEG) Lead field calculation
The leadfield is calculated using ft_prepare_leadfield.
% common grid/filter
cfg = [];
cfg.elec = powcsd_all.elec;
cfg.headmodel = headmodel_eeg;
cfg.reducerank = 3; % default is 3 for EEG, 2 for MEG
cfg.resolution = 0.5; % use a 3-D grid with a 0.5 cm resolution
cfg.unit = 'cm';
cfg.tight = 'yes';
[grid] = ft_prepare_leadfield(cfg);
(EEG) Source analysis
Now that we have everything prepared we can start to calculate the common filter through which we we project the data from both conditions.
% beamform common filter
cfg = [];
cfg.method = 'dics';
cfg.frequency = 18;
cfg.grid = grid;
cfg.headmodel = headmodel_eeg;
cfg.senstype = 'EEG'; % Remember this must be specified as either EEG, or MEG
cfg.dics.keepfilter = 'yes';
cfg.dics.lambda = '15%';
source_all = ft_sourceanalysis(cfg, powcsd_all);
How does the value for lambda set here compare to the one for the MEG dataset? Why do you think it is different?
Finally, we can apply source analysis on the separate conditions using the common filter calculated previously.
% beamform conditions
cfg = [];
cfg.method = 'dics';
cfg.frequency = 18;
cfg.grid = grid;
cfg.sourcemodel.filter = source_all.avg.filter; % Use the common filter
cfg.headmodel = headmodel_eeg;
cfg.senstype = 'EEG';
source_left = ft_sourceanalysis(cfg, powcsd_left);
source_right = ft_sourceanalysis(cfg, powcsd_right);
Let’s now see how our sources look like. We will again have to realign our functional data to our anatomical data. We will therefore use the realigned mri from the dipole fitting tutorial which we already loaded and resliced during the MEG section of this tutorial.
The realignment is done using the following cod
cfg = [];
cfg.parameter = 'pow';
source_left_int = ft_sourceinterpolate(cfg, source_left, mri_resliced);
source_right_int = ft_sourceinterpolate(cfg, source_right, mri_resliced);
Next we will calculate the ratio between the left- and right-hand response
source_diff_int = source_left_int;
source_diff_int.pow = (source_left_int.pow - source_right_int.pow) ./ (source_left_int.pow + source_right_int.pow);
Finally, we can plot the data:
cfg = [];
cfg.method = 'ortho';
cfg.funparameter = 'pow';
cfg.funcolorlim = 'maxabs';
ft_sourceplot(cfg, source_left_int);
Figure: An EEG-source plot of the beta response in the left-hand condition.
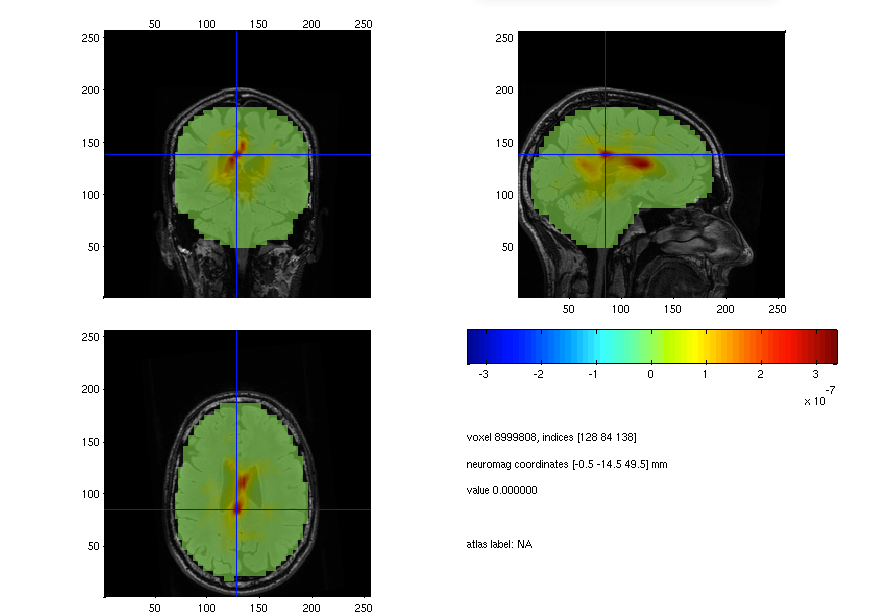
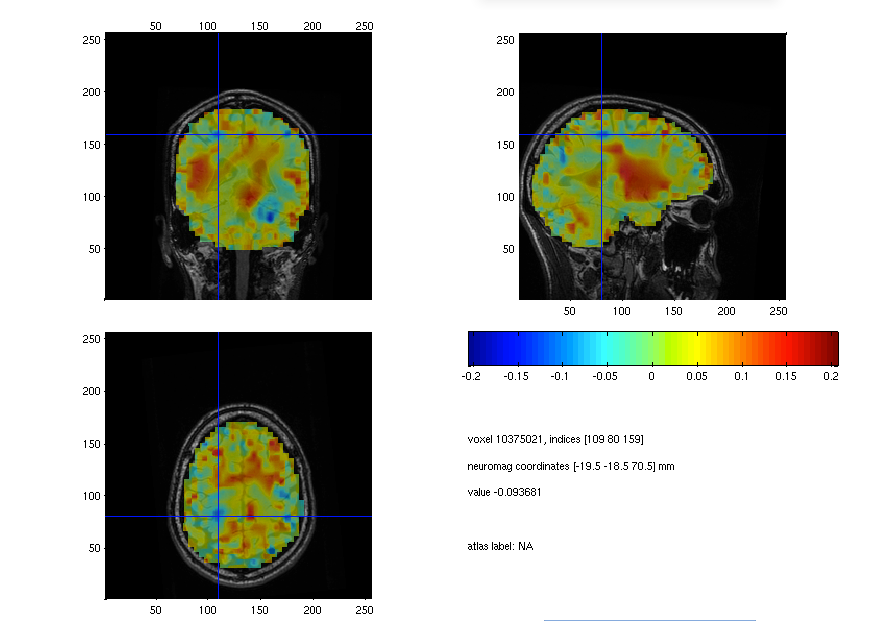
cfg.location = [-19.5 -18.5 70.5];
ft_sourceplot(cfg, source_diff_int);
Figure: An EEG-source plot of ratio of the beta response in the left versus the right hand condition.
How well can you identify the source of the beta-response ration in the EEG source reconstruction? The image seems quite noisy, could you think of a way to enhance the image?
Figure: A MEG-source plot of the beta response in the left versus the right hand condition.
How do the EEG and MEG source plots compare?
If you’ve made it this far, perhaps you could try beamforming a different time window. Looking at the time-frequency plot you might be interested in trying to localise the less obvious beta-band response between 0.75 and 1.25 seconds after response.
Summary and suggested further reading
Beamforming source analysis in the frequency domain with DICS on EEG and MEG data has been demonstrated. Options at each stage and their influence on the results were discussed, such as CSD matrix regularization. Finally, the results were plotted on an orthogonal view.
Computing event-related fields with MNE or LCMV might be of interest. More information on common filters can be found here. If you are doing a group study where you want the grid points to be the same over all subjects, see here. See here for source statistics.
See also these frequently asked questions
- Where is the anterior commissure?
- Can I do combined EEG and MEG source reconstruction?
- Can I restrict the source reconstruction to the grey matter?
- How are the different head and MRI coordinate systems defined?
- How are the Left and Right Pre-Auricular (LPA and RPA) points defined?
- How can I check whether the grid that I have is aligned to the segmented volume and to the sensor gradiometer?
- How can I determine the anatomical label of a source or electrode?
- How can I fine-tune my BEM volume conduction model?
- How can I map source locations onto an anatomical label in an atlas?
- How can I visualize the different geometrical objects that are needed for forward and inverse computations?
- How to coregister an anatomical MRI with the gradiometer or electrode positions?
- Is it good or bad to have dipole locations outside of the brain for which the source reconstruction is computed?
- Is it important to have accurate measurements of electrode locations for EEG source reconstruction?
- What is the conductivity of the brain, CSF, skull and skin tissue?
- What kind of volume conduction models of the head (head models) are implemented?
- Where can I find the dipoli command-line executable?
- Why is there a rim around the brain for which the source reconstruction is not computed?
- Why should I use an average reference for EEG source reconstruction?
See also these examples
- Combined EEG and MEG source reconstruction
- Common filters in beamforming
- Compute forward simulated data using ft_dipolesimulation
- Compute forward simulated data and apply a beamformer scan
- Compute forward simulated data and apply a dipole fit
- Compute forward simulated data with the low-level ft_compute_leadfield
- Check the quality of the anatomical coregistration
- Localizing the sources underlying the difference in event-related fields
- Fit a dipole to the tactile ERF after mechanical stimulation
- Align EEG electrode positions to BEM headmodel
- How to create a head model if you do not have an individual MRI
- How to import data from MNE-Python and FreeSurfer
- Make MEG leadfields using different headmodels
- Plotting the result of source reconstruction on a cortical mesh
- Source statistics
- Create MNI-aligned grids in individual head-space
- Symmetric dipole pairs for beamforming
- Testing BEM created EEG lead fields
- Use your own forward leadfield model in an inverse beamformer computation