Cluster-based permutation tests on event-related fields
Introduction
The objective of this tutorial is to give an introduction to the statistical analysis of event-related EEG and MEG data (denoted as M/EEG data in the following) by means of cluster-based permutation tests. The tutorial starts with a long background section that sketches the background of permutation tests. Subsequently it is shown how to use FieldTrip to perform cluster-based permutation tests on actual axial and planar event-related fields in a between-trials (using single-subject data) and in a within-subjects design (using data from multiple subjects).
In this tutorial we will continue working on the dataset of a single subject described in previous tutorials. Below we will repeat some code to select the trials and preprocess the data as described in the earlier tutorials on Preprocessing - Segmenting and reading trial-based EEG and MEG data, artifact rejection, and Event-related averaging and MEG planar gradient. We assume that the preprocessing and averaging steps of the analysis are already clear for the reader.
This tutorial is not covering statistical test on time-frequency representations. If you are interested in that, you can read the Cluster-based permutation tests on time-frequency data tutorial. If you are interested how parametric statistical tests can be used with FieldTrip, you can read the Parametric and non-parametric statistics on event-related fields tutorial.
This tutorial contains hands-on material that we use for the MEG/EEG toolkit course and it is complemented by this lecture.
Background
The multiple comparisons problem
In the statistical analysis of MEEG-data we have to deal with the multiple comparisons problem (MCP). This problem originates from the fact that MEEG-data are multidimensional. MEEG-data have a spatiotemporal structure: the signal is sampled at multiple channels and multiple time points (as determined by the sampling frequency). The MCP arises from the fact that the effect of interest (i.e., a difference between experimental conditions) is evaluated at an extremely large number of (channel,time)-pairs. This number is usually in the order of several thousands. Now, the MCP involves that, due to the large number of statistical comparisons (one per (channel,time)-pair), it is not possible to control the so called family-wise error rate (FWER) by means of the standard statistical procedures that operate at the level of single (channel,time)-pairs. The FWER is the probability under the hypothesis of no effect of falsely concluding that there is a difference between the experimental conditions at one or more (channel,time)-pairs. A solution of the MCP requires a procedure that controls the FWER at some critical alpha-level (typically, 0.05 or 0.01). The FWER is also called the false alarm rate.
In this tutorial, we describe nonparametric statistical testing of MEEG-data. Contrary to the familiar parametric statistical framework, it is straightforward to solve the MCP in the nonparametric framework. FieldTrip contains a set of statistical functions that provide a solution for the MCP. These are the functions ft_timelockstatistics and ft_freqstatistics which compute significance probabilities using a non-parametric permutation tests. Besides nonparametric statistical tests, ft_timelockstatistics and ft_freqstatistics can also perform parametric statistical tests (see the Parametric and non-parametric statistics on event-related fields tutorial). However, in this tutorial the focus will be on non-parametric testing.
Structure in experiment and data
Different types of data
MEEG-data have a spatiotemporal structure: the signal is sampled at multiple channels and multiple time points. Thus, MEEG-data are two-dimensional: channels (the spatial dimension) X time-points (the temporal dimension). In the following, these (channel,time)-pairs will be called samples. In some studies, these two-dimensional data are reduced to one-dimensional data by averaging over either a selected set of channels or a selected set of time-points.
In many studies, there is an interest in the modulation of oscillatory brain activity. Oscillatory brain activity is measured by power estimates obtained from Fourier or wavelet analyses of single-trial spatiotemporal data. Very often, power estimates are calculated for multiple data segments obtained by sliding a short time window over the complete data segment. In this way, spatio-spectral-temporal data are obtained from the raw spatiotemporal data. The spectral dimension consists of the different frequency bins for which the power is calculated. In the following, these (channel,frequency,time)-triplets will be called samples. In some studies, these three-dimensional data are reduced to one- or two-dimensional data by averaging over a selected set of channels, a selected set of time points, and/or a selected set of frequencies.
Structure in an experiment
The data are typically collected in different experimental conditions and the experimenter wants to know if there is a significant difference between the data observed in these conditions. To answer this question, statistical tests are used. To understand these statistical tests one has to know how the structure in the experiment affects the structure in the data. Two concepts are crucial for describing the structure in an experiment:
- The concept of a unit of observation (UO).
- The concept of a between- or a within-UO design. In M/EEG experiments, there are two types of UO: subjects and trials (i.e., epochs of time within a subject). Concerning the concept of a between- or a within-UO design, there are two schemes according to which the UOs can be assigned to the experimental conditions: (1) every UO is assigned to only one of a number of experimental conditions (between UO-design; independent samples), or (2) every UO is assigned to multiple experimental conditions in a particular order (within UO-design; dependent samples). Therefore, in a between-UO design, there is only one experimental condition per UO, and in a within-UO design there are multiple experimental conditions per UO. These two experimental designs require different test statistics.
The two UO-types (subjects and trials) and the two experimental designs (between- and within-UO) can be combined and this results in four different types of experiments.
Computation of the test statistic and its significance probability
The statistical testing in FieldTrip is performed by the functions ft_timelockstatistics and ft_freqstatistics. From a statistical point of view, the calculations performed by these two functions are very similar. These functions differ with respect to the data structures on which they operate: ft_timelockstatistics operates on data structures produced by ft_timelockanalysis and ft_timelockgrandaverage, and ft_freqstatistics operates on data structures produced by ft_freqanalysis, ft_freqgrandaverage, and ft_freqdescriptives.
To correct for multiple comparisons, one has to specify the field cfg.correctm. This field can have the values ‘no’, ‘max’, ‘cluster’, ‘bonferroni’, ‘holms’, or ‘fdr’. In this tutorial, we only use cfg.correctm = ‘cluster’, which solves the MCP by calculating a so-called cluster-based test statistic and its significance probability.
The calculation of this cluster-based test statistic
- For every sample (a (channel,time)-pair or a (channel,frequency,time)-triplet) the experimental conditions are compared by means of a t-value or some other number that quantifies the effect at this sample. It must be noted that this t-value is not the cluster-based test statistic for which we will calculate the significance probability; it is just an ingredient in the calculation of this cluster-based test statistic. Quantifying the effect at the sample level is possible by means of different measures. These measures are specified in cfg.statistic, which can have the values ‘ft_statfun_indepsamplesT’, ‘ft_statfun_depsamplesT’, ‘ft_statfun_actvsblT’, and many others. We will return to this in the following.
- All samples are selected whose t-value is larger than some threshold as specified in cfg.clusteralpha. It must be noted that the value of cfg.clusteralpha does not affect the false alarm rate of the statistical test; it only sets a threshold for considering a sample as a candidate member of some cluster of samples. If cfg.clusteralpha is equal to 0.05, the t-values are thresholded at the 95-th quantile for a one-sided t-test, and at the 2.5-th and the 97.5-th quantiles for a two-sided t-test.
- Selected samples are clustered in connected sets on the basis of temporal, spatial and spectral adjacency.
- Cluster-level statistics are calculated by taking the sum of the t-values within every cluster.
- The maximum of the cluster-level statistics is taken. This step and the previous one (step 4) are controlled by cfg.clusterstatistic, which can have the values ‘maxsum’, ‘maxsize’, or ‘wcm’. In this tutorial, we will only use ‘maxsum’, which is the default value. The result from step 5 is the test statistic by means of which we evaluate the effect of the experimental conditions.
The calculation of the significance probability
If the MCP is solved by choosing for a cluster-based test statistic (i.e., with cfg.correctm = ‘cluster’), the significance probability can only be calculated by means of the so-called Monte Carlo method. This is because the reference distribution for a permutation test can be approximated (to any degree of accuracy) by means of the Monte Carlo method. In the configuration, the Monte Carlo method is chosen as follows: cfg.method = ‘montecarlo’.
The Monte Carlo significance probability is calculated differently for a within- and between-UO design. We now show how the Monte Carlo significance probability is calculated for in a between-trials experiment (a between-UO design with trials as UO
- Collect the trials of the different experimental conditions in a single set.
- Randomly draw as many trials from this combined data set as there were trials in condition 1 and place them into subset 1. The remaining trials are placed in subset 2. The result of this procedure is called a random partition.
- Calculate the test statistic (i.e., the maximum of the cluster-level summed t-values) on this random partition.
- Repeat steps 2 and 3 a large number of times and construct a histogram of the test statistics. The computation of this Monte Carlo approximation involves a user-specified number of random draws (specified in cfg.numrandomization). The accuracy of the Monte Carlo approximation can be increased by choosing a larger value for cfg.numrandomization.
- From the test statistic that was actually observed and the histogram in step 4, calculate the proportion of random partitions that resulted in a larger test statistic than the observed one. This proportion is the Monte Carlo significance probability, which is also called a p-value.
If the p-value is smaller than the critical alpha-level (typically 0.05) then we conclude that the data in the two experimental conditions are significantly different. This p-value can also be calculated for the second largest cluster-level statistic, the third largest, etc. It is common practice to say that a cluster is significant if its p-value is less than the critical alpha-level. This practice suggests that it is possible to do spatio-spectral-temporal localization by means of the cluster-based permutation test. However, from a statistical perspective, this suggestion is not justified. Consult Maris and Oostenveld, Journal of Neuroscience Methods, 2007 for an elaboration on this topic.
Procedure
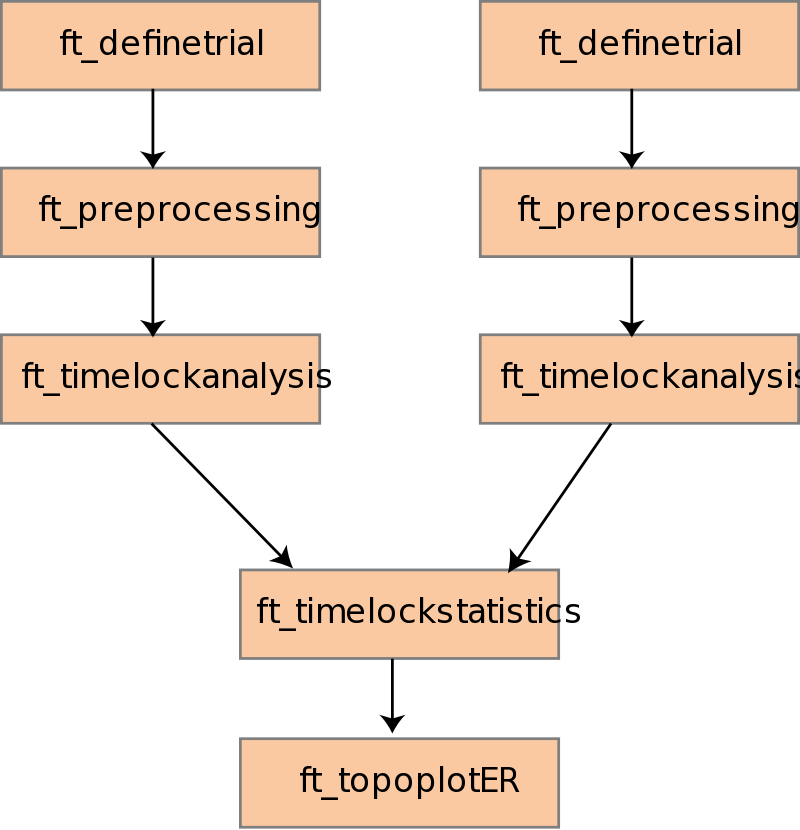
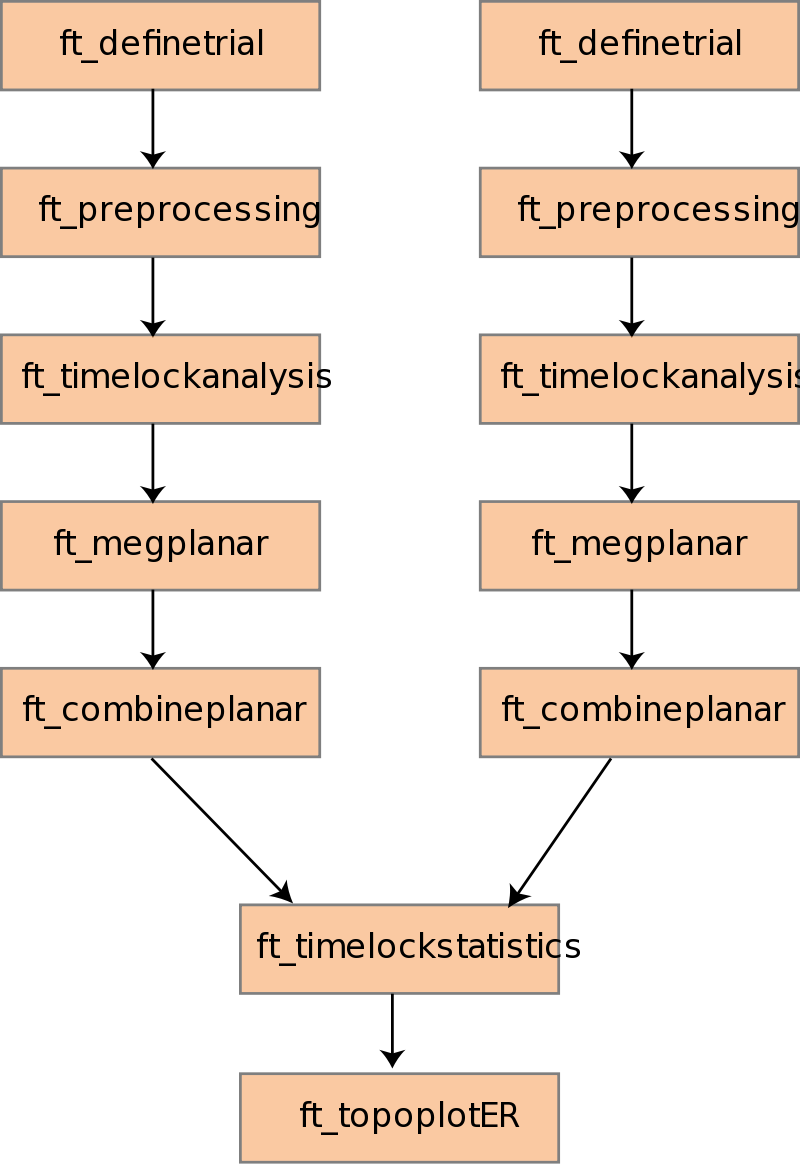
In this tutorial we will consider a between-trials experiment, in which we analyse the data of a single subject. The statistical analysis for this experiment we perform both on axial and planar ERFs. The steps we perform are as follow
- Preprocessing and time-locked analysis with the ft_definetrial, ft_preprocessing and ft_timelockanalysis functions
- (Calculation of the planar gradient with the ft_megplanar and ft_combineplanar functions)
- Permutation test with the ft_timelockstatistics function
- Plotting the result with the ft_topoplotER function
Figure 1. Analysis protocol of a between-trials experiment with axial data
Figure 2. Analysis protocol of a between-trials experiment with planar data
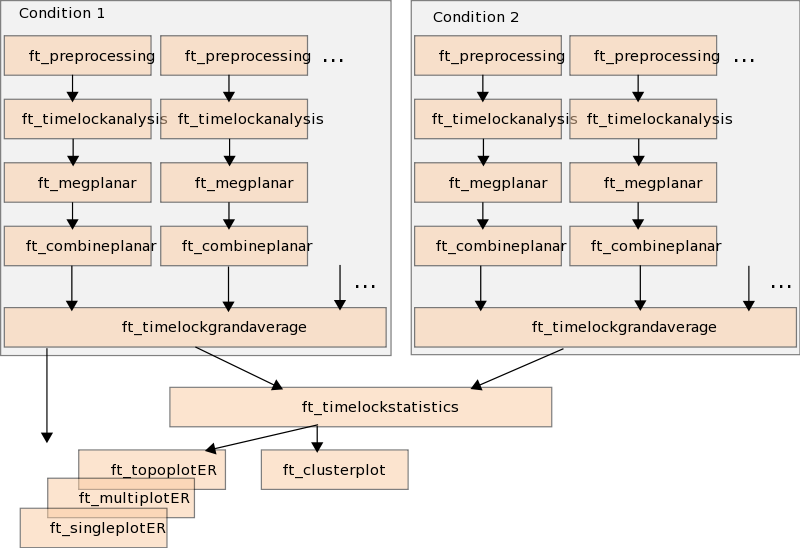
Subsequently, we consider a within-subjects experiment, in which we compare differences between (planar gradient) ERFs over all subjects. The steps we perform are as follow
- Preprocessing and time-locked analysis with ft_definetrial, ft_preprocessing and ft_timelockanalysis functions
- Calculation of the planar gradient with the ft_megplanar and ft_combineplanar functions
- Make grandaverage with the ft_timelockgrandaverage function
- Permutation test with the ft_timelockstatistics function
- Plotting the result with the ft_topoplotER function
Figure 3. Analysis protocol of a within-subjects experiment with planar data
Between-trials experiments
In a between-trials experiment, we analyze the data of a single subject. By means of a statistical test, we want to answer the question whether there is a systematic difference in the MEG recorded on trials with a fully congruent and trials with a fully incongruent sentence ending. (This comparison is the MEG-version of the classical comparison that showed the N400-component in EEG-data).
Preprocessing and time-locked analysis
Reading in the data
We will now read and preprocess the data. If you would like to continue directly with the already preprocessed data, you can download it from dataFIC_LP.mat and dataFC_LP.mat. Load the data into MATLAB with the command load and skip to Permutation test.
Otherwise run the following code:
The ft_definetrial and ft_preprocessing functions require the original MEG dataset, which is available here
Do the trial definition for the all conditions together:
cfg = [];
cfg.dataset = 'Subject01.ds';
cfg.trialfun = 'ft_trialfun_general'; % this is the default
cfg.trialdef.eventtype = 'backpanel trigger';
cfg.trialdef.eventvalue = [3 5 9]; % the values of the stimulus trigger for the three conditions
% 3 = fully incongruent (FIC), 5 = initially congruent (IC), 9 = fully congruent (FC)
cfg.trialdef.prestim = 1; % in seconds
cfg.trialdef.poststim = 2; % in seconds
cfg = ft_definetrial(cfg);
Cleaning
% remove the trials that have artifacts from the trl
cfg.trl([2, 5, 6, 8, 9, 10, 12, 39, 43, 46, 49, 52, 58, 84, 102, 107, 114, 115, 116, 119, 121, 123, 126, 127, 128, 133, 137, 143, 144, 147, 149, 158, 181, 229, 230, 233, 241, 243, 245, 250, 254, 260],:) = [];
% preprocess the data
cfg.channel = {'MEG', '-MLP31', '-MLO12'}; % read all MEG channels except MLP31 and MLO12
cfg.demean = 'yes';
cfg.baselinewindow = [-0.2 0];
cfg.lpfilter = 'yes'; % apply lowpass filter
cfg.lpfreq = 35; % lowpass at 35 Hz.
data_all = ft_preprocessing(cfg);
These data have been cleaned from artifacts by removing several trials and two sensors; see the visual artifact rejection tutorial.
For subsequent analysis we split the data into two different data structures, the fully incongruent condition FIC and the fully congruent condition FC.
cfg = [];
cfg.trials = data_all.trialinfo == 3;
dataFIC_LP = ft_redefinetrial(cfg, data_all);
cfg = [];
cfg.trials = data_all.trialinfo == 9;
dataFC_LP = ft_redefinetrial(cfg, data_all);
Subsequently you can save the data to disk.
save dataFIC_LP dataFIC_LP
save dataFC_LP dataFC_LP
Using the preprocessed data, we now create a data structure that is the average across trials, time-locked to a particular event, using ft_timelockanalysis. The output of ft_timelockanalysis contains an .avg field with the average event-related field, and a .trial field with the individual trial data. The output is stored in timelockFIC and timelockFC for the fully incongruent and the fully congruent condition. This output is then suitable, as well, for statistical analyses.
To obtain the preprocessed data required by ft_timelockanalysis you can get it here from our download server: dataFIC_LP and dataFC_LP.mat.
load dataFIC_LP
load dataFC_LP
cfg = [];
cfg.keeptrials = 'yes';
timelockFIC = ft_timelockanalysis(cfg, dataFIC_LP);
timelockFC = ft_timelockanalysis(cfg, dataFC_LP);
Permutation test
Cluster-level permutation tests for event-related fields are performed by the function ft_timelockstatistics. This function takes as its input arguments a configuration structure cfg and two or more data structures. These data structures must be produced by ft_timelockanalysis or ft_timelockgrandaverage, which all operate on preprocessed data. The argument list of ft_timelockstatistics must contain one data structure for every experimental condition.
The configuration settings
Some fields of the configuration (cfg), such as channel and latency, are not specific for ft_timelockstatistics; their role is similar in other FieldTrip functions. We first concentrate on the fields that are specific for ft_timelockstatistics.
cfg = [];
cfg.method = 'montecarlo'; % use the Monte Carlo Method to calculate the significance probability
cfg.statistic = 'indepsamplesT'; % use the independent samples T-statistic as a measure to
% evaluate the effect at the sample level
cfg.correctm = 'cluster';
cfg.clusteralpha = 0.05; % alpha level of the sample-specific test statistic that
% will be used for thresholding
cfg.clusterstatistic = 'maxsum'; % test statistic that will be evaluated under the
% permutation distribution.
cfg.minnbchan = 2; % minimum number of neighborhood channels that is
% required for a selected sample to be included
% in the clustering algorithm (default=0).
% cfg.neighbours = neighbours; % see below
cfg.tail = 0; % -1, 1 or 0 (default = 0); one-sided or two-sided test
cfg.clustertail = 0;
cfg.alpha = 0.025; % alpha level of the permutation test
cfg.numrandomization = 100; % number of draws from the permutation distribution
n_fc = size(timelockFC.trial, 1);
n_fic = size(timelockFIC.trial, 1);
cfg.design = [ones(1,n_fic), ones(1,n_fc)*2]; % design matrix
cfg.ivar = 1; % number or list with indices indicating the independent variable(s)
We now describe these options one-by-one.
-
With cfg.method = ‘montecarlo’ we choose the Monte Carlo method for calculating the significance probability. This significance probability is a Monte Carlo estimate of the p-value under the permutation distribution.
-
With cfg.statistic = ‘indepsamplesT’, we choose the independent samples T-statistic to evaluate the effect (the difference between the fully congruent and the fully incongruent condition) at the sample level. In cfg.statistic, many other test statistics can be specified. Which test statistic is appropriate depends on your research question and your experimental design. For instance, in a within-UO design, one must use the dependent samples T-statistic (‘ft_statfun_depsamplesT’). And if you want to compare more than two experimental conditions, you should choose an F-statistic (‘ft_statfun_indepsamplesF’ or ‘ft_statfun_depsamplesFmultivariate’). The ‘ft_statfun’ can be omitted in the specification of cfg.statistic, FieldTrip will look for functions on the MATLAB that are named ‘ft_statfun_
' automatically, but it's also OK to specify the full filename, i.e. 'ft_statfun_indepsamplesT'. Also, you can write your own 'statfun' with another test-statistic that you deem relevant. -
We use cfg.clusteralpha to choose the critical value that will be used for thresholding the sample-specific T-statistics. With cfg.clusteralpha = 0.05, every sample-specific T-statistic is compared with the critical value of the univariate T-test with a critical alpha-level of 0.05. (This statistical test would have been the most appropriate test if we had observed a single channel at a single time-point.) The value of cfg.clusteralpha does not affect the false alarm rate of the statistical test at the cluster-level. It is a rational threshold for deciding whether a sample should be considered a member of some large cluster of samples (which may or may not be significant at the cluster-level).
-
We use cfg.clusterstatistic to choose the test statistic that will be evaluated under the permutation distribution. This is the actual test statistic and it must be distinguished from the sample-specific T-statistics that are used for thresholding. With cfg.clusterstatistic = ‘maxsum’, the actual test statistic is the maximum of the cluster-level statistics. A cluster-level statistic is equal to the sum of the sample-specific T-statistics that belong to this cluster. Taking the largest of these cluster-level statistics of the different clusters produces the actual test statistic.
-
The value of cfg.minnbchan is a tuning parameter that determines the way the clusters are formed. More specifically, we use cfg.minnbchan to specify the minimum number of neighbourhood channels that is required for a selected sample (i.e., a sample who’s T-value exceeds the threshold) to be included in the clustering algorithm. With cfg.minnbchan = 0 (the default), it sometimes happens that two clusters are spatially connected via a narrow bridge of samples. Because they are connected, these two clusters are considered as a single cluster. If clusters are interpreted as reflecting spatially distinct sources, such a combined cluster does not make much sense. To suppress this type of combined clusters, one can choose to ignore all selected samples (on the basis of their T-values) if they have less than some minimum number of neighbors that were also selected. This minimum number is assigned to cfg.minnbchan. This number must be chosen independently of the data.
-
cfg.neighbours is a structure that you need to have previously created using ft_prepare_neighbours.
-
We use cfg.tail to choose between a one-sided and a two-sided statistical test. Choosing cfg.tail = 0 affects the calculations in three ways. First, the sample-specific T-values are thresholded from below as well as from above. This implies that both large negative and large positive T-statistics are selected for later clustering. Second, clustering is performed separately for thresholded positive and thresholded negative T-statistics. And third, the critical value for the cluster-level test statistic (determined by cfg.alpha; see further) is now two-sided: negative cluster-level statistics must be compared with the negative critical value, and positive cluster-level statistics must be compared with the positive critical value.
-
We use cfg.alpha to control the false alarm rate of the permutation test (the probability of falsely rejecting the null hypothesis). The value of cfg.alpha determines the critical values with which we must compare the test statistic (i.e., the maximum and the minimum cluster-level statistic). Note that if you want to run a two-sided test, you have to split the critical alpha value by setting cfg.correcttail = ‘alpha’; i.e. this sets cfg.alpha = 0.025, corresponding to a false alarm rate of 0.05 in a two-sided test. The field cfg.alpha is not crucial. This is because the output of ft_timelockstatistics (see further) contains a p-value for every cluster (calculated under the permutation distribution of the maximum/minimum cluster-level statistic). Instead of the critical values, we can also use these p-values to determine the significance of the clusters.
-
We use cfg.numrandomization to control the number of draws from the permutation distribution. Remember that ft_timelockstatistics approximates the permutation distribution by means of a histogram. This histogram is a so-called Monte Carlo approximation of the permutation distribution. This Monte Carlo approximation is used to calculate the p-values and the critical values that are shown in the output of ft_timelockstatistics. In this tutorial, we use cfg.numrandomization = 100. This number is too small for actual applications. As a rule of thumb, use cfg.numrandomization = 500, and double this number if it turns out that the p-value differs from the critical alpha-level (0.05 or 0.01) by less than 0.02.
-
We use cfg.design to store information about the UOs. The content of cfg.design must be a matrix. Consider the hypothetical case that your subject has performed 5 trials in the first condition and 4 trials in the second condition. Then the correct design matrix looks like this: cfg.design = [1 1 1 1 1 2 2 2 2].
-
We use cfg.ivar to indicate the row of the design matrix that contains the independent variable. For a between-trials statistical analysis, the minimum design matrix contains only a single row, and cfg.ivar is superfluous. However, in other statistical analyses (e.g., those for a within-UO design) the design matrix must contain more than one row, and specifying cfg.ivar is essential.
We now briefly discuss the configuration fields that are not specific for ft_timelockstatistics:
cfg_neighb = [];
cfg_neighb.method = 'distance';
neighbours = ft_prepare_neighbours(cfg_neighb, dataFC_LP);
cfg.neighbours = neighbours; % the neighbours specify for each sensor with
% which other sensors it can form clusters
cfg.channel = {'MEG'}; % cell-array with selected channel labels
cfg.latency = [0 1]; % time interval over which the experimental
% conditions must be compared (in seconds)
With these two options, we select the spatio-temporal dataset involving all MEG channels and the time interval between 0 and 1 second. The two experimental conditions will only be compared on this selection of the complete spatio-temporal dataset. Also, feel free to consult our frequently asked questions about ft_prepare_neighbours
One should be aware of the fact that the sensitivity of ft_timelockstatistics (i.e., the probability of detecting an effect) depends on the length of the time interval that is analyzed, as specified in cfg.latency. For instance, assume that the difference between the two experimental conditions extends over a short time interval only (e.g., between 0.3 and 0.4 sec.). If it is known in advance that this short time interval is the only interval where an effect is likely to occur, then one should limit the analysis to this time interval (i.e., choose cfg.latency = [0.3 0.4]). Choosing a time interval on the basis of prior information about the time course of the effect will increase the sensitivity of the statistical test. If there is no prior information, then one must compare the experimental conditions over the complete time interval. This is accomplished by choosing cfg.latency = ‘all’. In this tutorial, we choose cfg.latency = [0 1] because EEG-studies have shown that the strongest effect of semantic incongruity is observed in the first second after stimulus presentation.
Now, run ft_timelockstatistics to compare timelockFIC and timelockFC using the configuration described above.
[stat] = ft_timelockstatistics(cfg, timelockFIC, timelockFC);
Save the output to disk:
save stat_ERF_axial_FICvsFC stat;
The format of the output
The output can also be obtained from stat_ERF_axial_FICvsFC.mat. If you need to reload the statistics output, use:
load stat_ERF_axial_FICvsFC
The output of ft_timelockstatistics has separate fields for positive and negative clusters. For the positive clusters, the output is given in the following pair of fields: stat.posclusters and stat.posclusterslabelmat. The field stat.posclusters is an array that provides the following information for every cluster:
-
The field clusterstat contains the cluster-level test statistic (here: the sum of the T-values in this cluster).
-
The field prob contains the proportion of draws from the permutation distribution with a maximum cluster-level statistic that is larger than the cluster-level test statistic. The elements in the array stat.posclusters are sorted according to these probabilities: the cluster with the smallest p-value comes first, followed by the cluster with the second-smallest, etc. Thus, if the k-th cluster has a p-value that is larger than the critical alpha-level (e.g., 0.025), then so does the (k+1)-th. Type stat.posclusters(k) on the MATLAB command line to see the information for the k-th cluster. Note, however, that in fact for the statistical inferential decision (i.e. reject or not the null hypothesis), only the p-value of the largest cluster is relevant. Therefore, importantly, it is a bit silly to use the terminology ‘significant clusters’ in this context, by evaluating the cluster-associated p-values.
The field stat.posclusterslabelmat is a spatiotemporal matrix. This matrix contains numbers that identify the clusters to which the (channel,time)-pairs (the samples) belong. For example, all (channel,time)-pairs that belong to the third cluster, are identified by the number 3. As will be shown in the following, this information can be used to visualize the topography of the clusters.
For the negative clusters, the output is given in the following pair of fields: stat.negclusters and stat.negclusterslabelmat. These fields contain the same type of information as stat.posclusters and stat.posclusterslabelmat, but now for the negative clusters.
By inspecting stat.posclusters and stat.negclusters, it can be seen that only the first positive and the first negative cluster have a p-value less than the critical alpha-level of 0.025. This critical alpha-level corresponds to a false alarm rate of 0.05 in a two-sided test. By typing stat.posclusters(1) on the MATLAB command line, you should obtain more or less the following:
stat.posclusters(1)
ans =
prob: 0.0099
clusterstat: 8.2721e+03
stddev: 0.0099
cirange: 0.0194
And by typing stat.negclusters(1), you should obtain more or less the following:
stat.negclusters(1)
ans =
prob: 0.0099
clusterstat: -1.0251e+04
stddev: 0.0099
cirange: 0.0194
It is possible that the p-values in your output are a little bit different from 0. This is because ft_timelockstatistics calculated as a Monte Carlo approximation of the permutation p-values: the p-value for the k-th positive cluster is calculated as the proportion of random draws from the permutation distribution in which the maximum of the cluster-level statistics is larger than stat.posclusters(k).clusterstat. Also, given the Monte Carlo approximation, the probability values are not exact, and their confidence interval and standard deviation are given by the cirange, and stddev, respectively.
Plotting of the results
To plot the results of the permutation test, we use the plotting function ft_topoplotER. In doing so, we will plot a topography of the difference between the two experimental conditions (FIC and FC). On top of that, and for each timestep of interest, we will highlight the sensors which are members of significant clusters. First, however, we must calculate the difference between conditions using ft_math.
cfg = [];
avgFIC = ft_timelockanalysis(cfg, dataFIC_LP);
avgFC = ft_timelockanalysis(cfg, dataFC_LP);
% Then take the difference of the averages using ft_math
cfg = [];
cfg.operation = 'subtract';
cfg.parameter = 'avg';
raweffectFICvsFC = ft_math(cfg, avgFIC, avgFC);
We then construct a boolean matrix indicating whether a channel/time point belongs to a cluster that we deem interesting to inspect. This matrix has size [Number_of_MEG_channels x Number_of_time_samples], like stat.posclusterslabelmat. We’ll make two such matrices: one for positive clusters (named pos), and one for negative (neg). All (channel,time)-pairs belonging to the large clusters whose probability of occurrence is sufficiently low in relation to the associated randomization distribution of clusterstats will be coded in the new boolean matrix as 1, and all those that don’t will be coded as 0.
% Make a vector of all p-values associated with the clusters from ft_timelockstatistics.
pos_cluster_pvals = [stat.posclusters(:).prob];
% Then, find which clusters are deemed interesting to visualize, here we use a cutoff criterion based on the
% cluster-associated p-value, and take a 5% two-sided cutoff (i.e. 0.025 for the positive and negative clusters,
% respectively
pos_clust = find(pos_cluster_pvals < 0.025);
pos = ismember(stat.posclusterslabelmat, pos_clust);
% and now for the negative clusters...
neg_cluster_pvals = [stat.negclusters(:).prob];
neg_clust = find(neg_cluster_pvals < 0.025);
neg = ismember(stat.negclusterslabelmat, neg_clust);
Alternatively, we can manually select which clusters we want to plot. If we only want to see the extent of the first (i.e. most significant) positive and negative clusters, for instance, we can do so as follows:
pos = stat.posclusterslabelmat == 1; % or == 2, or 3, etc.
neg = stat.negclusterslabelmat == 1;
To plot a sequence of twenty topographic plots equally spaced between 0 and 1 second, we define the vector j of time steps. These time intervals correspond to the samples m in stat and in the variables pos. and neg. m and j must, therefore, have the same length.
To be sure that your sample-based time windows align with your time windows in seconds, check the following:
timestep = 0.05; % timestep between time windows for each subplot (in seconds)
sampling_rate = dataFC_LP.fsample; % Data has a temporal resolution of 300 Hz
sample_count = length(stat.time);
% number of temporal samples in the statistics object
j = [0:timestep:1]; % Temporal endpoints (in seconds) of the ERP average computed in each subplot
m = [1:timestep*sampling_rate:sample_count]; % temporal endpoints in M/EEG samples
To plot the data use the following for-loop:
% First ensure the channels to have the same order in the average and in the statistical output.
% This might not be the case, because ft_math might shuffle the order
[i1,i2] = match_str(raweffectFICvsFC.label, stat.label);
for k = 1:20
subplot(4,5,k);
cfg = [];
cfg.xlim = [j(k) j(k+1)]; % time interval of the subplot
cfg.zlim = [-2.5e-13 2.5e-13];
% If a channel is in a to-be-plotted cluster, then
% the element of pos_int with an index equal to that channel
% number will be set to 1 (otherwise 0).
% Next, check which channels are in the clusters over the
% entire time interval of interest.
pos_int = zeros(numel(raweffectFICvsFC.label),1);
neg_int = zeros(numel(raweffectFICvsFC.label),1);
pos_int(i1) = all(pos(i2, m(k):m(k+1)), 2);
neg_int(i1) = all(neg(i2, m(k):m(k+1)), 2);
cfg.highlight = 'on';
% Get the index of the to-be-highlighted channel
cfg.highlightchannel = find(pos_int | neg_int);
cfg.comment = 'xlim';
cfg.commentpos = 'title';
cfg.layout = 'CTF151_helmet.mat';
cfg.interactive = 'no';
cfg.figure = 'gca'; % plots in the current axes, here in a subplot
ft_topoplotER(cfg, raweffectFICvsFC);
end
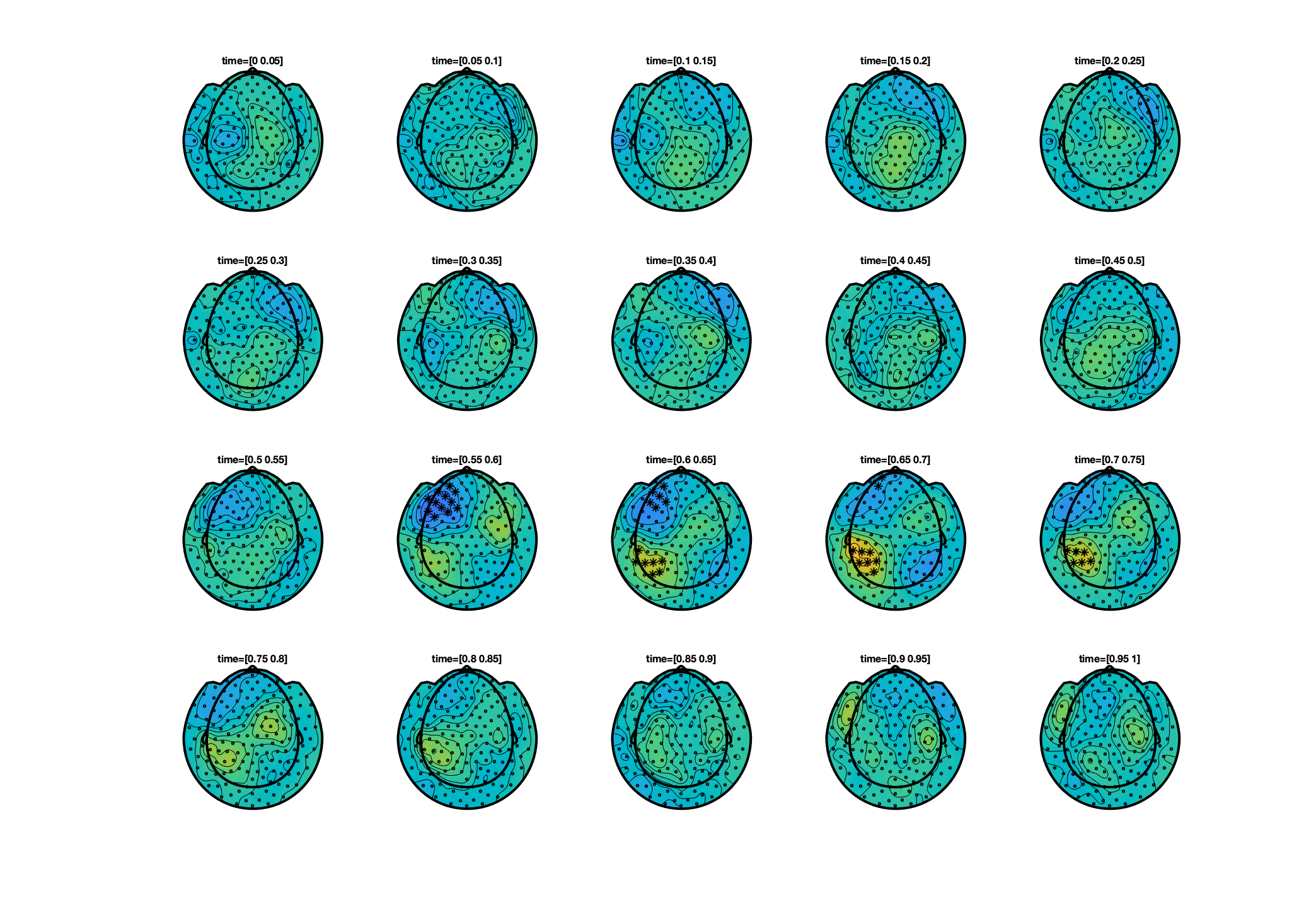
In this for-loop, cfg.xlim defines the time interval of each subplot. The variables pos_int and neg_int boolean vectors indicating which channels of pos and neg are significant in the time interval of interest. This is defined in cfg.highlightchannel. The for-loop plots 20 subplots covering a time interval of 50 ms each. Running this for-loop creates the following figure:
Figure 4: Raw effect (FIC-FC) on the ERFs of subject 1, significant clusters are highlighted..
Using planar gradient data
To perform the permutation test using synthetic planar gradient data, the data must first be converted using the functions ft_megplanar and ft_combineplanar. These functions were described in the tutorial on event-related fields. After running these functions, the statistical analysis using ft_timelockstatistics involves the same configuration options as for ordinary event-related averages (no synthetic planar gradients). There is only one additional step, which is needed to add the gradiometer structure to one of the planar gradient data sets.
cfg = [];
cfg.planarmethod = 'sincos';
cfg.neighbours = neighbours; % also here, neighbouring sensors needs to be defined
timelockFIC_planar = ft_megplanar(cfg, timelockFIC);
timelockFC_planar = ft_megplanar(cfg, timelockFC);
timelockFIC_planar_cmb = ft_combineplanar(cfg, timelockFIC_planar);
timelockFC_planar_cmb = ft_combineplanar(cfg, timelockFC_planar);
timelockFIC_planar_cmb.grad = timelockFIC.grad; % add the gradiometer structure
timelockFC_planar_cmb.grad = timelockFC.grad;
Having calculated synthetic planar gradient data, one can use the same configuration parameters as used for the analysis of the original data.
cfg = [];
cfg.channel = {'MEG'};
cfg.latency = [0 1];
cfg.neighbours = neighbours;
cfg.method = 'montecarlo';
cfg.statistic = 'indepsamplesT';
cfg.correctm = 'cluster';
cfg.clusteralpha = 0.05;
cfg.clusterstatistic = 'maxsum';
cfg.minnbchan = 2;
cfg.tail = 0;
cfg.clustertail = 0;
cfg.alpha = 0.025;
cfg.numrandomization = 100;
n_fc = size(timelockFC_planar_cmb.trial, 1);
n_fic = size(timelockFIC_planar_cmb.trial, 1);
cfg.design = [ones(1,n_fic), ones(1,n_fc)*2]; % design matrix
cfg.ivar = 1; % number or list with indices indicating the independent variable(s)
[stat] = ft_timelockstatistics(cfg, timelockFIC_planar_cmb, timelockFC_planar_cmb)
save stat_ERF_planar_FICvsFC stat
The output can also be obtained from here. If you need to reload the statistics output, use:
load stat_ERF_planar_FICvsFC
We now calculate the raw effect in the average with planar gradient data using the following configuration:
cfg = [];
cfg.keeptrials = 'no'; % now only the average, not the single trials
avgFIC_planar = ft_timelockanalysis(cfg, timelockFIC_planar);
avgFC_planar = ft_timelockanalysis(cfg, timelockFC_planar);
cfg = [];
avgFIC_planar_cmb = ft_combineplanar(cfg, avgFIC_planar);
avgFC_planar_cmb = ft_combineplanar(cfg, avgFC_planar);
% subtract avgFC from avgFIC
cfg = [];
cfg.operation = 'subtract'
cfg.parameter = 'avg';
raweffectFICvsFC = ft_math(cfg, avgFIC_planar_cmb, avgFC_planar_cmb);
Using the following configuration for ft_topoplotER we can plot the raw effect and highlight the channels contributing to the largest cluster
figure;
timestep = 0.05; %(in seconds)
sampling_rate = dataFC_LP.fsample;
sample_count = length(stat.time);
j = [0:timestep:1]; % Temporal endpoints (in seconds) of the ERP average computed in each subplot
m = [1:timestep*sampling_rate:sample_count]; % temporal endpoints in M/EEG samples
pos_cluster_pvals = [stat.posclusters(:).prob];
pos_clust = find(pos_cluster_pvals < 0.025);
pos = ismember(stat.posclusterslabelmat, pos_clust);
% Remember to do the same for negative clusters if you want them!
% First ensure the channels to have the same order in the average and in the statistical output.
% This might not be the case, because ft_math might shuffle the order
[i1,i2] = match_str(raweffectFICvsFC.label, stat.label);
for k = 1:20;
subplot(4,5,k);
cfg = [];
cfg.xlim = [j(k) j(k+1)];
cfg.zlim = [-1.0e-13 1.0e-13];
pos_int = zeros(numel(raweffectFICvsFC.label),1);
pos_int(i1) = all(pos(i2, m(k):m(k+1)), 2);
cfg.highlight = 'on';
cfg.highlightchannel = find(pos_int);
cfg.comment = 'xlim';
cfg.commentpos = 'title';
cfg.layout = 'CTF151_helmet.mat';
cfg.figure = 'gca';
ft_topoplotER(cfg, raweffectFICvsFC);
end
Figure 5: Raw effect (FIC-FC) on the planar gradient ERFs of subject 1, the most prominent clusters are highlighted..
Within-subjects experiments
We now consider experiments involving multiple subjects that are each observed in multiple experimental conditions. Typically, every subject is observed in a large number of trials, each one belonging to one experimental condition. Usually, for every subject, averages are computed over all trials belonging to each of the experimental conditions. Thus, for every subject, the data are summarized in an array of condition-specific averages. The permutation test that is described in this section informs us about the following null hypothesis: the probability distribution of the condition-specific averages is independent of the experimental conditions.
Reading-in, preprocessing, timelockanalysis, planar gradient, and grandaveraging
We now describe how we can statistically test the difference between the event-related averages for fully incongruent (FIC) and the fully congruent (FC) sentence endings. For this analysis we use planar gradient data. For convenience we will not do the reading-in and preprocessing steps on all subjects. Instead we begin by loading the timelock structures containing the event-related averages (of the planar gradient data) of all ten subjects. The data is available from ERF_orig.mat.
load ERF_orig
ERF_orig contains allsubjFIC and allsubjFC, each storing the event-related averages for the fully incongruent, and the fully congruent sentence endings, respectively.
The format for these variables, are a prime example of how you should organise your data to be suitable for ft_XXXstatistics. Specifically, each variable is a cell-array of structures, with each subject’s averaged stored in one cell. To create this data structure two steps are required. First, the single-subject averages were calculated individually for each subject using the function ft_timelockanalysis. Second, using a for-loop we have combined the data from each subject, within each condition, into one variable (allsubj_FIC/allsubj_FC). We suggest that you adopt this procedure as well.
On a technical note, it is preferred to represent the multi-subject data as a cell-array of structures, rather than a so-called struct-array. The reason for this is that the cell-array representation allows for easy expansion into a MATLAB function that allows for a variable number of input arguments (which is how the ft_XXXstatistics functions have been designed).
Permutation test
We now perform the permutation test using ft_timelockstatistics. The configuration settings for this analysis differ from the previous settings in several fields:
- We have to select a different measure to evaluate the effect at sample level (in cfg.statistic)
- The design matrix is different (i.c., it now contains two lines instead of one)
- The so-called unit variable has to be defined.
The configuration looks as follows:
cfg = [];
cfg.channel = {'MEG'};
cfg.latency = [0 1];
cfg.method = 'montecarlo';
cfg.statistic = 'depsamplesT';
cfg.correctm = 'cluster';
cfg.clusteralpha = 0.05;
cfg.clusterstatistic = 'maxsum';
cfg.minnbchan = 2;
cfg.neighbours = neighbours; % same as defined for the between-trials experiment
cfg.tail = 0;
cfg.clustertail = 0;
cfg.alpha = 0.025;
cfg.numrandomization = 500;
Nsubj = 10;
design = zeros(2, Nsubj*2);
design(1,:) = [1:Nsubj 1:Nsubj];
design(2,:) = [ones(1,Nsubj) ones(1,Nsubj)*2];
cfg.design = design;
cfg.uvar = 1;
cfg.ivar = 2;
We now describe the differences between this configuration and the configuration for a between-trials experiment.
-
Instead of an independent samples T-statistic, we use the dependent samples T-statistic to evaluate the effect at the sample level (cfg.statistic = ‘depsamplesT’). This is because we are dealing with a within-UO instead of a between-UO design.
-
The design matrix in a within-UO design is different from the design matrix in a between-UO design. In the design matrix for a within-UO design, you have to specify the unit variable. The unit variable specifies the units that have produced the different condition-specific data structures. For example, consider a hypothetical study with 4 subjects and 2 experimental conditions. The design matrix may then look like this: design = [1 2 3 4 1 2 3 4; 1 1 1 1 2 2 2 2 ]. The first row of this matrix is the unit variable: it specifies that the first subject produced the first and the fifth data structure, the second subject produced the second and the sixth data structure, etc. The second row of the design matrix is the independent variable.
-
Because the design matrix contains both a unit variable and an independent variable, it has to be specified in the configuration which row contains which variable. This information is passed in the fields cfg.uvar (for the unit variable) and cfg.ivar (for the independent variable).
Now, use the configuration above to perform the following statistical analysis:
[stat] = ft_timelockstatistics(cfg, allsubjFIC{:}, allsubjFC{:})
save stat_ERF_planar_FICvsFC_GA stat
The output can also be obtained from stat_ERF_planar_FICvsFC_GA.mat. If you need to reload the statistics output, use:
load stat_ERF_planar_FICvsFC_GA
From inspection of stat.posclusters and stat.negclusters, we observe that there is only one significant positive cluster and no significant negative cluster.
Plotting the results
For plotting we first use ft_timelockgrandaverage to calculate the grand average (average across all subject’s average).
% load individual subject data
load('ERF_orig');
% calculate the grand average for each condition
cfg = [];
cfg.channel = 'all';
cfg.latency = 'all';
cfg.parameter = 'avg';
GA_FIC = ft_timelockgrandaverage(cfg, allsubjFIC{:});
GA_FC = ft_timelockgrandaverage(cfg, allsubjFC{:});
% "{:}" means to use data from all elements of the variable
With the output, we can now create the plots
cfg = [];
cfg.operation = 'subtract';
cfg.parameter = 'avg';
GA_FICvsFC = ft_math(cfg, GA_FIC, GA_FC);
figure;
% define parameters for plotting
timestep = 0.05; %(in seconds)
sampling_rate = dataFIC_LP.fsample;
sample_count = length(stat.time);
j = [0:timestep:1]; % Temporal endpoints (in seconds) of the ERP average computed in each subplot
m = [1:timestep*sampling_rate:sample_count]; % temporal endpoints in M/EEG samples
% get relevant values
pos_cluster_pvals = [stat.posclusters(:).prob];
pos_clust = find(pos_cluster_pvals < 0.025);
pos = ismember(stat.posclusterslabelmat, pos_clust);
% First ensure the channels to have the same order in the average and in the statistical output.
% This might not be the case, because ft_math might shuffle the order
[i1,i2] = match_str(GA_FICvsFC.label, stat.label);
% plot
for k = 1:20;
cfg.figure = subplot(4,5,k);
cfg.xlim = [j(k) j(k+1)];
cfg.zlim = [-5e-14 5e-14];
pos_int = zeros(numel(GA_FICvsFC.label),1);
pos_int(i1) = all(pos(i2, m(k):m(k+1)), 2);
cfg.highlight = 'on';
cfg.highlightchannel = find(pos_int);
cfg.comment = 'xlim';
cfg.commentpos = 'title';
cfg.layout = 'CTF151_helmet.mat';
cfg.figure = 'gca';
ft_topoplotER(cfg, GA_FICvsFC);
end
Figure 6: Raw effect (FIC-FC) on the grand average planar gradient ERFs with the prominent clusters highlighted.
Summary and suggested further reading
In this tutorial, it was shown how to do non-parametric statistics on axial and planar ERFs in a between-trials and in within-subjects design. It was also shown how to plot the results.
If you are interested in parametric tests in FieldTrip, you can read the Parametric and non-parametric statistics on event-related fields tutorial. If you are interested in how to do the same statistics on time-frequency representations, you can read the Cluster-based permutation tests on time-frequency data tutorial.
If you would like to read more about statistical analysis, you can look at the following FAQs:
- How can I define neighbouring sensors?
- How can I determine the onset of an effect?
- How to test an interaction effect using cluster-based permutation tests?
- How can I test for correlations between neuronal data and quantitative stimulus and behavioral variables?
- How can I test whether a behavioral measure is phasic?
- How can I use the ivar, uvar, wvar and cvar options to precisely control the permutations?
- How does a difference in trial numbers per condition affect my statistical test
- How does ft_prepare_neighbours work?
- How NOT to interpret results from a cluster-based permutation test
- Should I use t or F values for cluster-based permutation tests?
- What is the idea behind statistical inference at the second-level?
- Why should I use the cfg.correcttail option when using statistics_montecarlo?
- How can I define neighbouring sensors?
- How does ft_prepare_neighbours work?
- What is the idea behind statistical inference at the second-level?
- Why should I use the cfg.correcttail option when using statistics_montecarlo?
and example scripts:
- Apply non-parametric statistics with clustering on TFRs of power that were computed with BESA
- Computing and reporting the effect size
- Using General Linear Modeling on time series data
- Using General Linear Modeling over trials
- Defining electrodes as neighbours for cluster-level statistics
- Using GLM to analyze NIRS timeseries data
- Using simulations to estimate the sample size for cluster-based permutation test
- Source statistics
- Stratify the distribution of one variable that differs in two conditions
- Using threshold-free cluster enhancement for cluster statistics
- Use simulated ERPs to explore cluster statistics
- Apply non-parametric statistics with clustering on TFRs of power that were computed with BESA
- Computing and reporting the effect size
- Defining electrodes as neighbours for cluster-level statistics
- Using simulations to estimate the sample size for cluster-based permutation test
- Use simulated ERPs to explore cluster statistics